Задание Windows Forms Application 2 Решение дифференциального уравнения методом Рунге-Кутта Постановка задачи и варианты задания

Решить численно дифференциальное уравнение первого порядка методом Рунге-Кутта с шагом при начальном условии. Решение представить в виде таблицы, содержащей номер№ точки (51 точка) и значенияв этих точках. Построить график функции и ее производной.

Варианты задания

№	Дифференциальное уравнение
1		-0,5	0,2
2		-0,2	0,1
3		-0,5	0,7
4		-0,3	0
5		-0,4	0,3
6		-0,4	0
7		-0,2	0
8		-0,4	0
9		0,4	1
10		-0,7	-4
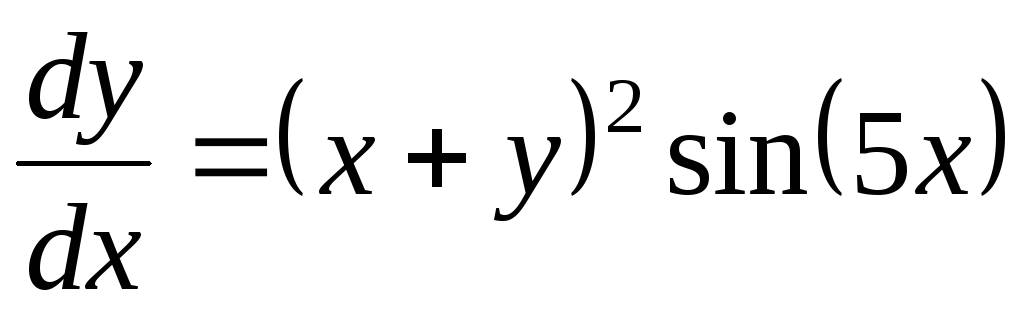
11		-0,3	-3
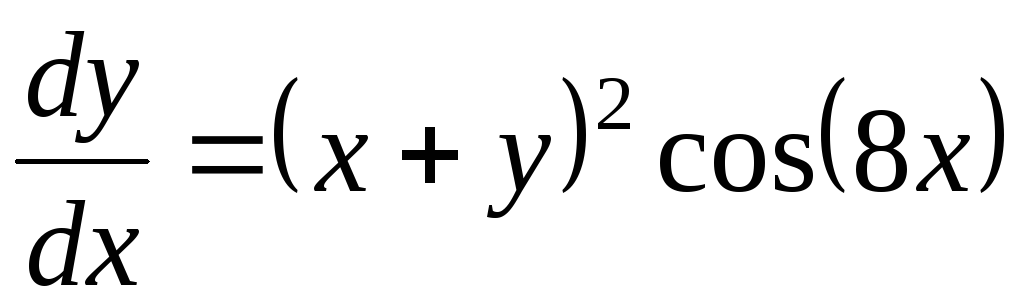
12		-0,6	1,5
13		-0,1	0,2
14		0,6	4,5
15		-0,9	1,9

Описание метода Рунге-Кутта

Метод Рунге-Кутта является методом повышенной точности для численного решения дифференциальных уравнений с заданными начальными условиями. Пусть на отрезке требуется найти решение дифференциального уравнения

(1)

с начальным условием . Разобьем отрезокнаравных частей точками, где- шаг интегрирования. Каждое следующее значение функцииопределяется через предыдущее по алгоритму

. (2)

Приращение вычисляется по формуле

, (3)

где

(4)

Алгоритм стартует со значения . Коэффициенты обновляются на каждом шаге интегрирования.

Предварительная оценка погрешности делается после двойного просчета по формуле:

;

где– точное решение в точке;– приближенные значения, полученные с шагомисоответственно. Шагвыбирают так, чтобы выполнялось условие, где– заданная точность.

Метод Рунге-Кутта может быть применен к решению уравнений более высокого порядка путем сведения их к системе дифференциальных уравнений первого порядка. Также возможно решение системы дифференциальных уравнений.

Геометрическая интерпретация коэффициентов .

Пусть кривая (рис.1) есть решение дифференциального уравнения (1) на отрезке. Точкаданной кривой лежит на прямой, параллельной осии делит отрезокпополам,и– точки пересечения касательной, проведенной к кривойв точке, с ординатамии. Тогда числос точностью до множителяесть угловой коэффициент касательной к кривойв точке:

.

Точка имеет координаты. Следовательно,с точностью до множителяесть угловой коэффициент касательной, проведенной в точке(– отрезок касательной): .

Через точку проведем прямую, параллельную отрезку, до пересечения в точкес вертикалью. Тогда точкаимеет координаты, а с точностью до множителяесть угловой коэффициент касательной, проведенной к интегральной кривой в точке: (– отрезок этой касательной).

Через точку проведем прямую, параллельную отрезку, которая пересечет вертикаль в конце шага в точкес координатами. Тогдас точностью до множителяопределяет угловой коэффициент касательной, проведенной к интегральной кривой в точке:. Таким образом, расчетное значениесвязано с угламисоотношением

.