Лекция 3. Скалярное умножение свободных векторов §8. Проекция вектора на вектор

О п р е д е л е н и е. Единичным вектором или ортом называется вектор, длина которого равна 1.

Если , то вектор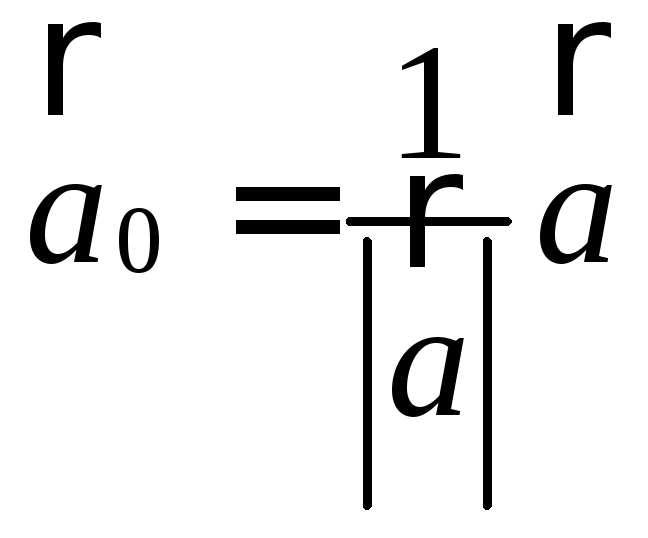является ортом вектора.

О п р е д е л е н и е. Проекцией точки на прямую называется точка пересечения этой прямой с перпендикулярной ей плоскостью , проходящей через точку:.

О п р е д е л е н и е. Векторной проекцией вектора на ненулевой вектор называется вектор , гдеи– проекции точекина прямую, параллельную вектору(обознач.).

Можно показать, что векторная проекция вектора на вектор не зависит от выбора представителя этого вектора.

Так как , где– орт вектора, то. Числоназываетсяскалярной проекцией вектора на вектор.

Таким образом, и.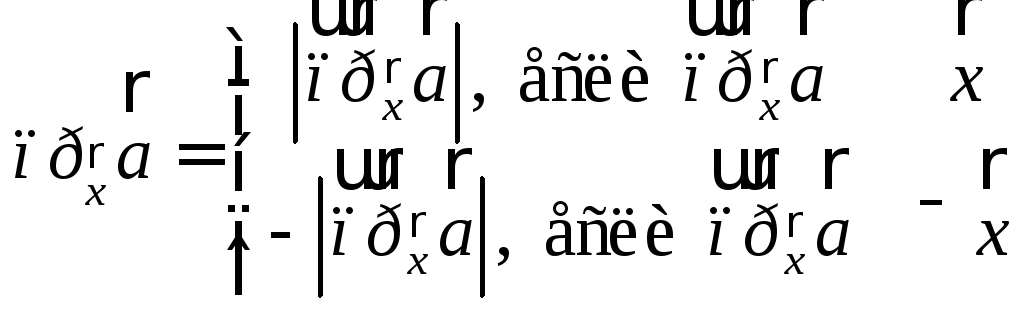

Отметим, что при определении векторной и скалярной проекций важно только направление ненулевого вектора , его длина не является существенной. Таким образом, если, тои.

Можно обосновать следующие свойства векторных проекций:

1. ;

2. .

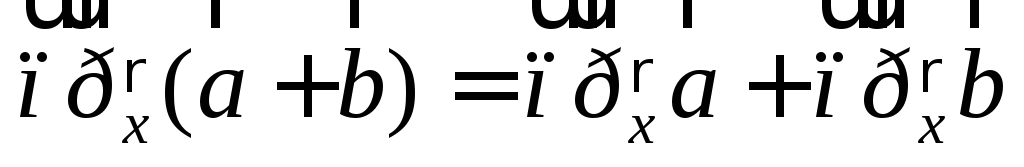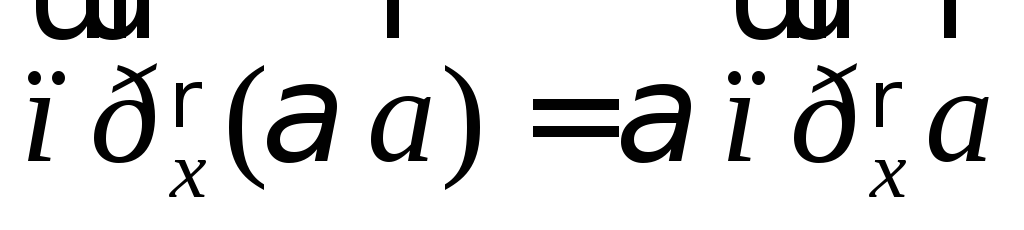Выразив векторные проекции через орт вектора , из свойств векторных проекций получимсвойства скалярных проекций:

1. ;

2. .

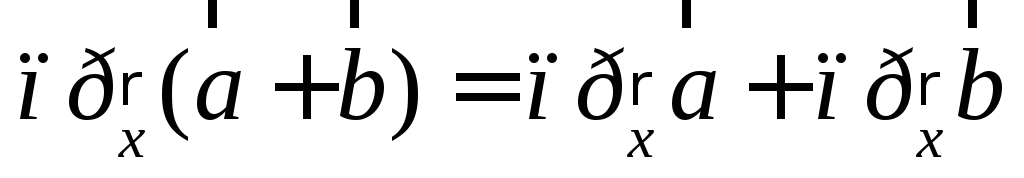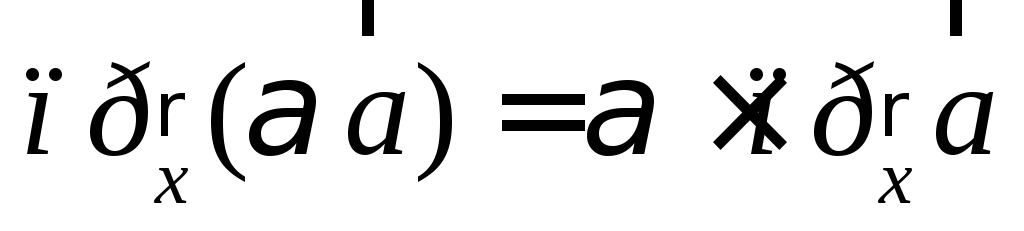О п р е д е л е н и е. Углом между ненулевыми свободными векторами иназывается величина угла, не превосходящего развернутый угол, где,.

Таким образом, чтобы увидеть угол между ненулевыми свободными векторами, нужно отложить их от одной точки.

Если один из векторов нулевой, то угол между векторами не определен, можно считать его любым, не превосходящим развернутый угол. Тогда получим, что угол между векторами может принимать значения от 0 до .

Рассмотрев возможные значения угла между ненулевыми векторамии(;;;), получимеще одно свойство скалярных проекций:

3. .

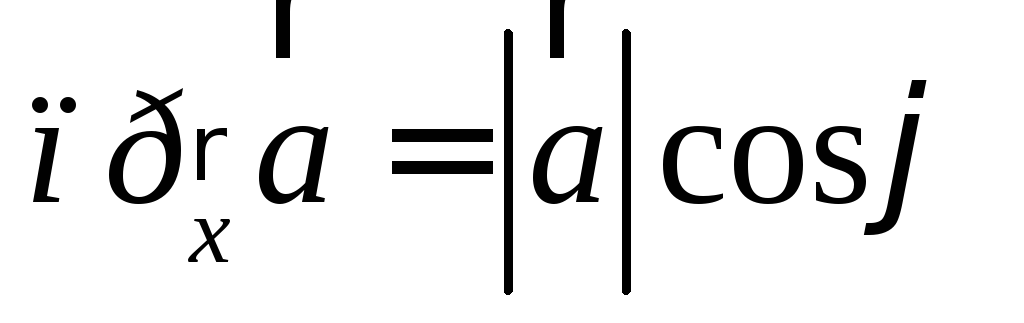§9. Скалярное умножение свободных векторов

О п р е д е л е н и е. Скалярным произведением векторов иназывается число, равное произведению длин этих векторов и косинуса угла между ними:.

О п р е д е л е н и е. Векторы, скалярное произведение которых равно нулю называются ортогональными.

Для обозначения ортогональности векторов используют знак .

Очевидны свойства скалярного умножения свободных векторов:

1. ;

2. ;

3. ;

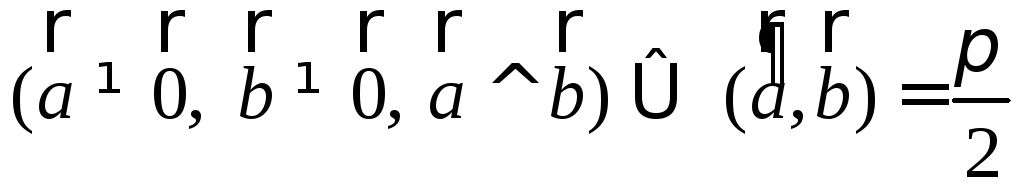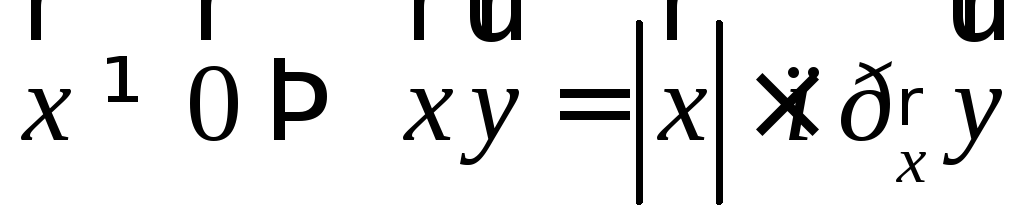У п р а ж н е н и е. Используя свойства скалярного умножения и свойства скалярных проекций доказать законы скалярного умножения:

1. ;

2. ;

3. ;

4. .

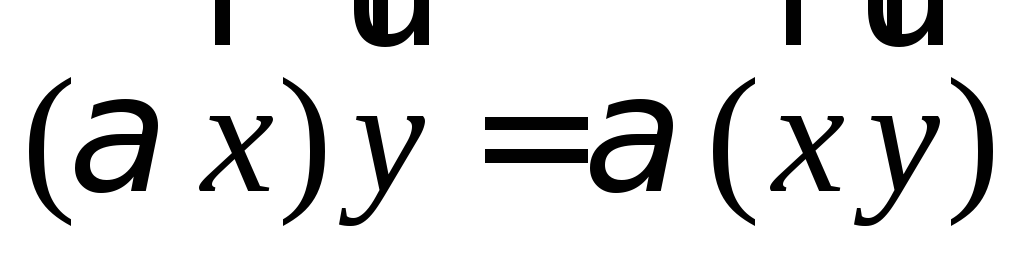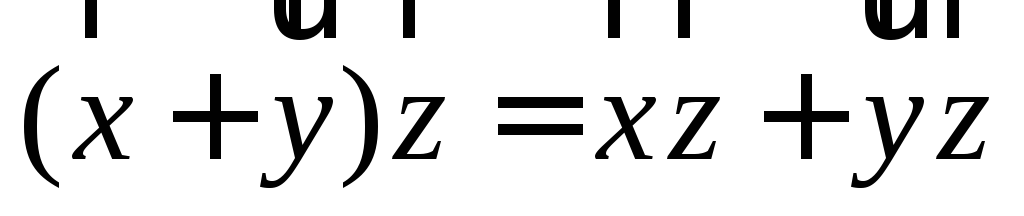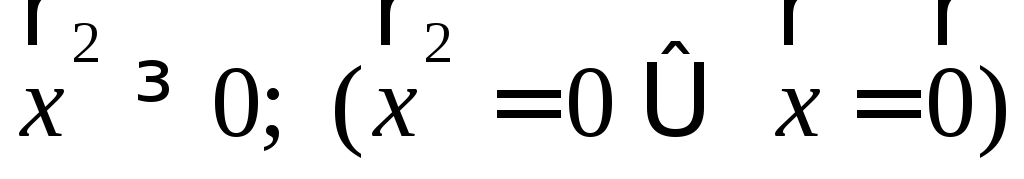Базис , состоящий из единичных, попарно ортогональных векторов, называетсяортонормированным базисом.

У п р а ж н е н и е. Вывести формулы вычисления скалярного произведения векторов и длины вектора через координаты в ортонормированном базисе:

; .

Основные приложения скалярного умножения векторов:

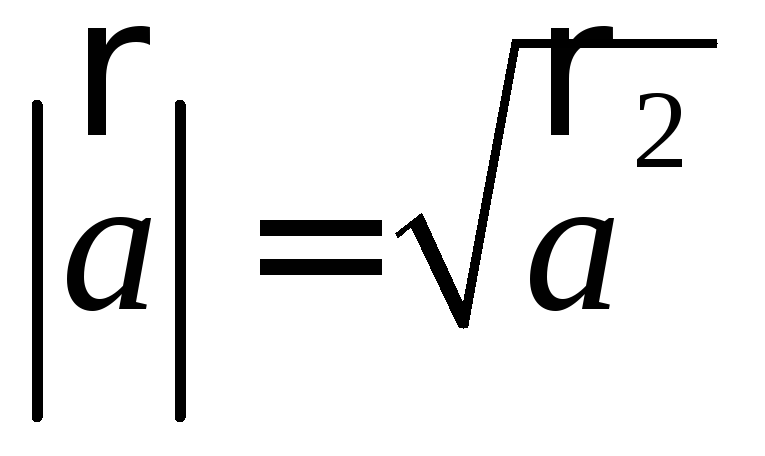1. –длина вектора равна корню квадратному из скалярного квадрата этого вектора;

2. ;

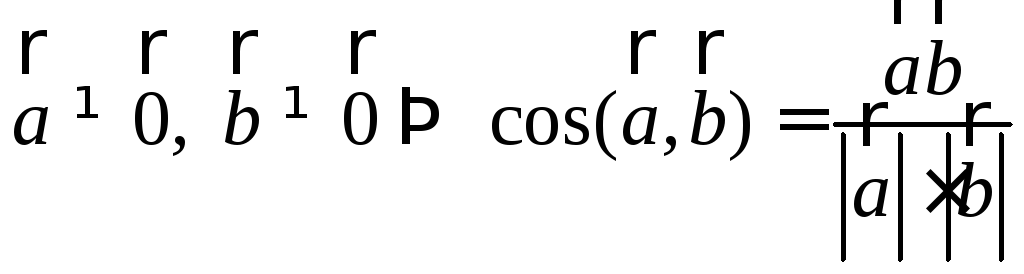3. Угол между векторам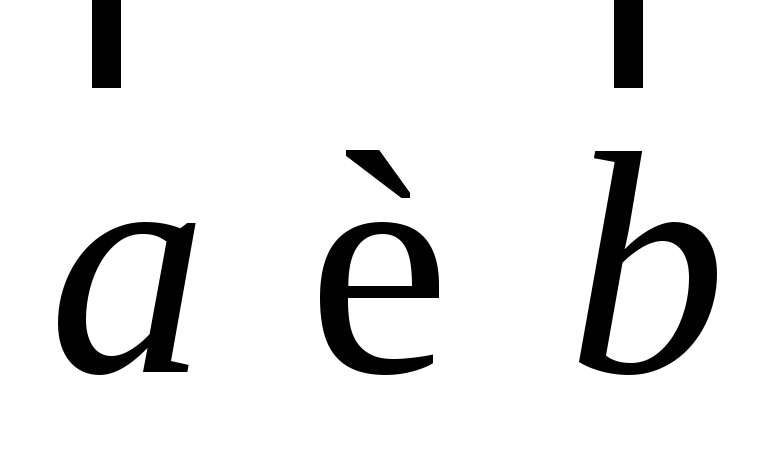и : остры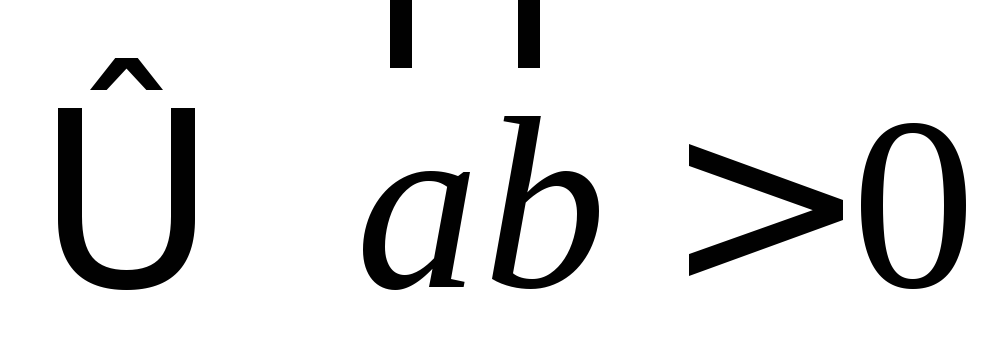й; тупой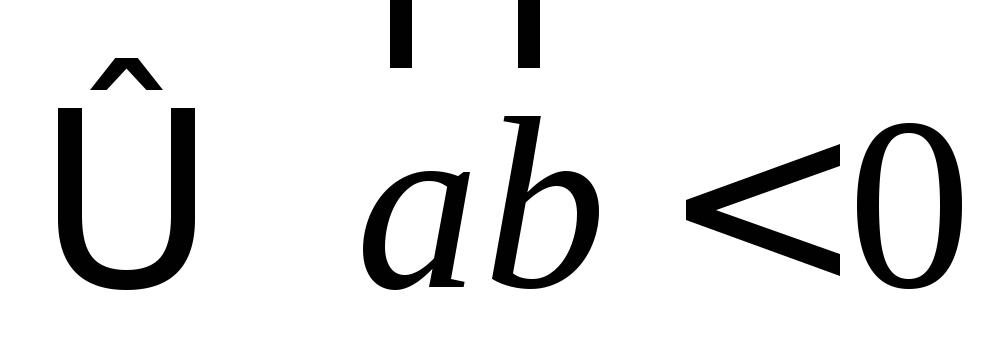. Векторы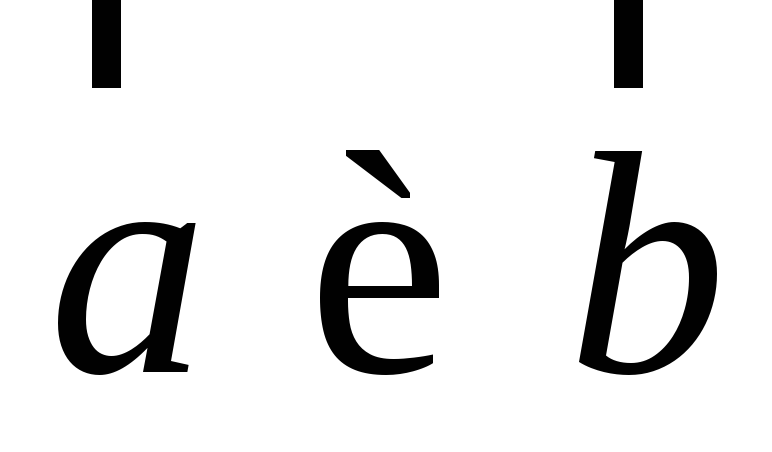ортогональны.

4. ;

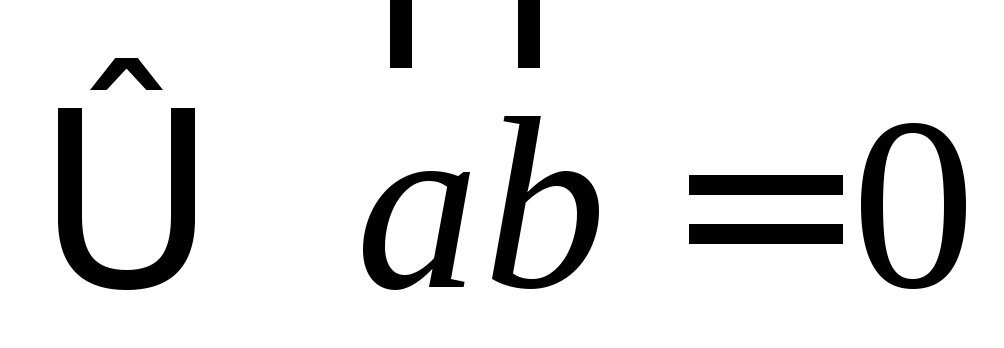Лекция 4 - 5. Векторное и смешанное умножение свободных векторов §10. Ориентация векторного пространства

Рассмотрим трехмерное векторное пространство , образованное всеми свободными векторами геометрического пространства.

Т е о р е м а. (условие компланарности трех векторов). Три вектора компланарны тогда и только тогда, когда определитель третьего порядка, составленный из координат этих векторов равен нулю.

Д о к а з а т е л ь с т в о. Векторы компланарны тогда и только тогда, когда система этих векторов является линейно зависимой, то есть существует нетривиальная линейная комбинация этих векторов, равная:, где. Записав это условие в координатах, получим систему трех линейных однородных уравнений

.

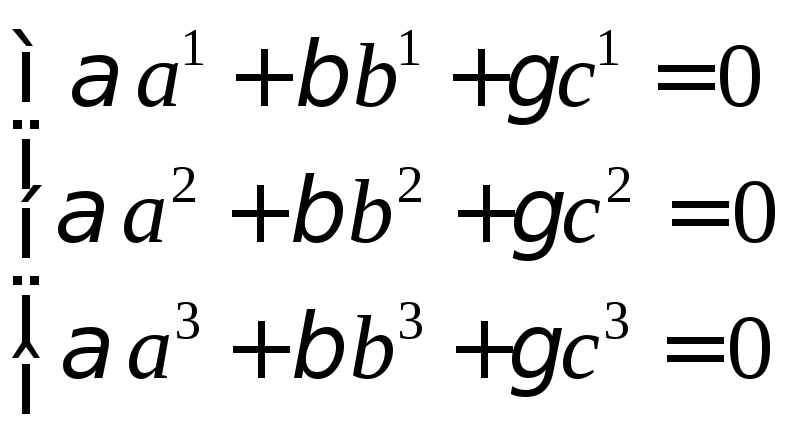Эта система имеет ненулевое решение , следовательно, её определитель равен нулю.

В пространстве существует бесконечное множество базисов. Пустьидва базиса. Векторы базисаможно выразить через векторы базиса:.

Матрица 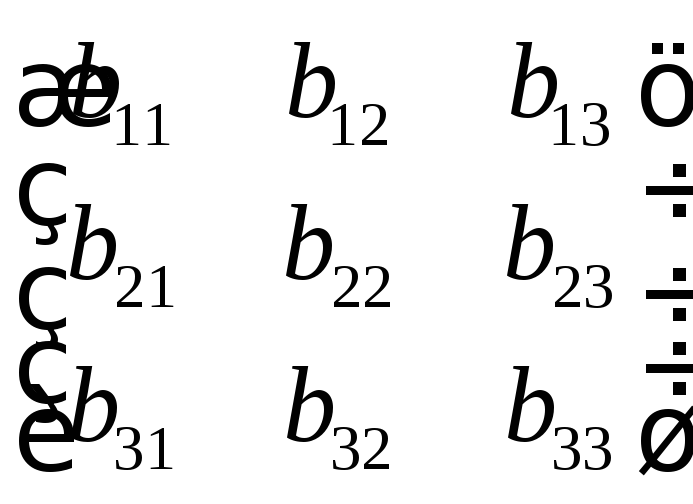, составленная из координат векторов, называетсяматрицей перехода от базиса к базису.

Обозначим определитель этой матрицы. Так как векторынекомпланарны, то.

Непосредственными вычислениями можно проверить, что:

1. ;

2. .

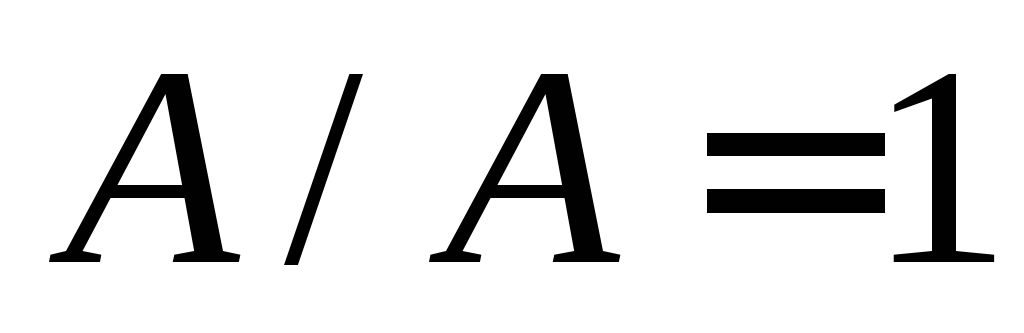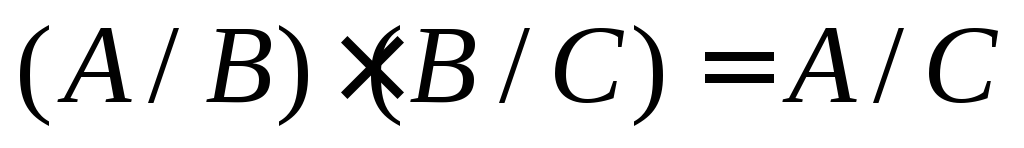Обозначим В множество всех базисов в пространстве . Будем говорить, что два базисаиориентированы одинаково , если. Очевидно, что:

1. ;

2. ;

3. .

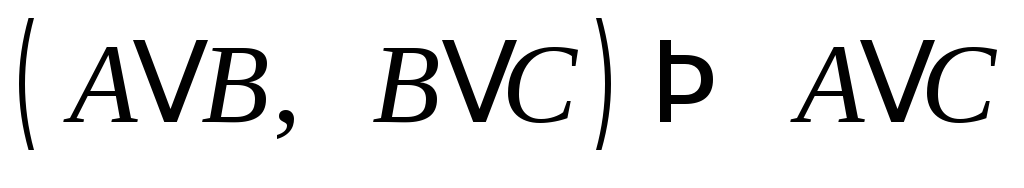Таким образом, отношение (быть одинаково ориентированными) на множествеВ всех базисов пространства является отношением эквивалентности. МножествоВ всех базисов разбивается на классы эквивалентности. Каждый класс состоит из всех одинаково ориентированных между собой базисов.

Т е о р е м а. Отношение разбивает множествоВ ровно на два класса эквивалентности.

Д о к а з а т е л ь с т в о. Рассмотрим два базиса: и. Тогда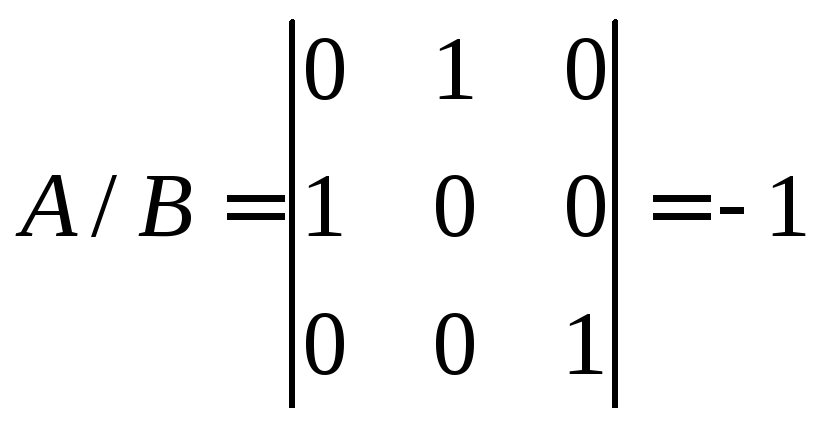. Следовательно, базисыине являются одинаково ориентированными, то есть принадлежат разным классам эквивалентностии. Для любого другого базисабудем иметь

.

То есть, либо , либои , следовательно, либо, либо. Таким образом получаем ровно два класса эквивалентности для отношения.

О п р е д е л е н и е. Каждый из классов эквивалентности отношения (быть одинаково ориентированными) называетсяориентацией пространства . Одна из них называетсяположительной или правой, другая отрицательной или левой.

Если тройка векторов принадлежит правой (левой) ориентации, то её называютправой (левой) тройкой векторов.

При циклической перестановке векторов ориентация тройки не меняется. Если два соседних вектора поменять местами, ориентация тройки меняется.

Внематематическое соглашение: правой будем считать тройку векторов , если со стороны векторавидно, что поворот отксовершается против часовой стрелки.