второго порядка. Если нет точек (x, y) с действительными координатами, удовлетворяющих уравнению (1) , то говорят, что уравнение (1) определяет мнимую кривую второго порядка. Уравнение x2 + y2 = −1 может служить примером уравнения второй степени, определяющего мнимую кривую, в данном случае мнимую окружность.
Важные случаи общего уравнения кривой второго порядка
Уравнение эллипса
x2 |
+ |
y2 |
= 1 (a ≥ b > 0) |
|
a2 |
b2 |
|||
|
|
с полуосями длины a и b . В частности, при a = b уравнение окружности
|
|
|
x2 |
+ y2 = a2 |
|
с центром в начале координат и радиусом a . |
|||||
Уравнение гиперболы |
|
|
|
|
|
|
x2 |
− |
y 2 |
|
=1 (a ≥ b > 0) |
|
a 2 |
b2 |
|
||
|
|
|
|
||
с полуосями a и b .
Уравнение параболы
y2 = 2 px (p > 0).
Уравнение пары пересекающихся прямых
a2 x2 −b2 y2 = 0 , (0 < a,b) или y = ± ba x .
Уравнение пары параллельных или совпадающих прямых x2 − a2 = 0 (a ≥ 0), или x = ±a .
y2 −b2 = 0, (b ≥ 0) или y = ±b .
Уравнение, определяющее точку |
|
|
|
x2 + y2 |
= 0 |
x = 0 |
. |
, или |
|||
|
|
y = 0 |
|
Эллипс
Эллипсом называется множество точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.
Теорема
Если известны: расстояние между фокусами F1 и F2 эллипса, равное 2c и сумма расстояний от любой точки на эллипсе до фокусов, равное 2a , то в прямоугольной декартовой системе координат, где ось Ox проходит через фокусы F1 и F2 (от F1 к F2 ), а начало координат посередине между ними, уравнение эллипса имеет вид
x2 |
+ |
y 2 |
=1, где b2 |
= a2 −c2 . |
|
a 2 |
b2 |
||||
|
|
|
30
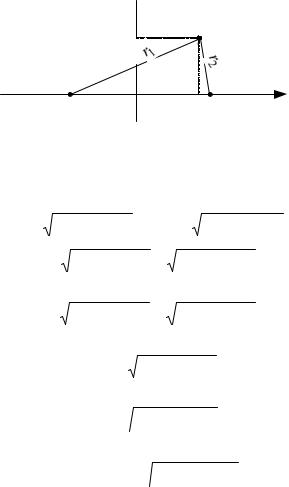
Доказательство
y
y |
M |
|
F1 |
F2 |
x |
−c |
x c |
Рис. 23.
Во введенной системе координат фокусы расположены на оси Ox и имеют координаты F1(− c, 0) и F2 (c, 0). Пусть точка M (x, y) принадлежит эллипсу (рис.23). Тогда
MF = |
(x + c)2 + y2 , MF = (x −c)2 |
+ y2 |
, |
1 |
2 |
|
|
2a = (x + c)2 + y2 + (x −c)2 + y2 ,
перенося первый радикал из правой части в левую, запишем
2a − (x + c)2 + y2 = (x −c)2 + y2 .
Возведем обе части уравнения в квадрат
4a2 + (x + c)2 + y2 − 4a (x + c)2 + y2 = (x −c)2 + y2
и раскроем квадраты в левой и правой частях
4a2 + x2 + 2cx + y2 + c2 − 4a
(x + c)2 + y2 = x2 − 2xc + c2 + y2 .
Приводя подобные члены, получим уравнение
4a2 + 4cx = 4a
(x + c)2 + y2 ,
обе части которого разделим на 4 и снова возведем в квадрат. тогда уравнение примет вид
a4 + 2a2cx + c2 x2 = a2 [x2 + 2cx + c2 + y2 ].
Последнее уравнение можно упростить, если раскрыть скобки и привести подобные члены,
a4 + 2a2cx + c2x2 = a2x2 + 2a2cx + a2c2 + a2 y2 , − (a2 −c2 )x2 = −a2(a2 −c2 )+ a2 y2 .
Поскольку из определения эллипса следует, что 2a > 2c , то число a2 −c2 > 0 и его можно обозначить, как b2 = a2 −c2 . Тогда уравнение эллипса запишется в виде
−b2 x2 = −a2b2 + a2 y2 , или a2b2 = b2 x2 + a2 y2 .
Разделив последнее уравнение на a2b2 , получим
x2 |
+ |
y 2 |
=1. |
|
a 2 |
b2 |
|||
|
|
Такое уравнение эллипса называется каноническим.
31
Исследование формы кривой
Если в уравнении эллипса |
x2 |
+ |
y 2 |
=1 заменить x на − x , то его вид не изменится. |
|
a 2 |
b2 |
||||
|
|
|
Это означает, что если точка M (x, y) принадлежит кривой, то точка M1(− x, y) также
принадлежит этой кривой. Следовательно, кривая симметрична относительно оси ординат. Эллипс симметричен и относительно оси абсцисс, потому что его уравнение не меняется при замене y на − y . Учитывая это, достаточно изучить вид кривой в первой четверти,
то есть при условии x, y ≥ 0. |
|
|
|
|
|
|
||||
При |
x, y ≥ 0 |
можно задать кривую |
в виде |
явного уравнения |
y = b |
a2 − x2 , |
||||
|
|
|
|
|
|
|
|
|
a |
|
(0 ≤ x ≤ a). Из этого уравнения ясно, что кривая проходит через точки B(0,b) |
и A(a,0). |
|||||||||
Эти точки называются вершинами эллипса. |
|
|
|
|
||||||
Эллипс |
|
— |
ограниченная кривая, |
которая |
находится внутри |
прямоугольника |
||||
0 ≤ x ≤ a |
. |
Из |
явного уравнения |
эллипса ясно, |
что ордината y при |
непрерывном |
||||
|
|
|||||||||
0 ≤ y ≤ b |
|
|
на отрезке [0, a] |
|
|
|
|
|
|
|
возрастании |
x |
монотонно убывает. Следовательно, |
эллипс есть |
|||||||
непрерывная замкнутая кривая, в первой четверти она выпукла вверх, в любой ее точке можно провести касательную. В остальных четвертях кривая строится с учетом симметрии относительно координатных осей.
Числа a и b называются полуосями эллипса. Поскольку b2 |
= a2 −c2 , то a > b |
и |
||||||
эллипс вытянут вдоль оси Ox . При этом a |
называется большей полуосью, а b |
- |
||||||
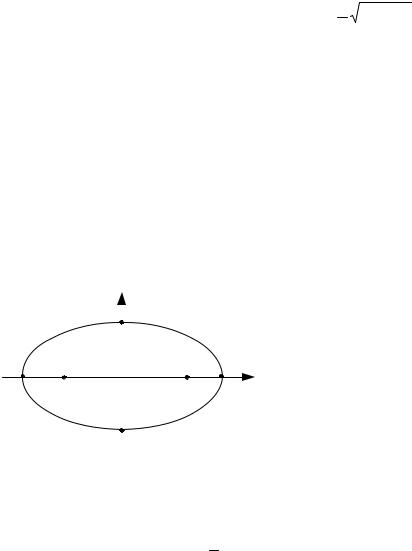
меньшей полуосью эллипса. Вид кривой показан на рисунке 24. |
|
|
|
|||||
|
y |
|
|
|
|
|
||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F1 |
|
|
F2 |
|
x |
|
|
−a |
−c |
|
|
c |
a |
|
|
|
|
|
|
|
|
||||
|
−b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рис. 24. |
|
|
|
|
|
||
При a = b эллипс представляет собой окружность радиуса |
a с центром в начале |
|||||||
координат. Уравнение этой окружности |
|
|
|
|
|
|||
x2 + y2 = a2 .
Эксцентриситетом эллипса называется число ε = ac . Для эксцентриситета эллипса
справедливо неравенство 0 < ε <1, поскольку из определения эллипса следует, что c > a > 0. Эксцентриситет окружности ε = 0 , поскольку для окружности a = b и c = 0 .
Учитывая то, что эксцентриситет окружности ε = 0 , можно сделать вывод, что чем больше эксцентриситет эллипса, тем больше он вытянут относительно одной из осей симметрии.
Гипербола
Гиперболой называется множество точек, разность расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.
32
Теорема |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Если известны: расстояние |
между фокусами F1 и |
F2 гиперболы, равное |
2c и |
||||||||||||||||||||||
разность расстояний от любой ее точки до фокусов, равное |
2a , то в прямоугольной |
||||||||||||||||||||||||||
декартовой системе координат, где ось Ox проходит через фокусы F1 и F2 (от F1 |
к F2 ), |
||||||||||||||||||||||||||
а начало |
координат посередине |
между фокусами, уравнение гиперболы имеет вид |
|||||||||||||||||||||||||
|
x2 |
− |
y2 |
|
= |
1, где |
a,b > 0 и b |
2 |
= c |
2 |
− a |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Доказательство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
A |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−c |
|
|
|
|
|
|
|
x c |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 25. |
|
F1(−c,0), F2(c,0). |
|
||||||||
|
|
Во введенной системе |
xOy |
координаты фокусов равны |
Если |
||||||||||||||||||||||
точка A(x, y) |
принадлежит |
|
гиперболе, |
то справедливо |
|
AF1 − AF2 |
|
= 2a , |
или |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
AF1 − AF2 |
= ±2a (рис.25). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Подставив в последнее равенство координаты точек A, F1, F2 , получим |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
(x + c)2 + y2 − (x −c)2 + y2 = ±2a , |
|
|||||||||||||||||||
|
|
|
|
|
|
|
или |
(x + c)2 + y2 = |
(x −c)2 + y2 |
± 2a . |
|
||||||||||||||||
|
|
Возведем обе части последнего уравнения в квадрат |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
(x + c)2 + y2 = (x −c)2 + y2 ± 4a (x −c)2 + y2 + 4a2 |
|
|||||||||||||||||||
и упростим его, раскрыв все квадраты
x2 + 2cx + c2 + y2 = x2 − 2cx + c2 + y2 ± 4a
(x −c)2 + y2 + 4a2
и приведя подобные члены
4cx − 4a2 = ±4a
(x −c)2 + y2 .
Последнее уравнение разделим на 4 и снова возведем в квадрат c2 x2 − 2cxa2 + a4 = a2 (x2 − 2cx + c2 + y2 ).
Раскрыв скобки и сделав упрощения, получим уравнение
(c2 − a2 )x2 − a2 y2 = a2(c2 − a2 ),
в котором c2 − a2 > 0, поскольку 2c > 2a из определения гиперболы. Из этого следует, что можно ввести обозначение и записать уравнение гиперболы в виде b2 x2 − a2 y2 = a2b2 . Разделив на a2b2 , получим уравнение гиперболы
ax22 − by22 =1,
которое называется каноническим.
33