Геометрия

Часть I

1. ВЕКТОРЫ. Сложение векторов и умножение вектора на число. Коллинеарность и компланарность. Координаты вектора в аффинной системе координат. Скалярное и векторное произведения. Свойства, геометрический смысл этих произведений и их выражение в координатах.

Вектором называется направленный отрезок АВ с начальной точкой А и конечной точкой В, который обозначается символом или одной строчной буквой (рис. 3.1).

Длиной (или модулем) вектора называется число, равное длине отрезка, изображающего вектор. Записи и обозначают модули векторов и соответственно. Вектор , длина которого равна единице, называется единичным вектором, или ортом: орт обозначается .

Вектор, у которого начало и конец совпадают, называется нулевым и обозначается символом . Длина такого вектора равна нулю и ему можно приписать любое направление.

Векторы и , расположенные на одной прямой или на параллельных прямых, называются коллинеарными ( ).

Два вектора называются равными (), если они: 1) имеют равные модули; 2) коллинеарны; 3) направлены в одну сторону.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства. В этом случае вектор называется свободным.

Векторы называются компланарными, если они лежат на одной или на параллельных плоскостях.

Рассмотрим линейные операциями над векторами.

Произведением вектора на действительное число называется вектор , длина которого , а направление совпадает с , если , и противоположно , если . Из определения следует, что векторы и всегда расположены на одной или на параллельных прямых. Следовательно, равенство

(2.1)

выражает условие коллинеарности двух векторов.

Противоположным вектором называется произведение вектора на число , т.е. . Если , то орт вектора находится по формуле

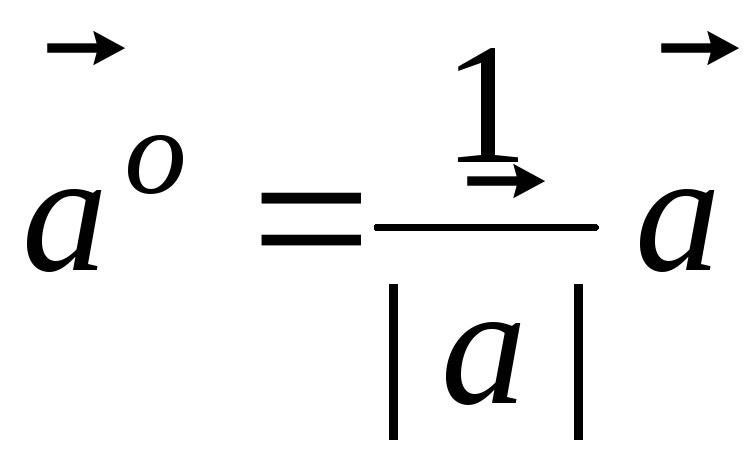. (2.2)

Суммой двух векторов и называется вектор , который идет из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (рис. 3.2, а) (правило треугольника). Очевидно, что вектор в этом случае представляет диагональ параллелограмма, построенного на векторах и (рис. 3.2, б) (правило параллелограмма).

Аналогично определяется сумма нескольких векторов: если векторы , ,…, образуют ломаную , то суммой этих векторов является вектор , замыкающий эту ломаную (рис. 3.2, в) (правило многоугольника).

В частности, если ломаная замыкается, т.е. , то сумма ее звеньев равна нулевому вектору .

Р азностью двух векторов и называется вектор , являющийся суммой векторов и . Отметим, что вектор направлен к концу вектора , если и приведены к общему началу ( рис. 2.2, б).

Введенные операции умножения вектора на число и сложения векторов называются линейными и удовлетворяют ( и ) следующим свойствам:

1о. ; 2о. ; 3о. ;

4о. ; 5о. ; 6о. 1 = ;

7о. ; 8о. () = +.

Скалярное и векторное произведения. Свойства, геометрический смысл этих произведений и их выражение в координатах.

С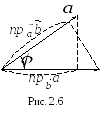калярным произведением двух векторов и (обозначается ) называется число, равное произведение модулей перемножаемых векторов на косинус угла между ними (рис. 3.6). Таким образом, по определению

. (2.16)

Так как произведение есть проекция вектора на ось, определяемую вектором (обозначается ), и - проекция вектора на ось вектора (обозначается ), то из (3.16) следует, что

. (2.17)

Скалярное произведение двух векторов равно модулю одного из векторов, умноженному на проекцию на него другого вектора. Из (3.17) находим выражения для проекции одного вектора на направление другого:

(2.18)

В частном случае, если , то

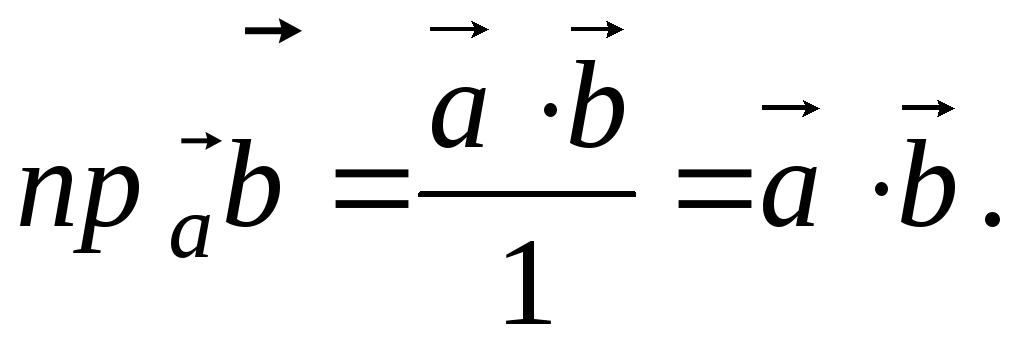(2.19)

Проекция вектора на единичный вектор равна скалярному произведению этих векторов.

Рассмотрим некоторые свойства скалярного произведения.

1о. Скалярное произведение коммутативно:

.

2о. Скалярное произведение ассоциативно относительно скалярных множителей:

3о. Скалярное произведение дистрибутивно относительно суммы векторов:

.

4о. (либо , либо , либо ). Таким образом, условием ортогональности (перпендикулярности) двух ненулевых векторов и является равенство нулю их скалярного произведения, т.е.

Рассмотрим теперь скалярное произведение вектора самого на себя. Такое произведение называется скалярным квадратом вектора:

.

Таким образом,

, (2.20)

т.е. скалярный квадрат вектора равен квадрату его модуля.

Найдем выражение скалярного произведения через проекции перемножаемых векторов. Координатные орты имеют длины, равные единице, т.е. . Далее, так как эти векторы взаимно ортогональны, то .

Пусть даны два вектора и . В таком случае

, (2.21)

т.е. скалярное произведение двух векторов равно сумме парных произведений их одноименных координат.

В частности, положив в (2.21) , найдем

.

Отсюда следует, что

. (2.22)

Используя координатную форму скалярного произведения, получаем, что условие ортогональности ненулевых векторов и имеет вид

. (2.23)

Выражая скалярное произведение и модули векторов через их проекции по формулам (3.21) и (3.22), получим формулу для нахождения косинуса угла между векторами:

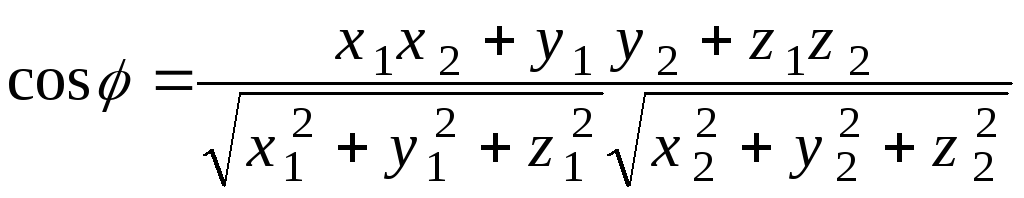. (2.24)

Пусть дан вектор и ось l, которая составляет с базисными векторами соответственно углы . Найдем . Для этого зададим направление оси l ортом . Тогда, согласно (2.19)

. (2.25)

Будем предполагать, что в пространстве R3 выбрана правая система декартовых прямоугольных координат {0, i, j, k}.

Векторным произведением вектора а на вектор b называется вектор c, который определяется следующими тремя условиями:

1. Длина вектора c численно равна площади параллелограмма, построенного на векторах a и b, т. е. c  = a  b sin (a^b).

2. Вектор c перпендикулярен к каждому из векторов a и b.

3. Векторы a, b и c, взятые в указанном порядке, образуют правую тройку.

Для векторного произведения c вводится обозначение c = [ab] или c = a b.

Если векторы a и b коллинеарны, то sin(a^b) = 0 и [ab] = 0, в частности, [aa] = 0. Векторные произведения ортов: [ij] = k, [jk] = i, [ki] = j.

Если векторы a и b заданы в базисе i, j, k координатами a(a1, a2, a3), b(b1, b2, b3), то

[ab] = 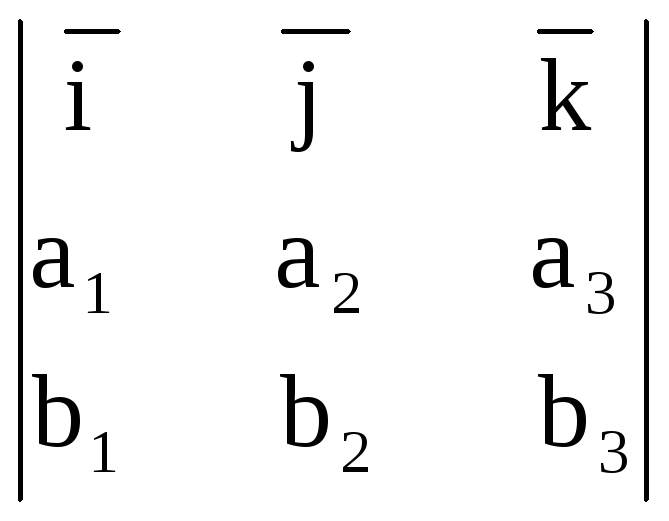=i (a2b3 - a3b2) - j (a1b3 - a3b1) + k (a1b2 - a2b1).

Если векторное произведение двух векторов а и b скалярно умножается на третий вектор c, то такое произведение трех векторов называется смешанным произведением и обозначается символом a b c.

Если векторы a, b и c в базисе i, j, k заданы своими координатами a(a1, a2, a3), b(b1, b2, b3), c(c1, c2, c3), то

abc = .

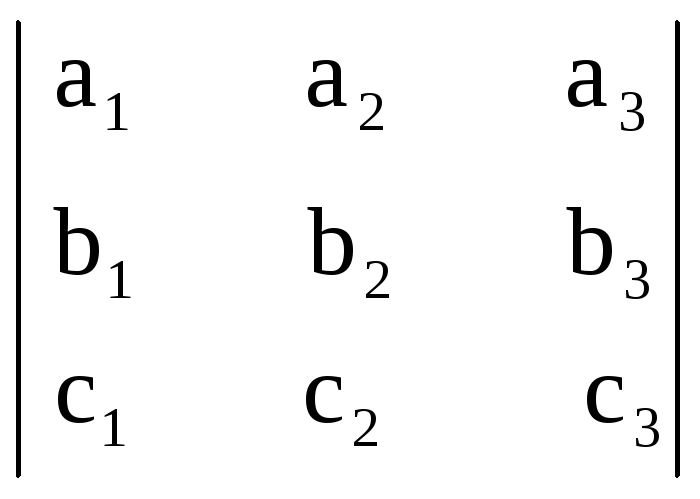Смешанное произведение имеет простое геометрическое толкование - это скаляр, по абсолютной величине равный объему параллелепипеда, построенного на трех данных векторах.

Если векторы образуют правую тройку, то их смешанное произведение есть число положительное, равное указанному объему; если же тройка a, b, c - левая, то a b c<0 и V = - a b c, следовательно V = a b c .

Координаты векторов, встречающиеся в задачах первой главы, предполагаются заданными относительно правого ортонормированного базиса. Единичный вектор, сонаправленный вектору а, обозначается символом а^о. Символом r=ОМ обозначается радиус-вектор точки М, символами а, АВ или а , АВ  обозначаются модули векторов а и АВ.

2. ПРЯМАЯ И ПЛОСКОСТЬ. Теорема о параметрическом уравнении прямой в пространстве. Теорема об общем уравнении плоскости в пространстве. Нормальный вектор и теорема о расстоянии от точки до плоскости.

В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y)=0. При этом на функцию F должны быть наложены ограничения так, чтобы, с одной стороны, это уравнение имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло “куска плоскости”. Важный класс линий составляют те, для которых функция F(x,y) есть многочлен от двух переменных, в этом случае линия, определяемая уравнением F(x,y)=0, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени, cуть прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.

Пусть прямая в аффинной системе координат Oxy определяется уравнением

Ax + By +C = 0. (1)

Теорема. Точки М₁(x₁, y₁) и М₂(x₂, y₂) принадлежат разным полуплоскостям относительно прямой l тогда и только тогда, когда

(Ax₁ + By ₁+C)(Ax₂ + By ₂+C) < 0. (2)

Доказательство. Предварительно заметим, что точка М₀(x₀, y₀) являетяс внутренней точкой отрезка [М₁М₂] тогда и только тогда, когда , где 0 < t < 1, т.е. x₀ = x₁ + tx₂, y₀ = y₁ + ty₂, 0 < t <1. Точки М₁(x₁, y₁) и М₂(x₂, y₂) принадлежат разным полуплоскостям тогда и только тогда, когда существует точка М₀(x₀, y₀), общая для прямой l и отрезка [М₁М₂], причем точка М₀ является внутренней точкой отрезка [М₁М₂], т.е.

С учетом очевидного тождества С = tC + (1 - t)C получим, что точки М₁, М₂ принадлежат разным полуплоскостям тогда и только тогда, когда существует число t такое, что t(Ax₁ + By ₁+C) + (1 - t)(Ax₂ + By ₂+C) = 0, 0 < t <1, или в обозначениях Ax₁ + By ₁+C = F₁, Ax₂ + By ₂+C = F₂, (1 -t)F₁ + tF₂, 0 < t < 1. Это равносильно тому. что F₁F₂ < 0. Теорема доказана.

Итак, для координат (x, y) всех одной полуплоскости выполняется неравенство Ax + By +C > 0, а другой − неравенство Ax + By +C < 0. Полуплоскость, для точек М(x, y) которой Ax + By +C > 0, называется положительной полуплоскостью относительно уравнения (6.1.1) прямой l и обозначается символом π₊, а полуплоскость, для точек которой Ax + By +C < 0, − отрицательной полуплоскостью и обозначается π_-.

Теорема об общем уравнении плоскости в пространстве

Пусть плоскость π в аффинной системе координат Oxyz определяется уравнением

Ax + By +Cz + D = 0. (1)

Теорема 6.4. Точки М₁(x₁, y₁, z₁) и М₂(x₂, y₂, z₂) принадлежат разным полупространствам относительно плоскости π тогда и только тогда, когда

(Ax₁ + By₁+Cz₁ + D)(Ax₂ + By ₂+Cz₂ + D) < 0. (1)

Доказательство теоремы аналогично доказательству предыдущей теоремы

Полупространство, для точек М(x, y, z) которого Ax + By +Cz + D > 0, называется положительнsv полупространством относительно уравнения (1) плоскости π, а полупространство, для точек которого Ax + By +Cz + D < 0, − отрицательным полупространством.

Расстояние от точки до плоскости.

Теорема 6.6. В прямоугольной декартовой системе координат Oxyz расстояние от точки М₀(x₀, y₀, z₀) до плоскости) определяется формулой

(1)

Угол между плоскостями. Пусть плоскости π₁ и π₂ заданы уравнением

π_i : Ax_i + By_i+Czsub>i + D = 0, A_i² + B_i² + C_i² ≠ 0, i = 1, 2, (2)

Вообще говоря, две пересекающиеся плоскости π₁ и π₂ образуют два угла, в сумме равные π. Достаточно определить один из них. Так как векторы нормали n₁ и n₂ перпендикулярны плоскостям, то угол φ = совпадают с одним из углов между плоскостями π₁ и π₂. угол φ между плоскостями (2), совпадающий с углом между их нормалями, определяются формулой

. В частности, плоскости π₁ и π₂ перпендикулярны тогда и только тогда, когда A₁A₂ + В₁В₂ + С₁С₂ = 0.