
EKZAMEN - копия
.PDF
Обозначим через  единичный нормальный вектор к поверхности S в точке (x,y,z). Если поверхностьS гладкая и векторная
единичный нормальный вектор к поверхности S в точке (x,y,z). Если поверхностьS гладкая и векторная
функция  непрерывна, то в каждой точке поверхности существуют два противоположно направленных единичных нормальных вектора:
непрерывна, то в каждой точке поверхности существуют два противоположно направленных единичных нормальных вектора:
Выбор одного из них называется ориентацией поверхности.
Если S является границей ограниченной области, то ее можно ориентировать внешней или внутреннейнормалями. Поверхность S, ориентированную внешней нормалью, называют ее внешней стороной, а ориентированную внутренней нормалью, − ее внутренней стороной.
Поверхностный интеграл второго рода от векторного поля  по
по
ориентированной поверхности S (илипоток векторного поля  через поверхность S) может быть записан в одной из следующих форм:
через поверхность S) может быть записан в одной из следующих форм:
Если поверхность S ориентирована внешней нормалью, то
Если поверхность S ориентирована внутренней нормалью (k-компонент вектора нормали является отрицательным), то
Поверхностный интеграл второго рода можно записать также в
координатной форме. Пусть P (x,y,z), Q (x,y,z),R (x,y,z) являются
компонентами векторного поля  . Введем cos α, cos β, cos γ − направляющие косинусы внешней нормали
. Введем cos α, cos β, cos γ − направляющие косинусы внешней нормали  к поверхности S. Тогда
к поверхности S. Тогда
скалярное произведение  равно
равно
Следовательно, поверхностный интеграл можно записать в виде
Если поверхность S ориентирована внутренней нормалью, то
Поскольку |
(рисунок 1), и, |
аналогично,  , получаем следующую формулу для вычисления поверхностного интеграла II рода:
, получаем следующую формулу для вычисления поверхностного интеграла II рода:
Величина  называется векторным элементом поверхности. Точка обозначает скалярное произведение соответствующих векторов. Частные производные, входящие в последние формулы, вычисляются следующим образом:
называется векторным элементом поверхности. Точка обозначает скалярное произведение соответствующих векторов. Частные производные, входящие в последние формулы, вычисляются следующим образом:
Если поверхность S задана явно в виде уравнения z = z(x,y), где z(x,y) − дифференцируемая функция в областиD(x,y), то
поверхностный интеграл второго рода от векторного поля  по поверхности S записывается в одной из следующих форм:
по поверхности S записывается в одной из следующих форм:
Если поверхность S ориентирована внешней нормалью (k- компонент вектора нормали является положительным), то
Если поверхность S задана в параметрической форме с помощью
вектора  , то последняя формула принимает вид
, то последняя формула принимает вид
где (u,v) изменяются в пределах области интегрирования D(u,v).

Рис.1
Если поверхность S не представима в явном или параметрическом виде, то ее можно попробовать разбить на конечное число частей, каждая из которых представима в таком виде. В этом случае справедливо свойство аддитивности: поверхностный интеграл второго рода по поверхности S будет равен сумме интегралов по ее частям.
11. Формула Стокса.
Пусть S является гладкой поверхностью, ограниченной гладкой кривой C. Тогда для любой непрерывно дифференцируемой векторной функции
справедлива теорема Стокса:
второго рода с соответствующими тройными интегралами. Данную формулу можно записать также в координатной форме:
В частном случае, полагая |
, получаем формулу |
для вычисления объема тела G: |
|
где
− ротор векторного поля |
. |
Символ  показывает, что криволинейный интеграл вычисляется по замкнутой кривой.
показывает, что криволинейный интеграл вычисляется по замкнутой кривой.
Будем предполагать, что ориентация поверхности и направление обхода кривой соответствуют правилу правой руки. В этом случае при обходе кривой поверхность всегда остается слева, если голова
направлена в ту же сторону, что и вектор нормали  (рисунок 1). Теорема Стокса связывает между собой криволинейные интегралы второго рода и поверхностные интегралы второго рода.
(рисунок 1). Теорема Стокса связывает между собой криволинейные интегралы второго рода и поверхностные интегралы второго рода.
В координатной форме теорема Стокса может быть записана в следующем виде:
В.Элементы векторного анализа 1.Основные характеристики скалярного и векторного полей.
Рис.1 Рис
12. Формула Остроградского-Гаусса.
Обозначим |
через G трехмерное тело, ограниченное |
кусочно- |
|||
непрерывной, |
гладкой, замкнутой |
поверхностьюS с |
внешней |
||
нормалью. |
Предположим, |
что |
задано |
векторное |
поле |
компоненты которого имеют непрерывные частные производные. Согласно формуле Остроградского-Гаусса,
|
|
где через |
|
|
|
обозначена дивергенция векторного поля |
(она обозначается также |
||||
символом |
). Символ |
|
указывает, |
что |
поверхностный |
интеграл |
вычисляется |
по |
замкнутой |
поверхности. |
|
Формула Остроградского-Гаусса связывает поверхностные интегралы

2. |
Градиент, |
ротор, |
дивергенция. |

3. Потенциальные поля. |
Условия потенциальности |
векторного |
поля. |
4. Соленоидальное и гармоническое поле.

Если дивергенция и ротор векторного поля  определены в каждой точке конечной открытой области V пространства, то всюду в V функция может быть представлена в виде суммы безвихревого поля
определены в каждой точке конечной открытой области V пространства, то всюду в V функция может быть представлена в виде суммы безвихревого поля 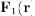 и соленоидального поля
и соленоидального поля  :
:
где
для всех точек  области V.
области V.
Г. Ряд и интеграл Фурье
1. Ортогональная система функций . Ряд Фурье.
система функций {(φn (x)}, n = 1, 2,..., ортогональных с весом ρ (х) на отрезке [а, b], т. е. таких,
что
2. Свойства ряда Фурье. Неравенство Бесселя. Сходимость в среднем.
5. Теорема Гельмгольца
Или


3. Тригонометрический ряд Фурье и его свойства.
Тригонометрический ряд Фурье — представление произвольной функции  с периодом
с периодом  в виде ряда
в виде ряда
(1)
или используя комплексную запись, в виде ряда:
 .
.
Все утверждения этого параграфа верны в предположении, что участвующие в них функции (и результаты операций с ними)
лежат в пространстве  .
.
Вычисление коэффициентов Фурье является линейной операцией:
Справедливо равенство Парсеваля:
 .
.
Коэффициенты Фурье производной легко выражаются через коэффициенты Фурье самой функции:
коэффициенты Фурье произведения двух функций выражаются сверткой коэффициентов Фурье сомножителей:

рассмотрим операцию свертки функций:
где функции предполагаются периодически продолженными с промежутка  на всю прямую. Тогда
на всю прямую. Тогда
4. Теорема Дирихле. шпора
5.Принцип локализации Римана.
6.Метод средних арифметических суммирования ряда Фурье. Теорема Вейерштрасса.
7. Преобразование Фурье. 8. Интеграл Фурье.


