Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный аграрный университет Северного Зауралья

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика 3 семестр

.pdf

Скачиваний:

Добавлен:

14.04.2015

Размер:

2.31 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 114 5 6 7 8 9 10 11 > Следующая >>>

Геометрически dy представляет собой приращение ординаты касательной к графику функции в заданной точке.

dx x - дифференциал аргумента равен приращению аргумента.

y - дифференциал функции и приращение функции равны лишь приближённо.

f x x f x f x x - формула для приближённых вычислений.

Таблица дифференциалов и производных основных элементарных функций.

Элементарные функции

1.Степенная функция y xn

2.Линейная функция

y ax b	a,b-постоянные

y=x.

3.Тригонометрич. функции y=sin x

y=cos x y=tg x y=ctg x

4. Показательная функция

y a
x
	, a-число

y ex , e 2,718

5. Логарифмическая функция

y log	a	x
	a
y=ln x

6. Иррациональная функция

y	n	x, n число

df x

f x dx

дифференциал

n 1

d ax b a dx

d x dx

d sin x cos xdx

d cos x sin xdx

dtgx

cos

dctgx

sin

ln adx

d log

x ln a

d ln x

n 1

производная

n 1

ax b

cos x

sin x

cos x

tgx

cos

ctgx

sin

ln a

e x

log

x ln a

ln x

n 1

7. Обратно тригонометрические функции

y= arcsin x

y=arcos x

y= arctg x

d arcsin x			dx
d arcsin x		1		x
		1		x
				2
d arccosx					dx


				1 x2
				1 x2
d arctgx		dx

	1 x 2

		1
arcsin x		1


		x2
	1	x2
			1
arccosx			1


		1	x2
		1	x2
	1
arctgx	1

	1 x 2

y=arcctg x

8. y=c c-const

	dx					1
d arcctgx	dx		arcctgx			1
d arcctgx	x	2	arcctgx			x	2
1	x				1	x

d(c)=0·dx
d(c)=0·dx			с	0
			с	0

дифференцирования

Основные

правила

Пусть С - постоянное, U U x
								и
Тогда :
		0
1)	с	0
1)
		1
2)	x	1
2)
				U V
3)	U V			U V
3)
			CU
4)	CU		CU
4)
			U V UV
5)	UV		U V UV
5)
	U
	U
6)						2
6)	V			V


7) если		y		f U	,	U U x	, т.е	y	f
7) если					,		, т.е

- функции имеющие производные.

где функции f (U) и

U (x) имеют производные, то

функции.

y	y	U
x	u	x

- правило дифференцирования сложной

4.2Определение функции 2-х аргументов

Определение. Если каждой паре действительных чисел (x,y) D по некоторому правилу (закону) поставлено в соответствие одно и только одно значение переменной Z E, то говорят, что на множестве D задана функция z =f(x,y).

Множество D-область определения функции.

Область D есть часть плоскости, ограниченная замкнутой линией. Графиком функции z =f(x,y) является некоторая поверхность Q.

0		y

x D(z)

Пример. Найти область определения функции

z	a	2	x	2	y	2
		2		2		2

Решение:

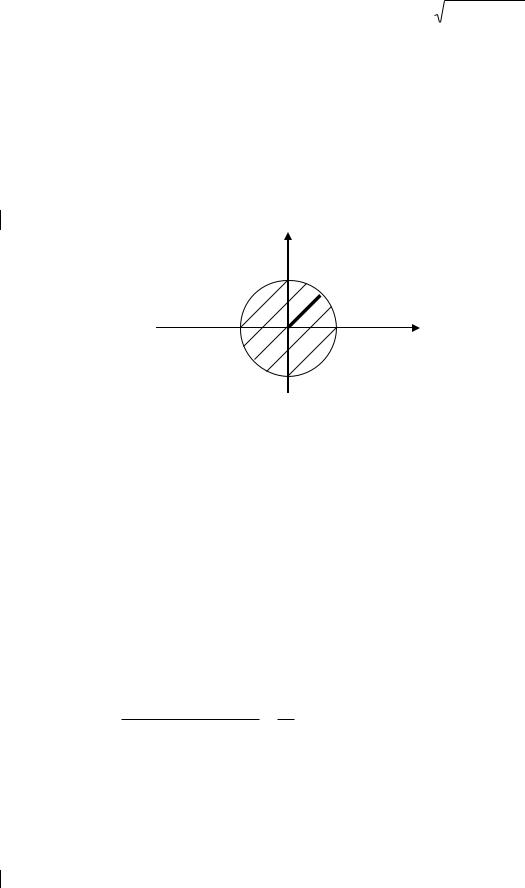
Функция z принимает действительные значения при условии a2-x2-y2≥0→x2+y2≤ a2 круг с центром в начале координат, радиус круга a.

Ответ: Областью определения данной функции является круг вида x2+y2 ≤ a2 (граница-окружность включается)

Изображение области определения на координатной плоскости ХОУ.

4.3 Производные и дифференциалы функции 2-х аргументов

Основные формулы

lim

f x x, y f x, y

f x, y z

x 0

x - частная производная 1-го порядка

функции z

по переменной x.

lim

f x, y y f x, y

f x, y z

y 0

- частная производная 1-го порядка

функции Z

по переменной y.

вычисляется при постоянном y, y

вычисляется при постоянном x.

При вычислении x ,

y используются правила и формулы дифференцирования

(смотреть таблицу производных).
3.dz f x x, y dx f y x, y dy	полный дифференциал функции
3.dz f x x, y dx f y x, y dy	z f x, y

	f	x, y dx d		x	z
		x
где			x, y dy d y z			- частные

	f y

1. Для дифференцируемой функции равенства.

	z	f x, y
			дифференциал функции
z	f x, y		справедливы приближённые
z	f x, y

а)

z dz

, где

- полное приращение функции.

z f x x, y y f x, y

dzполный дифференциал.

x, y z

Эта функция используется в нахождении

приближённых значений функции.

x, y z

5.Частными производными второго порядка от

x y

функции z f x; y

называются

x, y z

частные производные от её частных производных

первого

порядка.

x, y z

y x

- Обозначения частных

производных 2-го порядка от

функции z = f(x,y), причём

x y

y x

dxdy

x y

дифференциал второго порядка для функции

z f x, y

Если z = f(x,y)

где x = φ(t) , y=ψ(t) , то

- производная

сложной

функции .z=f(φ(t),ψ(t)).

x ,

Если z=f (x,y),

где

y ,

то

9. Производная неявной функции, заданной уравнением, где дифференцируемая

функция,	F(x, y) 0
	F(x, y) 0
			F
		y	x	F x
вычисляется	по формуле:	y	F	F
вычисляется	по формуле:		F	F
				y
			y

10.	Частные производные неявной функции заданной уравнением вычисляются по
формулам:			F(x, y, z) 0
			F(x, y, z) 0
		F
z		x	F
		x	x
x		F	F
x		F	F
			z
		z
			F

z	y	F
		y
y	F	F z

	z

при условии

Fz 0

4.4Примеры решения задач

а)

б)

в)

г)

Задача 1.			Найти производные

y ln 4	4x 1
y ln 4	4x 1
	4x 1
		arctgx
y x 1
cos xy		x	0
cos xy		y	0
		y
x a cost at b sin t

y a sin t at b cost

Решение:

или

dy dx

следующих функций:

а) Пользуясь правилом логарифмирования корня и дроби, преобразуем правую часть:

y 14 ln 4x 1 ln 4x 1 .

Применяя правила и формулы дифференцирования, получим:

y	1	4	4	1	1	2
				4x 1	4x 1	16x	2	1

	4 4x 1		4x 1

б) Предварительно прологарифмируем по основанию е обе части равенства: ln y arctgxln x 1

Теперь дифференцируем обе части, считая

ln y

сложной функцией от

переменной х:

1	y	1		ln x 1 arctgx	1	ln x 1		arctgx	,
y		1 x	2		x 1	1 x	2	x 1

откуда

y x 1	arctgx	ln x 1			arctgx
			1 x	2	x 1

в) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную у', следует дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной у'. Имеем

Из полученного равенства, находим производную у':

		sin xy y xy					y xy		0.
		sin xy y xy					y	2	0.
								2

связывающего х, у, и у',
y	3	sin xy xy	2		y sin xy y xy 0,
y		sin xy xy			y sin xy y xy 0,
		y x xy		2		sin xy y y				3	sin xy ,
		y x xy				sin xy y y					sin xy ,

откуда

	y y	3		sin xy	y 1 y
y
	x xy		2	sin xy	x 1 y

2 2

	sin xy	.
	sin xy	.
	sin xy

г) Зависимость между переменными х и у задана параметрическими уравнениями.

Чтобы найти искомую производную у', находим предварительно дифференциалы dy и dx и затем берем отношение этих дифференциалов

dx a sin t a sin t at b cost dt at b costdt;

dy a cost a cost at b sin t dt at b sin tdt;

at b sin tdt

tgt.

at b costdt

Задача 2. Найти производную второго порядка y

а)

4 y 3 x 2 2x 5 0;

б)

x 2cos3 t; y 6sin3 t.

Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе

части заданного уравнения, считая при этом у функцией от х:

4 y

2x 2

4 y 3

(1)

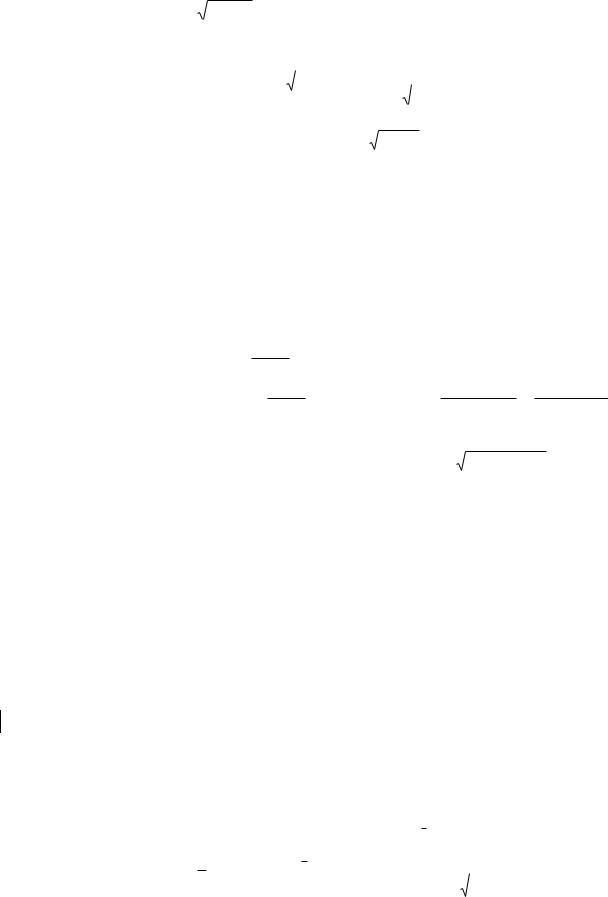
откуда

y x 1

4 y 3.

Снова дифференцируем по х обе части (1):

		4 y
y	4 y 3 x 1	4 y	(2)


		4 y 3
	2	4 y 3

Заменив у' в (2) правой частью (1), получим:

y	4 y 3 2 x 1	.
	2

б) Зависимость между переменными x и у задана параметрическими уравнениями. Чтобы найти производную у', находим сперва дифференциалы dy и dx и затем берем отношение этих дифференциалов:

dy 18sin	2	t costdt;

dx 6cos	2	t sintdt.

Тогда

18sin2 t costdt

3tgt.

6 cos2 t sin tdt

Производная второго порядка y

. Следовательно, чтобы найти у", надо найти

дифференциал dy':

3dt

cos

3dt

( 6 cos

t sin tdt)

cos

2 cos

t sin t

sin 2t cos

Тогда

Задача 3. Найти приближенное значение функции

4x 7 при x2

5,85

исходя из ее точного значения при

f x представляет

Решение:

Известно, что дифференциал dy функции y

собой главную часть приращения этой функции y .Если приращение аргумента x

мало по абсолютной величине, то приращение

приближенно равно дифференциалу, т.

е. y dy.

. Так как

y f x x f x , а

dy f

то имеет место приближенное

x dx,

равенство:

f x x f x f x x.

Пусть

x x ,

x x x

т. е.

x x

x .

Тогда

f x2 f x1 f x1 x2

x1 ,

или

f x2 f x1 f x1 x2

x1 .

(1)

Приближенное равенство (1) дает возможность найти значение функции при x x2 ,

если известно значение функции и ее производной при

x x1 .

Прежде чем

воспользоваться приближенным равенством ( 1 ) , находим числовое значение производной f'(x) при х= 6:

y 3x2 4x 7 1 ;

y	1	3x
		2
	3

Применяя (1), получаем

	2

4x 7	3

y 6

4 , или		y			6x 4	,


				33	3x2 4x 7 2
36 4		8	.
			.
75	15

y 5,85

3 5,85

4 5,85 7

4 6 7

5,85

6 5 0,08 4,92

3 6

Задача 4.

Найти

функции

z ln(x

)

Решение:

2x 0

ln x

y const

ln u

, где U x

ln x

0 2 y

2 y

x const

Задача 5. Найти полный дифференциал функции z = x3y + xtgx

Решение:

- теоретическая формула.

Где

	3
f x, y x	3	y xtgy	y
f x, y x		y xtgy	y
y

xf3 x

x
, y
cos	2

	3		2
x	3	y xtgy x 3x	2	y tgy
x		y xtgy x 3x		y tgy
y

											x
dz 3x		2 y tgy dx x3														dy							-ответ
dz 3x		2 y tgy dx x3											2			dy							-ответ
							cos						2	y
							cos							y
Задача 6. Вычислить приближённое значение																							z		x	2		y			2
																										2					2
точке P(2,97;4,02)
Решение:
	f x	0	x, y	0	y	f x					0	, y			0	f (x				; y		0	) x f	x			; y		0	y
		0		0							0				0		x		0			0		y	0				0
	2,97 3 0,03 x							0		3,						x 0,03
								0
т.Р											4,						y 0,02
т.Р		4,02 4 0,02 y							0		4,						y 0,02
									0
						f x, y											x	2	y		2	;
																		2			2

функции в

f x (x, y)			2x		x		;	f y	x, y			y		;


		2 x2 y 2			x2 y 2						x2	y 2
								3					4
Тогда	2,97 2	4,02 2		32 42				3		0,03			4		0,02


								42					32 42
						32		42					32 42

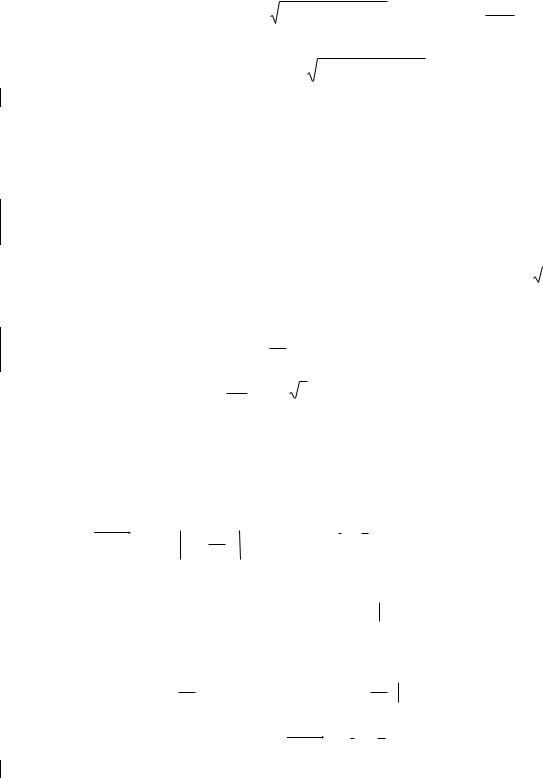
Или

2	4,02	2	5	0,09	0,08
2,97				5	5

Или

2	2	4,998
2,97	4,02	4,998

Задача 7.

Найти производную функции

z x

в направлении,

составляющим с положительным направлением оси (ОХ) угол =60 .

Решение:

cos

где и - углы наклона вектора

к оси

и к оси (OY)

соответственно.

cos cos60

;

cos cos30

;

=60, тогда =30

2 y,

тогда

3 y

- ответ.

Задача 8.

Вычислить градиент функции z x3 y3 3xy

в точке А (2;1).

Решение:

gradz	z		z
gradz	x	i	y	J
	x		y
	A			A

, где

- базисные векторы, орты.

z	3x	2	3y
		2
x

z	3y	2	3x
		2
y

z	3	22 3 1 12 3 9
x A

z	3	2	3 2 3 6 3
y	3	1	3 2 3 6 3
y
A

gradz 9i 3 j ответ

Задача 9. Найти смешанные частные производные второго порядка функции z x3 y2 x s

Решение:
		z	3x2 y 2 sin y				z	2x3 y x cos y
		x	3x2 y 2 sin y			y		2x3 y x cos y
		x				y
	z	по	y (x const),		2 z		6x2 y cos y
Дифференцируя,	x	по	y (x const),	получаем	x y		6x2 y cos y
Дифференцируя,	x			получаем	x y

Дифференцируя

по x (y=const), получаем

	2	z
	2
			6x	2	y cos y
y x			6x		y cos y
y x

		2	z		2	z
		2			2
							6x	2	y cos y
Ответ:	x	y		y x			6x		y cos y
Ответ:

Задача 10. Исследовать на экстремум функцию

z 3x 6y x	2	xy y	2

Решение: (1)

		z	0
		x	0
		x
		z
		z	0
		y	0
		y

- необходимое условие экстремума.

(2)

	2	z		2	z		2	z	2


		2			2				0,
x			y
		Po			Po	x y			Po

где

P	x	, y	0
0	0		0

является решением системы (1).

Неравенство (2) является достаточным условием экстремума.

Причём , если

	2 z
И если	x2
		Po

	2	x
	2
x
		2
0,

0,	то в точке				p0 x0 , y0 есть максимум функции.
Po
то в точке		P x		, y		есть минимум функции.
то в точке		0	0		0	есть минимум функции.
		0	0		0

Имеем:

z	3	2x y,
x

z 6 x 2 y;y

(1)

	3 2x y 0						P
							0
	6 x 2 y 0					P
							0
z				2	z
				2
2		2	y		2		2
		2	y		2		2
	Po				Po
	Po				Po
2			2 1			2	0
2			2 1				0

0;3 , т.е				x 0;	y 3
0;3 стационарная точка
		2	z
		2
				1
	x y
				Po
в	т.			P0 0;3	есть экстремум, причём т.к

	2	z
	2
x			2 0,
		2
			p
			0

то в точке P0(0;3) есть максимум

Ответ:

Z		3 0 6 3 0	2	0 3 3	2	9
			2		2
	max

Задача 11.

Найти наибольшее и наименьшее значения функции z x2 2y2 2x 8y 5 в

замкнутом треугольнике АОВ, ограниченном осями координат и прямой x + y -4=0 (рис.

12).

<<< < Предыдущая 1 2 34 / 114 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.11.20192.59 Mб14линия по пр-ву плавлен.сыра.doc
#
22.11.2019292.62 Кб9линия по сыру.docx
#
22.11.20195.47 Mб8линия по творогу.doc
#
14.04.2015135.17 Кб21лист достижения.doc
#
04.09.2019293.38 Кб13ЛР 3 Молотковые дробилки МШ Л.Р.№3.doc
#
14.04.20152.31 Mб39Математика 3 семестр.pdf
#
18.04.2019515.07 Кб12Мелиорация курсовая.doc
#
14.04.2015351.23 Кб97мелиорация.doc
#
23.09.201956.35 Кб5Менеджмент - методичка по курсовой.docx
#
14.04.201555.63 Кб7Мет указ по контр.раб для заочников.docx
#
22.11.2019108.54 Кб3МЕТЕОРОЛОГИЧЕСКИЕ ВЕЛИЧИНЫ.doc