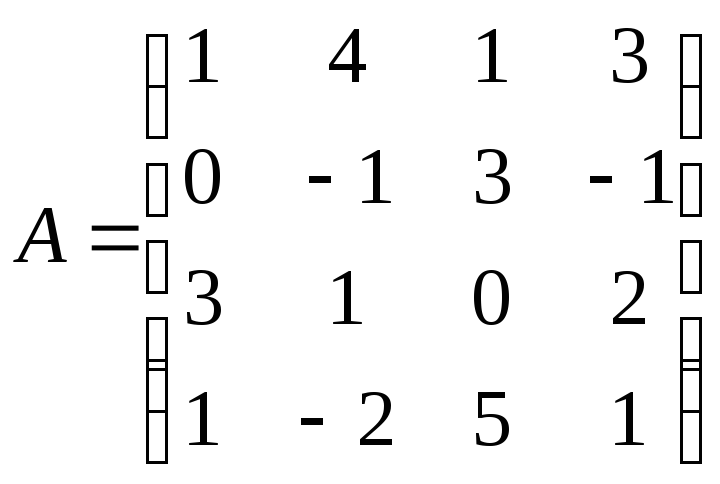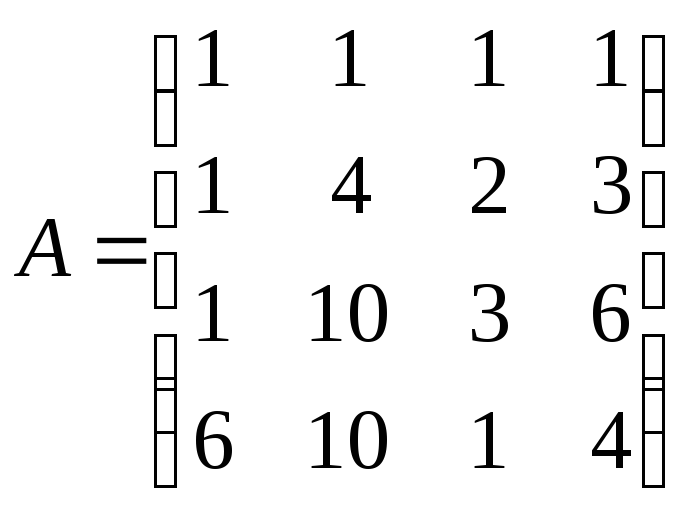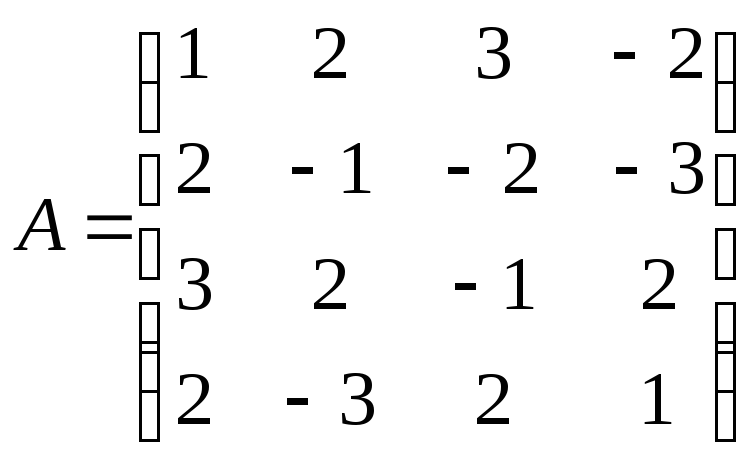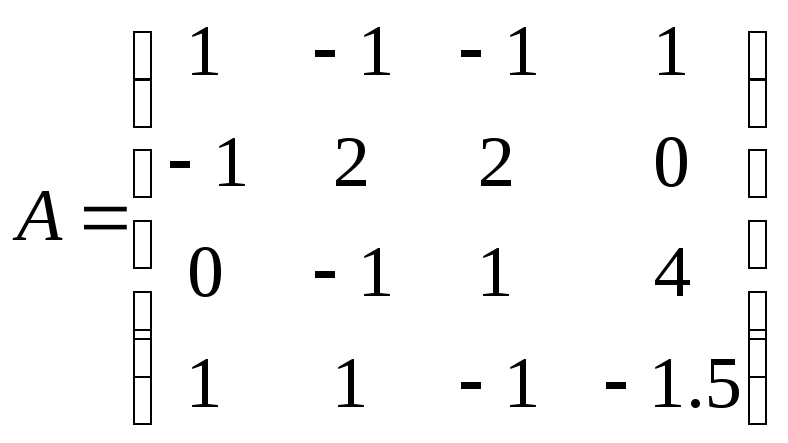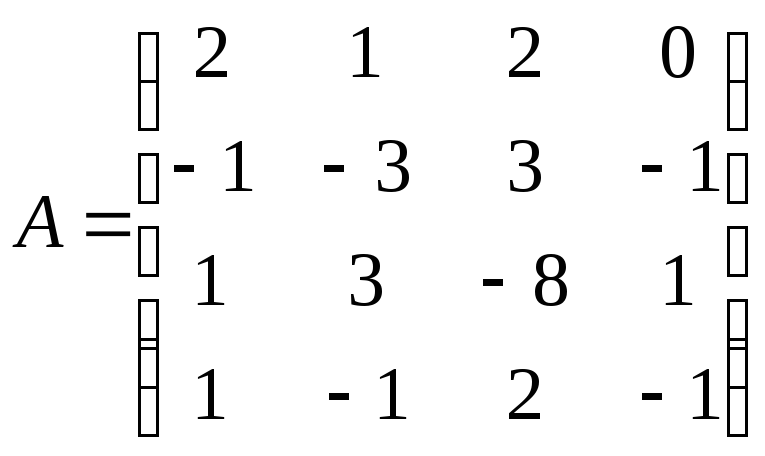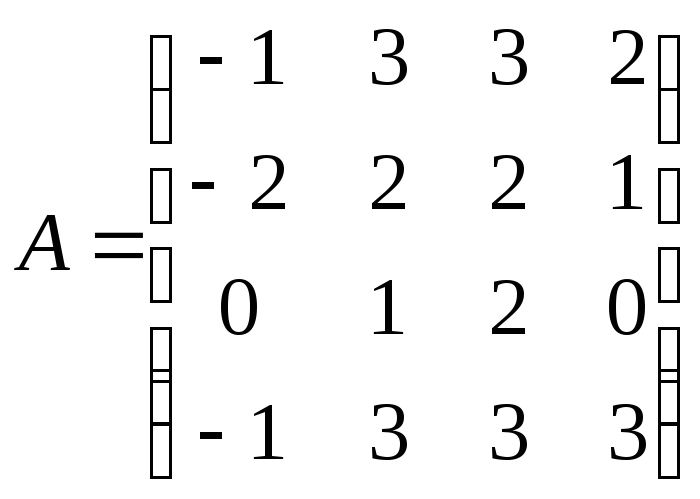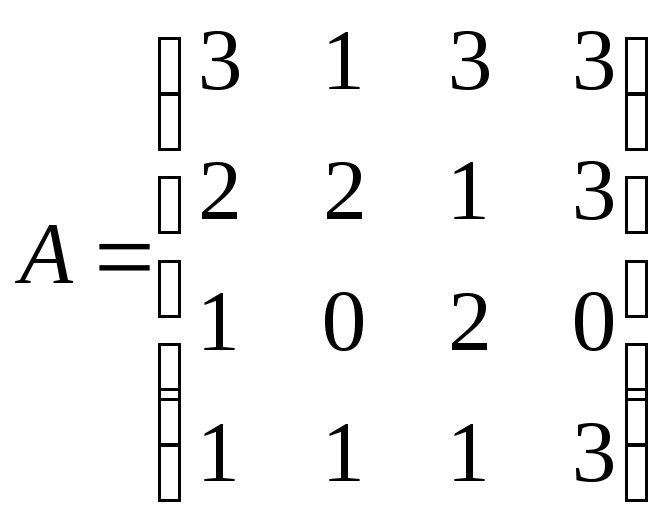Лабораторная работа № 15

Цель: изучить QR-алгоритм для нахождения собственных значений матрицы.

Задание

1. Разработайте класс «Полная проблема нахождения собственных значений» («CompleteProblem»), который наследуется от класса «Итерационные методы нахождения собственных значений» («IterationMethodsE»). В данном классе реализуйте QR-алгоритм («qrMethod») для нахождения собственных значений матрицы, используя метод для QR-разложения (QR_decomposition), описанный в классе «Алгоритмы факторизации» («FactorizationAlgorithms»).

Для реализации метода используйте объекты и методы матричных классов «SquareMatrix», «EMatrix», «Vector». Для выполнения основных матричных операций (перемножение матриц, вычитание матриц) используйте методы, реализованные в данных матричных классах.

2. Используя QR-алгоритм, найдите собственные значения матрицы в соответствии с вариантом.

3. Решите ту же задачу, используя пакет для математических вычислений.

4. Сравните результат выполнения п. 2 с решением, полученным в п. 3.

Варианты заданий

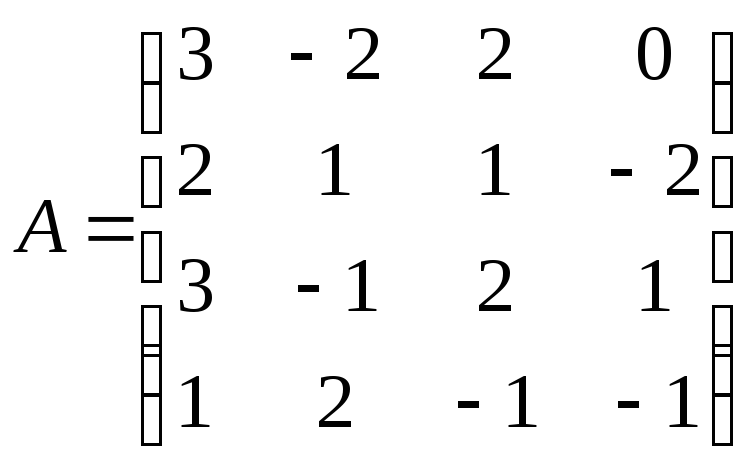
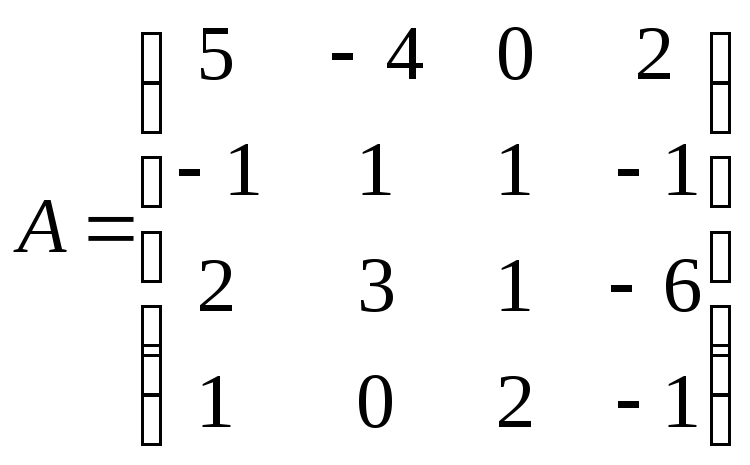
№ 1	№ 2
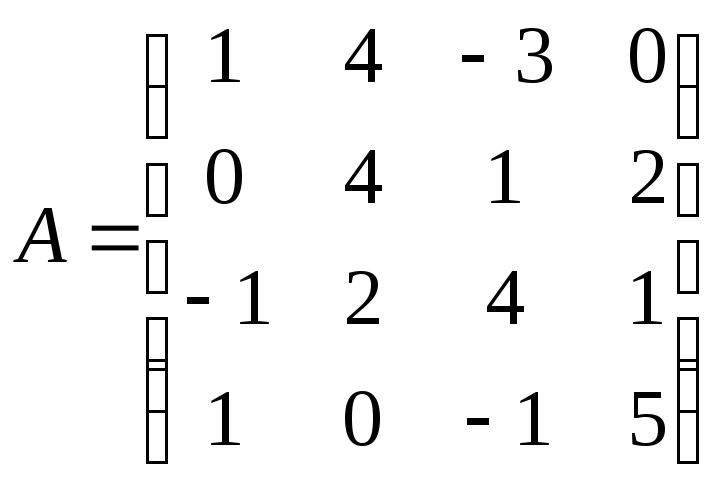
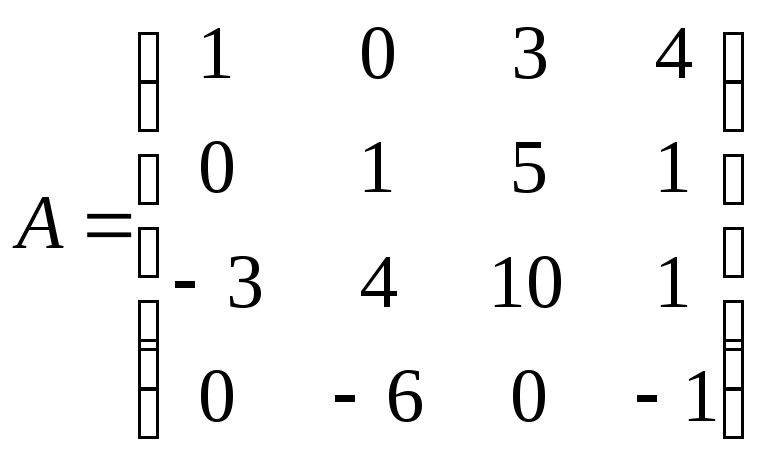
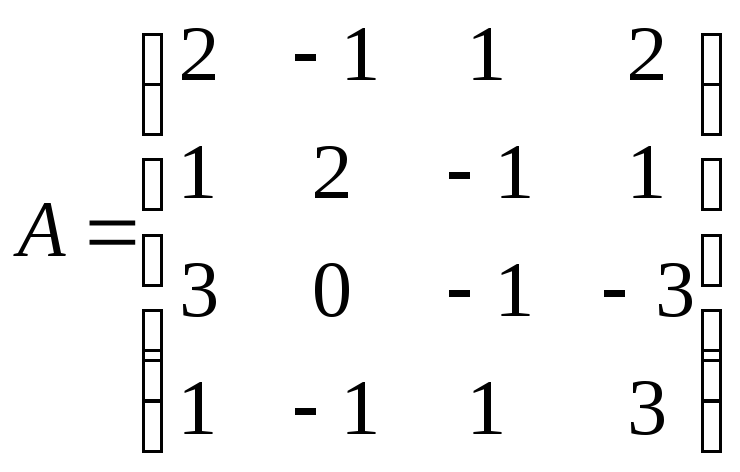
№ 3	№ 4
№ 5	№ 6
№ 7	№ 8
№ 9	№ 10
№ 11	№ 12
№ 13	№ 14
№ 15	№ 16

П 4.4 Метод Якоби для нахождения собственных значений и собственных векторов

Итерационный метод вращения (метод Якоби) решает полную проблему нахождения собственных значений и собственных векторов вещественной симметрической матрицы без использования характеристического уравнения.

Вычисление всех собственных значений и собственных векторов можно свести к отысканию такой ортогональной матрицы Т, для которой произведение представляет диагональную матрицу, причем столбцы матрицыТ будут являться соответствующими собственными векторами матрицы А. Матрица Т находится как предел бесконечного произведения элементарных матриц вращений, каждая из которых имеет вид [20]:

Если необходимо обратить в нуль элемент a_ik матрицы А, то cosφ и sinφ нужно выбрать по формулам

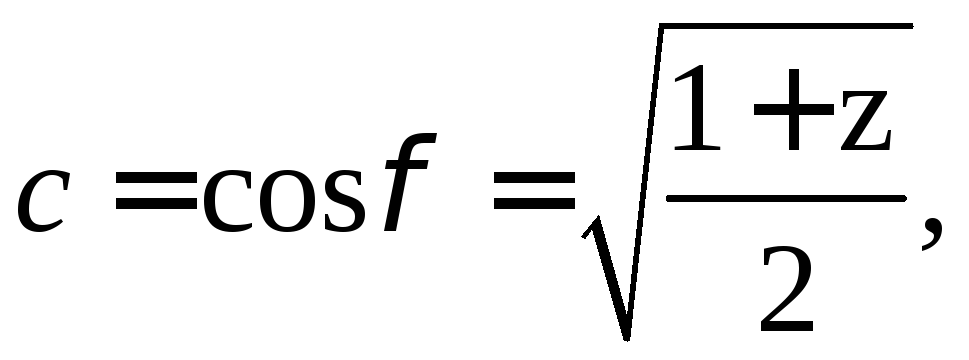
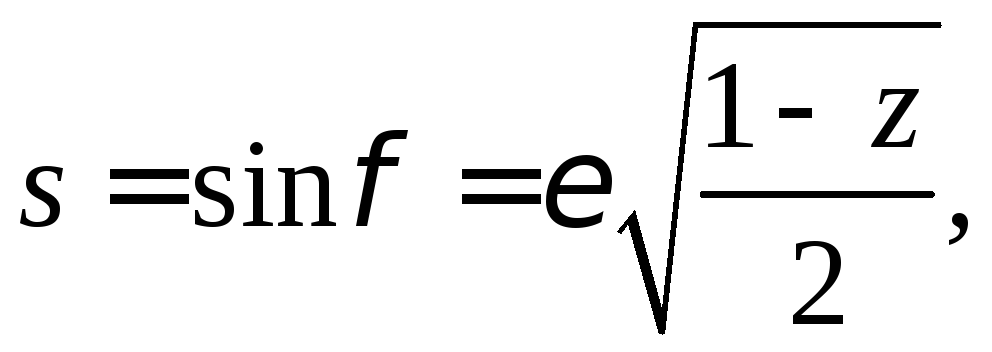(1)

где

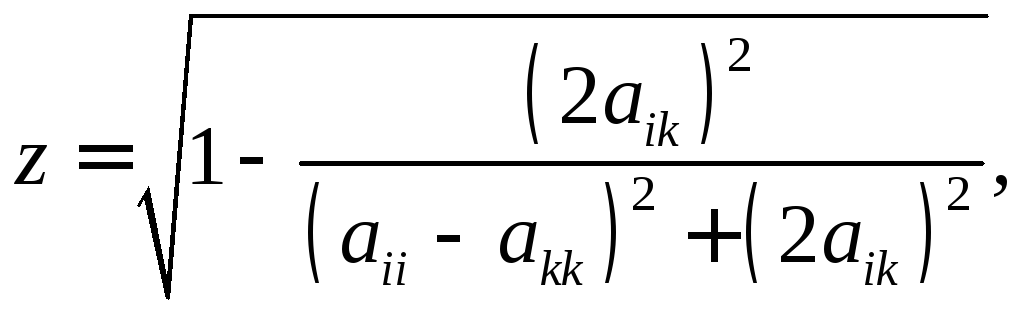
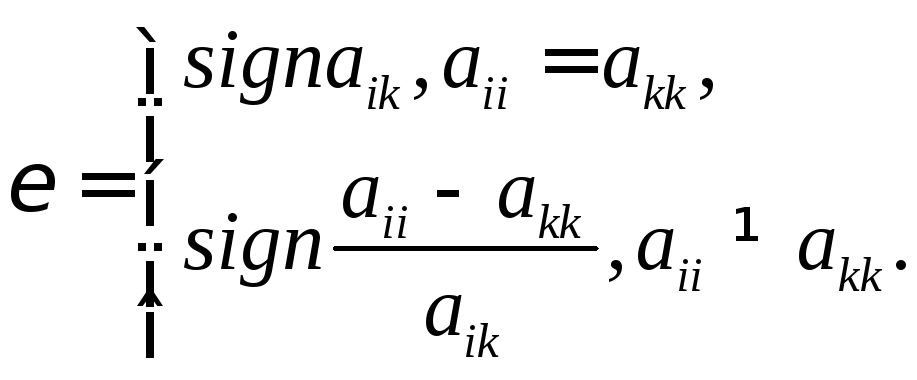
Тогда получим матрицу с измененнымиi-м и k-м столбцами и строками:

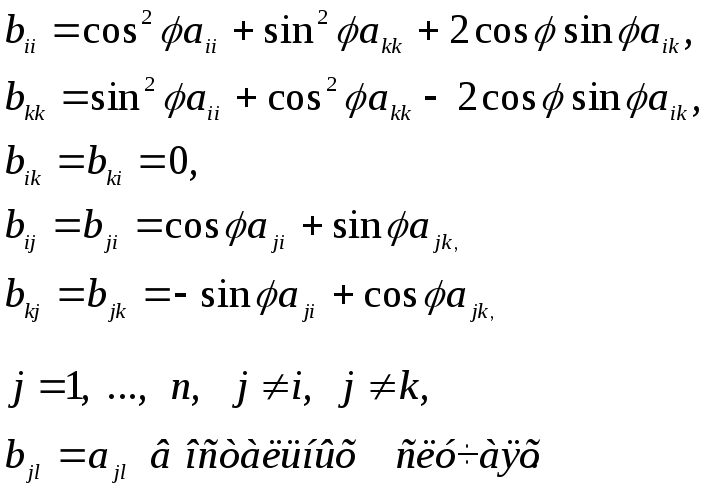(2)

Отметим, что выполняется соотношение =, т.е. сумма квадратов диагональных элементов увеличивается. Элементы, которые однажды обратились в нуль, при последующих шагах снова могут стать ненулевыми. Если на каждом шаге данного преобразования подобия брать максимальный по модулю наддиагональный элемент преобразуемой матрицы, то в пределе получится диагональная матрица. Исследование сходимости является сложным вопросом и в данном пункте не рассматривается.

Заметим, что по мере того, как А_m при m→∞ превращается в диагональную матрицу, на диагонали которой стоят собственные значения в некоторой последовательности, зависящей от выбранных вначале пар i, k, в столбцах матрицы появляются стоящие в соответствующей последовательности нормированные собственные векторы.

В качестве критерия окончания итерационного процесса используется условие малости суммы квадратов внедиагональных элементов [10].

Пример 1. Используя метод Якоби, найти собственные значения и векторы матрицы с точностью

.

Решение:

Выберем максимальный по модулю наддиагональный элемент матрицы А.

Пусть (i, k) = (1, 4), . По формулам (1) вычислимc и s:

c = 0,7245; s = 0,6892. Тогда матрица вращения будет иметь вид:

.

Матрица , вычисленная, согласно, будет иметь вид:

.

Первая итерация завершена.

Выберем максимальный по модулю наддиагональный элемент матрицы . Пусть (i, k) = (2, 3), . Проверим условие окончания итерационного процесса

,

следовательно, процесс необходимо продолжить. По формулам (1) вычислим c и s: c = 0,7733; s = 0,643. Тогда матрица вращения будет иметь вид:

.

Матрица , вычисленная, согласно, будет иметь вид:

.

Вторая итерация завершена.

Выберем максимальный по модулю наддиагональный элемент матрицы . Пусть(i, k) = (1, 2), . Условие окончания итерационного процесса не выполняется, переходим к следующей итерации. По формулам (1) вычислимc и s: c = 0,7989; s = 0,6015. Тогда матрица вращения будет иметь вид:

.

Матрица , вычисленная, согласно, будет иметь вид:

.

Продолжаем итерационный процесс до тех пор, пока не будет достигнута заданная точность наддиагональных элементов.

На двенадцатой итерации имеем:

.

Так как сумма квадратов наддиагональных элементов меньше , то процесс завершается.

На главной диагонали матрицы находятся собственные значения матрицыА:

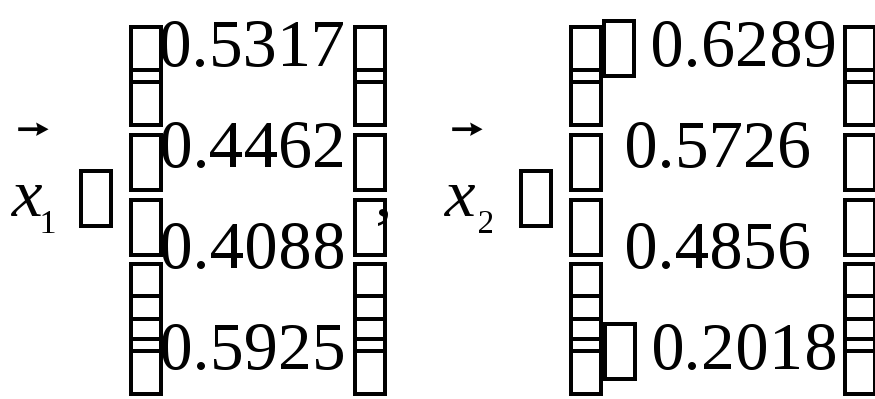
Столбцы матрицы являются собственными векторами матрицыА

.

, .
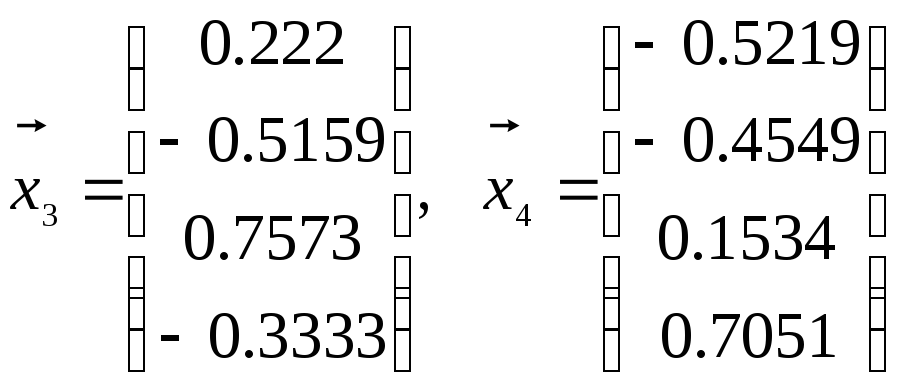