Лаб_практикум_ОВИ_03_06_13

Применение switch поясняет следующий пример:

function demswitch(x) a = 10/5 + x

switch a case -1

warning('a = -1') case 0

warning('a = 0') case 1

warning('a = 1') case {2, 3, 4}

warning('a равно 2 или 3 или 4') otherwise

warning('a не равно -1, 0, 1, 2, 3, 4')

end

»x = -4 demswitch(x) a = -2

»x = 1 demswitch(x) a = 3

Warning:a равно 2 или 3 или 4

Оператор прерывания цикла break

При организации циклических вычислений следует заботиться о том,

чтобы внутри цикла не возникло ошибок. Например, пусть задан массив x,

состоящий из целых чисел, и требуется сформировать новый массив y по правилу y(i) = x(i + 1) / x(i). Очевидно, что задача может быть решена при

131

помощи цикла for. Но если один из элементов исходного массива равен нулю, то при делении получится inf, и последующие вычисления могут оказаться бесполезными. Предотвратить эту ситуацию можно выходом из цикла, если текущее значение x(i) равно нулю. Следующий фрагмент программы демонстрирует использование оператора break для прерывания цикла:

for x = 1:20 z = x-8;

if z==0 break

end

y = x/z

end

Как только переменная z принимает значение 0, цикл прерывается.

Оператор break позволяет досрочно прервать выполнение циклов for

и while. Вне этих циклов оператор break не работает.

Если оператор break применяется во вложенном цикле, то он осуществляет выход только из внутреннего цикла.

6.2.Индивидуальные задания

1.Создайте М-файл mydemo.m.

2.Создайте в корневом каталоге диска D (или любом другом диске или каталоге, где студентам разрешено создавать свои каталоги) каталог со своей фамилией, например, WORK_IVANOV и запишите туда М-файл

mydemo.m под именем mydemo3.m. Установите пути к файлу и продемонстрируйте доступность файла из командной строки.

132

3.Постройте графики файл-функции myfun при помощи команд plot

иfplot на одних осях (при помощи hold on).

4.Напишите файл-функцию root2, которая находит только вещественные корни квадратного уравнения, а при наличии комплексных корней выдает сообщение об ошибке. В демонстрационных примерах второй коэффициент квадратного уравнения должен быть равен Вашему номеру по списку в журнале группы.

5.Напишите файл-функцию, которая находит наибольший общий делитель (НОД) z двух натуральных чисел x и y с помощью алгоритма Евклида. В одном из демонстрационных примеров наибольший общий делитель должен быть равен 3N+1, где N Ваш номер по списку в журнале группы.

Справочная информация. Идея алгоритма Евклида основана на том,

что если z НОД (x, y), то при равенстве чисел x и y НОД z совпадает с x и y, а в случае неравенства чисел x и y их разность между большим и меньшим вместе с меньшим числом имеет тот же самый наибольший общий делитель. Алгоритм определения НОД Евклида можно записать следующим образом:

Шаг 1. Если x > y, то перейти на шаг 4.

Шаг 2. Если x < y, то перейти на шаг 5, иначе перейти на шаг 3.

Шаг 3. z = x. Конец.

Шаг 4. Из x отнять y и считать, что эта разность теперь равна значению x. Перейти на шаг 1.

Шаг 5. Из y отнять x и считать, что эта разность теперь равна значению y. Перейти на шаг 1.

6. Напишите файл-функцию, которая находит простые числа, не превосходящие 150+10N, где N номер по списку в журнале группы.

Справочная информация. Простыми называются целые положительные числа, большие единицы, которые без остатка делятся только на самих себя и единицу. Одним из наиболее простых алгоритмов

133

получения простых чисел, не превосходящих n, является алгоритм Эратосфена, получивший название решета Эратосфена. Он состоит из следующих шагов:

Шаг 1. Выписать последовательно все целые числа, начиная с двух и

заканчивая n.

Шаг 2. Задаться числом p = 2.

Шаг 3. Если p2 n , то перейти на шаг 4, иначе перейти на шаг 6.

Шаг 4. В последовательности чисел, начиная с числа p + 1,

зачеркнуть все числа кратные p, не обращая внимания на то, что часть

последовательности считать новым значением числа p. Вернуться на шаг 3

алгоритма.

Шаг 6. Процесс окончен. Все незачеркнутые числа

последовательности являются простыми.

7.Вычислите сумму простых чисел, найденных в задании 6.

8.Оформите отчет по лабораторной работе.

134

Лабораторная работа 7

ИССЛЕДОВАНИЕ АЛГОРИТМА НЕЧЕТКОЙ КЛАСТЕРИЗАЦИИ

Цель лабораторной работы: получение и закрепление знаний про алгоритм нечеткой кластеризации, формирование практических навыков решения задач кластеризации методами нечеткой логики.

7.1.Краткие сведения из теории

7.1.1.FCM-алгоритм кластеризации

Алгоритм нечеткой кластеризации называют FCM-алгоритмом

(Fuzzy Classifier Means, Fuzzy C-Means). Целью FCM-алгоритма кластеризации является автоматическая классификация множества объектов, которые задаются векторами признаков в пространстве признаков. Другими словами, такой алгоритм определяет кластеры и соответственно классифицирует объекты. Кластеры представляются нечеткими множествами, и, кроме того, границы между кластерами также являются нечеткими.

принадлежности определяется расстоянием от объекта до

соответствующих кластерных центров. Данный алгоритм итерационно вычисляет центры кластеров и новые степени принадлежности объектов.

j – номер кластера, а k – номер входного вектора.

135

Принимаются во внимание следующие условия нормирования для

µjk:

N

jk 1, k 1,...,K;

j 1

N

0 jk K , j 1,...,N .

k 1

Цель алгоритма – минимизация суммы всех взвешенных расстояний

xk c j

N K

( jk )q xk c j min ,

j1k 1

где q – фиксированный параметр, задаваемый перед итерациями.

Для достижения вышеуказанной цели необходимо решить следующую систему уравнений:

Совместно с условиями нормирования µjk данная система уравнений имеет следующее решение:

(взвешенный центр гравитации) и

Алгоритм нечеткой кластеризации выполняется по шагам.

Шаг 1. Инициализация.

Выбираются следующие параметры:

–необходимое количество кластеров N, 2 < N < К;

–тип расстояний (например, расстояние по Евклиду);

–фиксированный параметр q (обычно 1,5);

–начальная (на нулевой итерации) матрица функций

принадлежности U ( 0 ) ( jk )(0) объектов хk ( k 1, K ) с учетом заданных начальных центров кластеров сj ( j 1, N ).

Шаг 2. Регулирование позиций c(jt ) центров кластеров.

На t-м итерационном шаге при известной матрице (jkt ) вычисляется

в соответствии с вышеприведенным решением системы уравнений.

Шаг 3. Корректировка значений принадлежности µjk.

Учитывая известные c(jt ) , вычисляются (jkt ) , если xk c j , в

противном случае:

Шаг 4. Остановка алгоритма.

137

Алгоритм нечеткой кластеризации останавливается при выполнении следующего условия:

7.1.2. Решение задач кластеризации

Существуют два способа решения задач кластеризации в MATLAB: с

использованием командной строки или графического интерфейса пользователя. Рассмотрим первый из указанных способов.

Для нахождения центров кластеров в MATLAB имеется встроенная функция fcm, описание которой представлено ниже.

Описание функции: [center,U,obj_fcn] fcm(data,cluster_n).

Аргументами данной функции являются:

1)data – множество данных, подлежащих кластеризации, каждая строка описывает точку в многомерном пространстве характеристик;

2)cluster_n – количество кластеров (более одного).

Функцией возвращаются следующие параметры:

1)center – матрица центров кластеров, каждая строка которой содержит координаты центра отдельного кластера;

2)U – результирующая матрица функции принадлежности;

3)obj_fcn – значение целевой функции на каждой итерации.

Пример 7.1. Программа нечеткой кластеризации.

//загрузка данных, подлежащих кластеризации, из файла

» load fcmdata.dat;

//определение центра кластеризации (два кластера)

138

» [center, U, obj_fcm] = fcm( fсmdata, 2); //определение максимальной степени принадлежности

//соответствующими кластерами

»index1 = find (U(1, :) == maxU);

»index2 = find(U(2, :) = maxU);

//построение данных, соответствующих первому кластеру

»plot (fcmdata (index1, 1), fcmdata (index1, 2),' ko', 'markersize', 5, 'LineWidth' ,1);

»hold on

//построение данных, соответствующих второму кластеру

»plot(fcmdata (index2, 1), fcmdata(index2, 2), 'kx', 'markersize', 5, 'LineWidth', 1);

// построение кластерных центров

»plot(center(1, 1), center(1, 2), 'ko', 'markersize', 15, 'LineWidth', 2)

»plot (center (2, 1), center (2, 2), 'kx', 'markersize', 15, 'LineWidth', 2)

На рис. 7.1 представлено множество данных, подлежащих кластеризации, и найденные центры кластеров для примера 7.1.

Функция fcm выполняется итерационно до тех пор, пока изменения целевой функции превышают некоторый заданный порог.

На каждом шаге в командном окне МАTLAB выводятся порядковый номер итерации и соответствующее текущее значение целевой функции

(табл. 7.1).

139

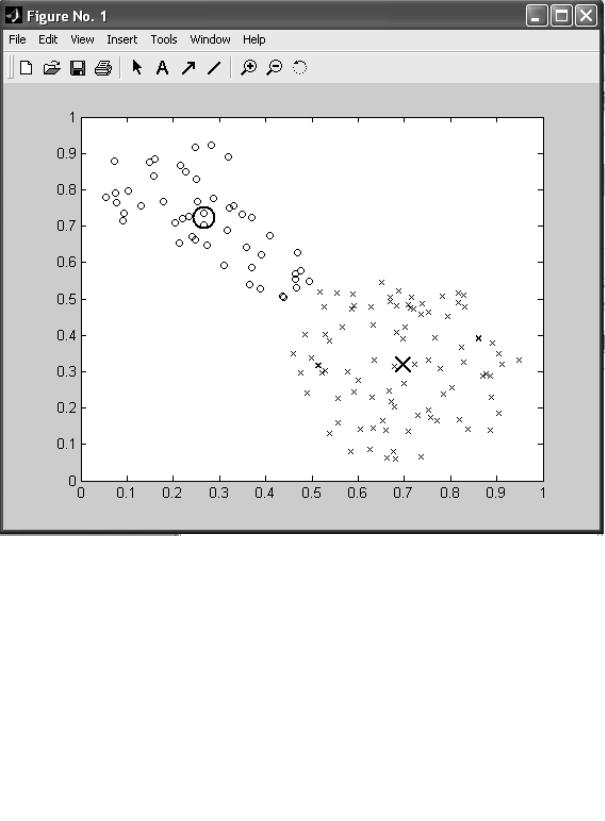
Рис. 7.1. Множество анализируемых данных и центры кластеров

Таблица 7.1 – Изменение целевой функции

Для оценки динамики изменения значений целевой функции используется команда построения графика plot(obj_fcm). Результаты примера 7.1 показаны на рис. 7.2.

140