
Нейронные сети Лаба 2
.pdf2 МОДЕЛИРОВАНИЕ ЛИНЕЙНЫХ СЕТЕЙ. РЕШЕНИЕ ЗАДАЧИ НАБЛЮДЕНИЯ ЗА НЕСТАЦИОНАРНЫМ СИГНАЛОМ
2.1 Цель работы
Освоение методик создания линейных нейронных сетей и настройки их параметров. Приобретение навыков решения задачи наблюдения за нестационарным сигналом.
2.2 Методические указания по организации самостоятельной работы студентов.
Рассматриваемые в данной лабораторной работе линейные нейронные сети по своей структуре аналогичны персептрону и отличаются только функцией активации, которая, в соответствии с названием, является линейной. Выход линейной нейронной сети может принимать любое значение, в то время как выход персептрона может быть только 0 и 1.
Настройка параметров осуществляется таким образом, чтобы обеспечить минимум ошибки. В случае использования критерия наименьших квадратов, поверхность ошибки как функции входов имеет один минимум, и нахождение глобального экстремума не составляет труда. В отличие от персептрона, настройка линейной сети может быть осуществлена не только путѐм адаптации, но и путѐм обучения. В этом случае используется правило обучения WH (Widrow - Hoff).
Кроме того, мы рассмотрим адаптирующиеся линейные нейронные сети ADALINE (ADAptive Linear Neuron networks), которые позволяют корректировать веса и сдвиги при получении на вход каждого нового элемента обучающего множества. Такие сети широко используются при решении задач обработки сигналов и в системах управления.
2.2.1 Архитектура линейной сети
Модель нейрона. На рис. 2.1 показан линейный нейрон с двумя входами. Его структура подобна структура персептрона, разница заключается лишь в функции активации – линейная PureLin вместо ступенчатой HardLim.

Входыи |
і ійний не |
рон |
|
Линейный нейрон |
|||
p1 |
w11 |
|
|
|
|
|
|
|
|
n |
a |
p2 |
w |
|
|
12 |
b |
|
|
|
1 |
|
a purelin (Wp b) |
Рисунок 2.1 – Линейный нейрон
Кроме передаточной функции, линейная сеть полностью определяется весовой матрицей W и вектором сдвигов b. В случае одного нейрона, W состоит только из одной строки, и выход сети определяется выражением
a purelin(n) purelin(Wp b) Wp b w11 p1 w12 p2 b.
Назначение функции PureLin — неискажѐнная передача сигнала. Это легко продемонстрировать на примере. Зададим функцию и произвольный сигнал:
import numpy as np import neurolab as nl
f = nl.trans.PureLin()
x = np.array([-100., 50., 10., 40.])
Функция возвращает то же, что и получает:
>>> f(x)
array([-100., 50., 10., 40.])
Таким образом, единственное воздействие, которое может произвести линейный нейрон на входной сигнал — это домножение на соответствующий вес и сдвиг. Этого достаточно, чтобы адаптивно решать задачи предсказания и восстановления сигнала.
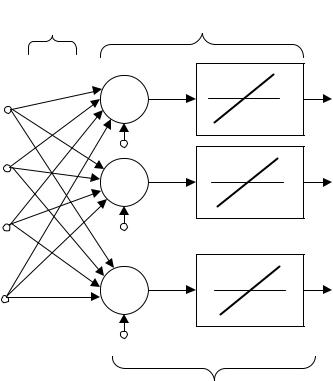
Архитектура сети. На рис. 2.3 показано, как несколько нейронов соединяются в однослойную сеть.
Входы |
Слой линейных нейронов |
|
|
|||
Входи |
Шар лінійних нейронов |
|
|
|||
w11 |
|
|
|
|
|
|
p1 |
|
n |
a |
|||
|
|
|
|
1 |
|
1 |
|
1 b1 |
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
n |
a |
2 |
||
|
|
|
|
2 |
|
|
p3 |
b |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
pR |
|
|
n |
S |
a |
S |
wSR |
|
|
||||
|
|
|
|
|||
|
|
|
|
|
|
|
|
bS |
|
|
|
|
|
|
1 |
|
|
|
|
|
a purelin (IW 11 p b1 )
Рисунок 2.3 – Архитектура сети
2.2.2. Создание модели линейной сети
Как было сказано выше, линейный нейрон является модификацией персептрона. Пользуясь аргументами функции создания персептрона, приведѐм его к виду, показанному на рисунке 2.1:
net = nl.net.newp( [ [-1,1],[1,1] ], 1, nl.trans.PureLin() )
Напомним, что первый аргумент задаѐт диапазон входных значений ([ 1,1] для первого входа, [ 1,1] для второго), второй аргумент указывает, что сеть состоит из одного нейрона, а третьим аргументом задана линейная функция активации этого слоя.
Попробуем задать веса и сдвиги вручную: net.layers[0].np['w'] = [[ 2, 3 ]] net.layers[0].np['b'] = [ -4 ]
Проверим правильность реакции сети на вход. При подаче сигнала p = [[ 5, 6 ]]
выход должен быть
a purelin(Wp b) w11 p1 w12 p2 b 2*5 3*6 ( 4) 24 .
Действительно
>>> net.sim(p) array([[ 24.]])
2.2.3 Обучение линейной сети
Для заданной линейной сети W ,b и соответствующего множества
векторов входа p и целей t можно вычислить вектор выхода сети
a purelin(Wp b) и сформулировать разницу между вектором входа и целевым вектором e t a , выразив таким образом погрешность. В процессе обучения необходимо найти такие значения весов W и сдвигов b, чтоб сумма квадратов соответствующих погрешностей была минимальной. Эта задача решаема, поскольку для линейных систем функция квадратичной ошибки является унимодальной (то есть существует единственный аргумент x*, для которого f(x) строго убывает при x x * и строго возрастает при x x *).
Как и для персептрона, используется процедура обучения с учителем, которая использует обучающие множества, где каждому вектору входа p1 , p2 , , pQ соответствует целевой выход t1 ,t2 , ,tQ .
Необходимо минимизировать следующую функцию средней квадратичной ошибки (mean square error):
|
1 |
N |
|
1 |
N |
|
|
MSE |
e(k)2 |
|
(t(k) a(k))2 . |
(2.2) |
|||
N |
N |
||||||
|
k 1 |
|
k 1 |
|
|||
|
|
|
|
|
Процедура настройки
В отличии от многих других сетей, настройка линейной сети при заданном обучающем множестве может быть выполнена при помощи прямого расчѐта.
Допустим, заданы следующие вектора обучающего множества:
{ 1, |
0.5}, |
что значит, что при подаче на вход 1 сеть должна вернуть 0,5, а |
{ 1.2, |
1} |
при подче -1,2 — единицу. Этого достаточно для формирования и обучения сети.
Во-первых, однослойная сеть может быть сформирована непосредственно под задачу, исходя только из параметров обучающей выборки:
P = array([[1],[-1.2]]) #входной сигнал T = array([[ 0.5],[1]]) #обучающий сигнал
Число входов сети и их диапазон задаѐтся на основании входных сигналов P (для их определения в пакете neurolab есть специальная функция minmax). Число выходов сети в случае единственного слоя равно количеству нейронов и равно размерности обучающего сигнала (последний элемент в кортеже shape(T)):
net = nl.net.newp(nl.tool.minmax(P), T.shape[-1], nl.trans.PureLin())
Таким образом, мы можем увидеть, что для решения данной задачи достаточно одного нейрона с одним входом и одним выходом.
Обучим сеть:
e = net.train(P, T, goal = 0.00)
Проверим результат:
>>> net.sim(P) array([[ 0.50038573],
[ 1.00016935]])
Выход соответствует целевому выходу с заданной точностью.
При этом сеть сформировала некоторый вес и сдвиг, обеспечивающий преобразование P T :
>>>net.layers[0].np['w'] array([[-0.22717437]])
>>>net.layers[0].np['b'] array([ 0.7275601])
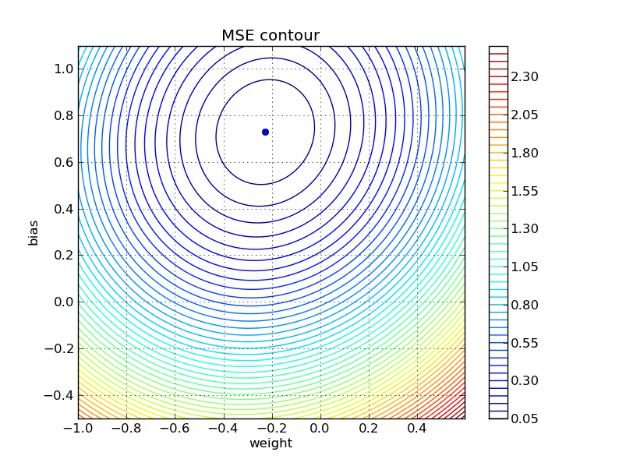
Для наглядности, мы можем построить поверхность погрешности сети как функцию от еѐ параметров. Отложив значения веса по одной оси и значения сдвига по другой, мы получим полное пространство состояний сети. Каждое точке в этом пространстве соответствует некоторая пара значений w и b, исчерпывающе описывающая сеть. Инициализируя сеть этими значениями, мы можем вычислить погрешность для данной обучающей выборке для любого состояния сети.
Приложив некоторые усилия для сбора данных об ошибке обучения на всѐм пространстве значений весов и сдвигов, мы можем построить карту ошибки. На рис. 2.4 по горизонтальной оси отложены значения веса, по вертикальной – значения сдвига, а каждая линия является изолинией, обозначающей определѐнный уровень ошибки.
Рисунок 2.4 – Уровни ошибки при разных значениях веса и сдвига. Исходный код в приложении.

Кружок отмечает найденные в ходе обучения значения веса и сдвига для данной обучающей выборки. Очевидно, что они предельно близки к оптимальным. Далее мы разберѐм, как происходит столь эффективное обучение.
Обучающее правило наименьших квадратов. Для линейной нейронной сети используется рекуррентное обучающее правило наименьших квадратов, которое намного эффективнее, чем обучающее дельта-правило персептрона. Правило наименьших квадратов или правило обучения WH (Уидроу-Хоффа) минимизирует среднее значение суммы квадратов ошибок обучения.
Авторы алгоритма допустили, что можно оценивать полную среднюю квадратичную погрешность, используя среднюю квадратичную погрешность на каждой итерации. Сформулируем частную производную по весам и сдвигам от квадрата погрешности на k -й итерации:
|
e2 (k) |
|
w1, j |
|
|
|
e2 (k) |
|
|
|
b |
|
2e(k) |
e(k) |
, |
j 1, , R; |
|
w |
|
(2.3) |
|
1, j |
|
|
|
|
|
|
2e(k) |
e(k) . |
|
|
|
b |
|
|
Подставляя выражение для ошибки в форме
|
|
R |
|
|
|
|
|
w1, j |
pi |
|
(2.4) |
e(k) t(k) |
(k) b , |
||||
|
|
j 1 |
|
|
|
получаем |
|
|
|
|
|
e(k) |
p j (k), |
|
|||
|
w1, j |
|
|
|
|
|
|
|
|
(2.5) |
|
|
e(k) |
|
|
|
|
|
1. |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
Здесь p j (k) — j -й элемент вектора входа на k -й итерации. Эти соотношения лежат в основе алгоритма WH
w(k 1) w(k) e(k) pT (k), |
(2.6) |
|
|
|
|
b(k |
1) b(k) e(k). |
|
Результат может быть обобщѐн на случай многих нейронов и |
||
представлен в матричной форме: |
|
|
W (k 1) W (k) 2 e(k) pT (k), |
(2.7) |
|
|
|
|
b(k 1) |
b(k) 2 e(k). |
|
Здесь ошибка e и сдвиг b - вектора, - параметр скорости обучения. При больших его значениях обучение происходит быстро, но чрезмерные его значения могут приводить к неустойчивости (выбиванию из экстремума). Для гарантии устойчивости процесса обучения, параметр скорости обучения не должен превышать величины 1 max( ) , где - собственное значение
матрицы корреляций p * pT векторов входа. Используя правило обучения
WH и метод ускоренного градиентного спуска, всегда можно обучить сеть так, чтоб еѐ погрешность была минимальной.
Программно реализован простой алгоритм настройки
|
|
dw lr e p , |
(2.8) |
|
|
db lr e, |
|
где lr - параметр скорости обучения.
Процедура обучения
Для обучения линейной сети применимы те же процедуры обучения, что и для персептрона.
Вернѐмся к тому же примеру, и выполним процедуру обучения, используя полученные знания:
lambd, norm = np.linalg.eig(P*transpose(P)) maxlr = 1/(max(abs(lambd)))
e = net.train(P, T, goal = 0.000, lr = 0.4*maxlr)
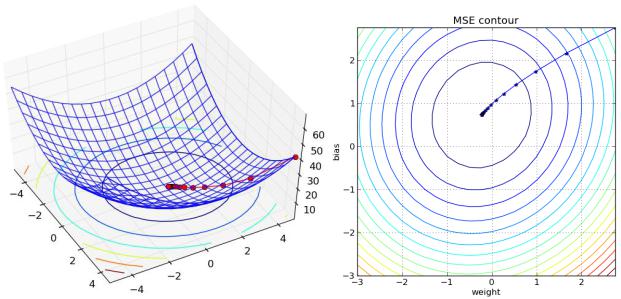
На рис. 2.5 построена поверхность функции критерия качества в пространстве параметров сети. Видно, как в процессе обучения состояние сети «скатывается» из точки начальной инициализации в точку минимума критерия ошибки.
Рисунок 2.5. Поверхность ошибки и траектория сети в процессе обучения (уровень ошибки обозначен высотой на левом графике и цветом,
аналогичным рисунку 2.4, на правом)
Подобные методы оптимизации называются градиентным спуском. Ясно, что их эффективность зависит от формы поверхности ошибки. Важно также понимать, что каждый новый параметр сети (вес или сдвиг) добавляет новое измерение в пространство поиска, поэтому при усложнении сети время обучения растѐт экспоненциально.

2.2.4 Наблюдение за нестационарным сигналом.
Рассмотрим задачу наблюдения нестационарного гармонического
сигнала, которая представляет реальный практический интерес. |
|
||||
Зададим |
дискретную |
выборку |
Т |
гармонического |
сигнала |
длительностью 6 секунд, частота которого увеличивается в 4 раза после 4 секунд. Частота квантования по времени для интервала 0-4 с. Составляет 20
Гц, а от 4,05 до 6 с. – 40 Гц.
time1 = np.arange(0,4,0.05) time2 = np.arange(4.05,6,0.0245)
time = np.concatenate((time1,time2)) T1 = sin(time1*4*pi)
T2 = sin(time2*8*pi)
T = np.concatenate((T1,T2))
У нас есть массив Т размера |
N TS , что соответствует групповой |
подаче данных. Превратим его в массив данных размерности 1 TS , |
|
содержащий последовательности N 1, |
что соответствует последовательной |
подаче данных: |
|
T.shape = (len(T),1) |
|
time.shape = (len(time),1) |
|
График гармонического сигнала приведен на рисунке 2.6.
Рисунок 2.6 – График гармонического сигнала
Поскольку при синтезе сети будут применяться адаптивные алгоритмы настройки, сформируем начальную последовательность {P,T} в виде массива, при этом последовательность входов должна совпадать с последовательностью выходов со сдвигом, т.к. рассматривается задача наблюдения.
Единичный сдвиг можно симулировать функцией np.roll(T,1), которая «прокручивает» массив T на единицу:
>>>np.roll([1,2,3,4,5], 1)
array([5, 1, 2, 3, 4])
То, что в первой позиции мы получаем значение последней, можно считать погрешностью или переходным процессом. Главное, что во второй позиции мы получаем первое значение.
Однако в реальных задачах обычно нельзя предсказать сигнал по одной точке, поэтому как правило в системах используется память. Это значит, что на вход сети подается несколько предыдущих значений, иными словами, используется несколько единичных задержек. Так, например, формируется память на три значения:
P = [np.roll(T,1), np.roll(T,2), np.roll(T,3)]
Чтобы этот сигнал был годен для подачи на вход сети, необходимо привести его к нужной размерности:
P = reshape(P,(len(P),len(T))) P = transpose(P)
Для решения поставленной задачи используем однослойную линейную сеть, которая предсказывает текущее значение сигнала по предыдущим пяти значениям.
Инициализация сети
Сеть состоит из одного нейрона с пятью входами, потому что на каждом шаге обрабатывается значение входного пяти запомненных точек сигнала P.
Создадим сеть:
net = nl.net.newp(nl.tool.minmax(P), T.shape[-1], nl.trans.PureLin())
Обратите внимание на параметры сети и их зависимость количества задержек.
Обучим сеть
e = net.train(P, T, goal = 0.1, show = 50, epochs = 500)
Проверка сети
Построим график полученного сигнала и сравним его с целевым:
plot (time,transpose(T),'--') plot (time, transpose(net.sim(P)))
pl.legend(['T','net.sim(P)'], loc = 0)
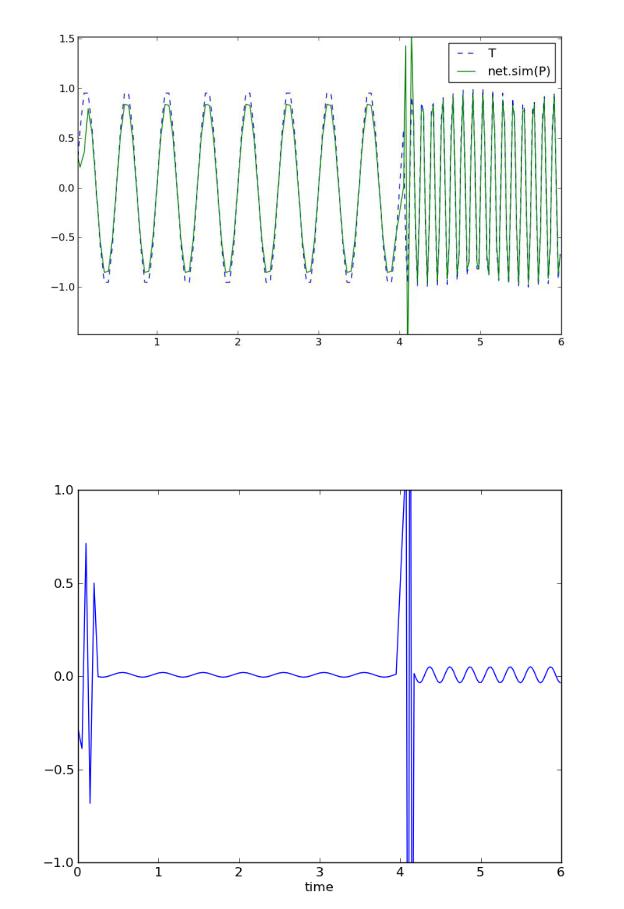
Рисунок 2.8 – График выходного и целевого сигналов
Для наглядности, приведѐм график разницы между входным сигналом и предсказанием сети (не путать с квадратичной ошибкой):
Рисунок 2.9 – Ошибка предсказания
