3. 3.3. Асимптотические соотношения оценки временной сложности

Как было показано ранее, время выполнения программы невозможно определить точно путем проведения серии экспериментов. Другой способ оценки временной сложности – математически оценить время исполнения подсчетом операций. Проиллюстрируем этот подход на примере задачи вычисления значения многочлена.

Задача вычисления значения многочлена.Дан многочлен степениn,

P_n(x) = a_nxⁿ + a_n-1x^n-1 + ... + a_ixⁱ + ... + a₁x¹ + a₀ ,(3.7)

заданный массивом своих коэффициентов A={A[0], A[1],…, A[n]}и значение переменнойx. Вычислить значение многочленаS = Pn(x).

Можно предложить следующий способ ее решения (алгоритм 1): для каждого слагаемого, кромеa₀возвестиxв заданную степень последовательным умножением и затем помножить на коэффициент. Затем слагаемые сложить. На рис. 3.4 приведена блок-схема этого алгоритма.

Рис. 3.4. Вычисления значения многочлена (алгоритм 1)

Для простоты анализа временной сложности Т(п) будем принимать в расчет только операции, связанные с вычислением значения многочлена игнорируя операции сравнения, инициализации и измения значений параметров цикла. Вычислениеi-го слагаемого(i=1..n) требуетiумножений. Значит, всего1 + 2 + 3 + ... + n = n(n+1)/2 умножений. Кроме того, требуетсяnсложений и одна операция начального присваивания значенияa₀. Таким образом, временная сложность этого алгоритма:Т(п) =n(n+1)/2 + n + 1 = n²/2 + 3n/2 + 1операций.

Теперь рассмотрим другой подход (алгоритм 2): в формуле (3.7) вынесемx-ы за скобки и перепишем многочлен в виде

P_n(x) = a₀ + x(a₁ + x(a₂ + ... ( a_i + .. x(a_n-1 + a_nx))). (3.8)

Расстановка скобок диктует такой порядок вычислений:

S₀ = a_n,

S₁ = S₀ x + a_n-1,

S₂ = S₁ x + a_n-2,

…,

S_i = S_i-1 x + a_n-i,

…,

Sn = Sn-1 x + a0, Pn(x) = Sn.

Рассмотренный метод называется схемой Горнера. На рис. 3.5 приведена блок-схема алгоритма вычисления значения многочлена по схеме Горнера.

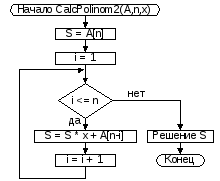
Рис. 3.5. Вычисления значения многочлена по схеме Горнера (алгоритм 2)

Подсчет временной сложности в этом случае гораздо проще: для вычисления S_iтребуется 1 умножение и 1 сложение. Всего такая итерация осуществляетсяnраз. Таким образом, временная сложность этого алгоритма:Т(п) =nумножений +nсложений =2nопераций.

Зачастую такая подробная оценка временной сложности не требуется. Вместо нее приводят лишь асимптотическую скорость возрастания количества операций при увеличении n.

Так, например, функция Т(п) = n²/2 + 3n/2 + 1возрастает приблизительно какn²/2(отбрасываем сравнительно медленно растущее слагаемое3n/2+1). Константный множитель1/2также убираем и получаем асимптотическую оценку для алгоритма 1, которая обозначается специальным символомO(n²)(читается как "О большое от эн квадрат"). Это – верхняя оценка, т.е количество операций (а значит, и время работы) растет не быстрее, чем квадрат количества элементов. В этом случае говорят, чтоТ(п) есть O(n²), илиТ(п) имеет порядок O(n²).

Чтобы почувствовать, что это такое, рассмотрим на таблицу 3.1, где приведены числа, иллюстрирующие скорость роста для нескольких разных функций.

Если считать, что числа в таблице соответствуют микросекундам, то для задачи с n=1048576элементами алгоритму с временем работы порядкаO(log n)потребуется 20 микросекунд, алгоритму со временем порядкаO(n)– 17 минут, а алгоритму с временем работы порядкаO(n²)– более 12 дней. Теперь преимущество алгоритма 2 с оценкойO(n)перед алгоритмом 1 достаточно очевидно.

Таблица 3.1

n	log2 n	n log2 n	n2
1	0	0	1
16	4	64	256
256	8	2 048	65 536
4 096	12	49 152	16 777 216
65 536	16	1 048 565	4 294 967 296
1 048 576	20	20 969 520	1 099 301 922 576
16 775 616	24	402 614 784	281 421 292 179 456

Наилучшей является оценка O(1). В этом случае время вообще не зависит отn, т.е постоянно при любом количестве элементов.

Таким образом, O( )– "урезанная" верхняя оценка временной сложности алгоритма, отражающая поведение этой сложности в пределе при увеличении размера задачи до бесконечности. Она называетсяасимптотической временной сложностью иливерхним порядком роста временной сложности.

Приведем математическое толкование символа O( ).

Определение 3.1.O(f(n))– множество функцийТ(п), для которых существуют такие константыcиn₀, чтоТ(п)  c f(n)для всехn  n₀. ЗаписьТ(п) = O(f(n))дословно обозначает, чтоТ(п)принадлежит множествуO(f(n)). Обратное выражениеO(f(n)) = Т(п)не имеет смысла.

В частности, можно сказать, что Т(п) = 50 nпринадлежитO(n²). Здесь мы имеем дело с неточной оценкой. Разумеется,Т(п)  50 n²приn  1, однако более сильным утверждением было быТ(п) = O(n), так как дляc=50и n₀ = 1верноТ(п)  cn, n  n₀.

Наряду с оценкой O(n)используется оценкаΩ(n)[читается как "Омега большое от эн"]. Она обозначает нижнюю оценку роста функции.

Определение 3.2.Ω(g(n))– множество функцийТ(п), для которых существуют такие константыcиn₀, чтоc g(n) Т(п) для всехn  n₀. В этом случае говорят, чтоТ(п)имеет нижний порядок роста g(n).

Например, пусть количество операций алгоритма описывает функция Т(п) = Ω(n²). Это значит, что даже в самом удачном случае будет произведено не менее порядкаn²действий. В то время как оценкаТ(п) = O(n³)гарантирует, что в самом худшем случае действий будет порядкаn³, не больше.

Также используется оценка Θ(n)[читается как "Тэта от эн"], которая является комбинацийO(n)иΩ(n). Она является точной оценкой асимптотики.

Определение 3.3.Θ(g(n))– множество функцийТ(п), для которых существуют такие константыc₁, c₂иn₀, чтоc₁ g(n) Т(п)  c₂ g(n)для всехn  n₀. ОценкаΘ(g(n))существует только тогда, когдаO(g(n))иΩ(g(n))совпадают и равна им.

Для рассмотренных выше алгоритмов вычисления многочлена временная сложность первого алгоритма порядка O(n²),Ω(n²)иΘ(n²), а второго – порядкаO(n),Ω(n)иΘ(n). Если добавить к первому алгоритму проверки наx=0в возведении в степень, то на самых удачных исходных данных (когдаx=0) имеем порядкаnпроверок, 0 умножений и 1 сложение, что дает новую оценкуΩ(n)вместе со старойO(n²). Как правило, основное внимание все же обращается на верхнюю оценкуO( ), поэтому, несмотря на "улучшение", алгоритм 2 остается предпочтительнее.

Итак, O( )– асимптотическая оценка алгоритма на худших входных данных,Ω( ) –на лучших входных данных,Θ( )– сокращенная запись одинаковыхO( )иΩ( ). Интуитивный смысл этих оценок:

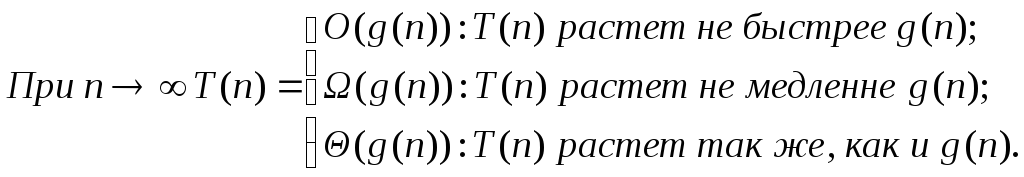(3.9)