Решения задач зкз ТАУ

14

Задача 1. Линеаризовать уравнение характеристики элемента умножения y=x₁x₂ в точке y₀=x₀₁x₀₂. Р е ш е н и е. В соответствии с малыми приращениями y₀+ Δy=(x₀₁+x₁)(x₀₂+x₂)= x₀₁x₀₂+x₀₁Δx₂+x₀₂Δx₁+Δx₁Δx₂= =y₀+x₀₁Δx₂+x₀₂Δx₁+ Δx₁Δx₂=y₀+x₀₁Δx₂+x₀₂Δx₁, пренебрегая малыми высшего порядка. Тогда вычитая значение y₀ из левой и правой частей, получим y= x₀₁Δx₂+x₀₂Δx₁= k₁Δx₁+k₂Δx₂, где k₁= x₀₂; k₂ =x₀₁, т.е. элемент умножения может быть приближенно представлен в виде сумматора и двух усилителей (линейных звеньев). Задача 2. Написать уравнения состояния и построить электронную модель системы, имеющей матрицы состояния: ; C=.

Р е ш е н и е. В соответствии с матрицами А,В и С уравнения состояния запишем в виде: Тогда электронная модель с использованием идеальных интеграторов и усилителей будет иметь вид:

Задача 3. Начертить блок-схему и написать уравнения состояния системы, описываемой дифференциальным уравнением , где g - входная величина; y - выходная величина. Р е ш е н и е. Разрешим уравнение относительно старшей производной и составим блок- схему ее получения рис.1

Рис.1 Блок-схема системы

В соответствии с выбранными переменными состояния на рис.2.8 запишем уравнения в нормальной форме

или в матричной форме где:

Задача 4. построить л.а.х. и л.ф.х. системы, описываемой передаточной функцией W(p)=100/(0.1p+1)(0.01p+1). Р е ш е н и е . Представим передаточную функцию в виде произведения элементарных звеньев Низкочастотный участок л.а.х. пойдет с наклоном 0 дБ/дек на уровне 20 lg 100= 40 дБ. Частоты сопряжения для апериодических составляющих будут соответственно ω₁=1/0.1=10 и ω₂=1/0.01=100. Фазочастотная характеристика строится в соответствии с уравнением Φ(ω)= arctg (0.1ω) + arctg (0.01ω). Ниже представлены графики л.а.х. и л.ф.х., соответствующие заданной передаточной функции.

Задача 5. Определить передаточную функцию минимально-фазового устройства, л.а.х. которого представлена ниже

Рис. 1. Логарифмическая амплитудночастотная характеристика устройства

Р е ш е н и е. Двигаясь по л.а.х. в направлении возрастания частоты определяем, что звено принадлежит к дифференцирующему типу, т.к. наклон низкочастотного участка равен +20дБ/дек (+1). Передаточная функция равна W(p)=0.2p. При частоте излома л.а.х. ω=50 наклон меняется на -20дБ/дек (-1). Очевидно добавлены два звена с передаточной функцией Тогда суммарная передаточная функция, соответствующая заданной л.а.х. будет иметь вид

Задача 6. Пользуясь правилами структурных преобразований привести представленную на рис.3.4. структурную схему замкнутой многоконтурной системы к одноконтурной и найти передаточные функции:

Рис.2. Структурная схема многоконтурной САУ

Р е ш е н и е: перед тем, как находить передаточные функции необходимо освободиться от перекрестных связей 1 и 2 на рис.3.4, для чего необходимо перенести или узел, или сумматор с добавлением соответствующих звеньев. Кроме того, целесообразно привести возмущающее воздействие f(t) ко входу САУ. Тогда получим схему на рис.3.5.

Рис.3.5. Преобразованная структурная схема без перекрестных связей

Пользуясь правилами структурных преобразований свернем внутренние контура и получим одноконтурную замкнутую САУ на рис.3.

Рис.3. Одноконтурная структурная схема САУ

Тогда требуемые передаточные функции замкнутой САУ запишем в виде:

Найденные с помощью правил структурных преобразований передаточные функции позволяют достаточно просто определить временные и частотные характеристики, а так же получить качественные и количественные оценки динамики и статики САУ.

Задача 7. Определить критический коэффициент усиления Ккр системы, разомкнутая передаточная функция которой . Р е ш е н и е. Найдем характеристическое уравнение замкнутой системы D(p) = p*(p² + p + 2) + k = p³ + p² + 2p + k = 0. Для системы третьего порядка граница устойчивости из определителя (минора) определятся правилом: произведение средних членов характеристического уравнения равно произведению крайних при положительном первом члене, т.е. 2*1=1*К_кр. Откуда К_кр=2.

Задача 8. Определить количество правых корней m системы третьего порядка, годограф Михайлова которой имеет вид

Р е ш е н и е. Из рисунка видно, что при изменении частоты от 0 до +ω суммарный угол поворота годографа Михайлова равен -. Тогда в соответствии с формулой (4.3) . Откуда число положительных корней m = 2.

Задача 9. Определить порядки астатизма по управляющему g(t) и возмущающему f(t) воздействиям САУ, структурная схема которой приведена на рис.5.11.

Рис.5.11. Структурная схема САУ

Р е ш е н и е. Сначала необходимо привести исходную структурную схеме к одноконтурной, как показано на рис.5.12.

Рис.5.12. Приведенная структурная схема

Из рис. 5.12 видно, что при охвате идеального интегратора отрицательной обратной связью получается апериодическое звено 1-го порядка. Поэтому пользуясь правилом определения порядка астатизма, приведенным выше, можно заключить, и по управляющему, и по возмущающему воздействию астатизм равен 1.

Задача 10. Определить предельное значение коэффициента передачи k нелинейного элемента из условия обеспечения абсолютной устойчивости нелинейной системы, передаточная функция линейной части которой

Р е ш е н и е. Амплитудно-фазовая характеристика линейной части

Тогда видоизмененная частотная характеристика

Изменяя частоту от 0 до построим видоизмененную частотную характеристику (рис.7.4).

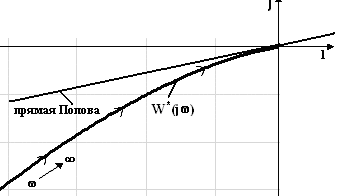Рис. 7.4. Видоизмененная частотная характеристика.

Вся характеристика W_лч*(jω) располагается во втором квадранте, поэтому линию (прямую) Попова предельную (наиболее близко подходящую к началу координат) можно провести через начало координат. В этом случае будет выполнятся условие, что вся видоизмененная а.ф.х. W*(jω) будет находится справа от прямой Попова. И предельный коэффициент нелинейного элемента К= находится из условия (1/К)=0, т.е. нелинейность для обеспечения абсолютной устойчивости может располагаться в угле arctg K=90°.

Задача 11. Определить возможную частоту автоколебаний при введении в САУ, имеющей ЛЧХ вида (рис.1), однозначной нелинейности в виде двухпозиционного реле.

Рис.1. ЛЧХ линейной части

Р е ш е н и е. Известно, что характеристика - 1/W_нэ(jω,А) однозначного нелинейного элемента (двухпозиционного реле) полностью располагается на отрицательной действительной полуоси, поэтому а.ф.х. линейной части W_лч(jω) может ее пересечь только при угле -180°. Частота возможных автоколебаний определяется по W_лч(jω), а л.ф.х. (рис.7.8) показывает, что фазовый угол сдвига -180° происходит на частоте ω = 300 рад/с. Это и есть возможная частота автоколебаний при введении в САУ однозначной нелинейности.

Задача 12. Изобразить фазовые траектории для нелинейной системы с тремя различными нелинейностями - двухпозиционное реле, трехпозиционное реле с зоной нечувствительности (±0,2) и двухпозиционное реле с гистерезисом (±0,1), если линейная часть имеет передаточную функцию . Примем для всех нелинейностей величину сигнала на выходе реле ±2. Р е ш е н и е. В соответствии с заданием модель нелинейной системы можно представить в виде рис.7.10.

Рис.7.10. Модель нелинейной САУ

Тогда уравнения состояния (7.9) запишутся в виде

Разделив второе из уравнений на первое, получим уравнение фазовой траектории

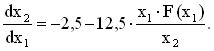
В зависимости от того, с какой стороны от линии переключения реле находится изображающая точка, решения дифференциального уравнения будут следующие [2]: справа от линии переключения при x₁ > 0 x₁ = 4 ln |x₂ + 10| - 0,4x₂ + c₁; cлева от линии переключения при x₁ < 0 x₁ = 4 ln |x₂ - 10| - 0,4x₂ + c₂; для трехпозиционного реле движение изображающей точки в пределах зоны нечувствительности -0,2<x₁<+0,2 соответствует уравнению x₁ = - 0,4x₂+c₃, где с₁, с₂ и с₃ - постоянные интегрирования, зависящие от начальных условий. На рис. 7.11 изображены фазовые траектории нелинейной САУ с различными нелинейными элементами. Припасовывание или сшивание участков фазовых траекторий происходит по линиям переключений.

Задача 13. На рис.7.13 представлены АФХ -1/W_нэ(A) и W_лч(jω). Кроме того в нее вводится звено чистого запаздывания. Определить критическое время чистого запаздывания, при котором в нелинейной системе возникают автоколебания.

Рис.7.13. АФХ нелинейности -1/W_нэ(A) и линейной части W_лч(jω)

Р е ш е н и е. Известно, что звено чистого запаздывания меняет только фазовый сдвиг и не меняет амплитуду сигнала. Ближайшее расстояние АФХ обратной передаточной функции нелинейного элемента от начала координат равно (-1). Модуль АФХ линейной части, равный единице, приобретает свое значение на частоте ω_ср = ω_кр = 6,28. Запас по фазе равен φ_кр= φ_зап= -90°=-π/2. Тогда τ_кр = φ_кр/ω_кр = 0,25 c.

Рис. 7.11. Фазовые траектории релейных систем

Анализируя фазовые траектории, можно сделать следующие выводы: 1. при взятых начальных условиях все системы устойчивы. Причем системы с двухпозиционными реле устойчивы "в большом"; 2. у систем с двухпозиционными реле наблюдаются устойчивые колебания. Абсцисса предельного цикла определяет амплитуду колебаний А_о, а частота может быть определена из ординаты предельного цикла А_оω_о; 3. система с трехпозиционным реле с зоной нечувствительности имеет "особый отрезок". Система может после прохождения переходного процесса занять любое значение внутри зоны нечувствительности, как показано на рис.7.11.

Задача 14. Определить дискретную передаточную функцию системы, непрерывная часть которой состоит из ПИ - регулятора и нейтрального объекта , а в качестве импульсного элемента используется экстраполятор нулевого порядка и экстраполятор с АИМ 1-го рода. Принять период дискретности Т₀=2с, общий коэффициент усиления К=20 с^-2, посто-янную времени τ=5 с, импульсы длительности γ=0,2 с. Р е ш е н и е . В соответствии с формулой (8.7) передаточная функция цифровой системы (экстраполятор нулевого порядка)

В соответствии с таблицами z - преобразований [2,6] находим

В соответствии с формулой (8.10) передаточная функция импульсной системы (экстраполятор с АИМ 1-го рода)

В соответствии с таблицами z - преобразований находим

Как видим, передаточные функции импульсной системы в значительной степени зависят от вида и параметров экстраполяторов, что необходимо

Задача 15. Построить логарифмические частотные характеристики импульсной системы с экстраполятором нулевого порядка, период дискретности которой T_o=2с, а передаточная функция непрерывной части

.

Р е ш е н и е . Выбираем частоту среза ω_cр<2/T_o<1 c^-1. В соответствии с заданными постоянными времени для непрерывной части определяем сопрягающую частоту ω_cопр1=1/5=0.2 ^c-1 - низкочастотный диапазон. В соответствии с уравнением (8.18) передаточная функция от псевдочастоты будет иметь вид:

, где = 0.

В соответствии с уравнением (8.19) фазочастотная характеристика будет иметь вид:

На рис.8.9 представлены асимптотические ЛЧХ, соответствующие λ_ср=ω_ср=0,5; λ_сопр1=ω_сопр1=1/5=0,2; λ_сопр2=1/1=1. Коэффициент усиления К может быть выбран из условия прохождения среднечастотного участка через λ_ср с наклоном -20 дБ/дек.

Рис. 8.9. ЛЧХ импульсной системы

Задача 16. Дать заключение об устойчивости импульсной системы, характеристическое уравнение которой D(z)=10z³+4z²+6z+2+0. Р е ш е н и е. Для ответа на поставленный вопрос воспользуемся билинейным преобразованием, т.е. сделаем подстановку в характеристическое уравнение (8.11)

Тогда получим характеристическое уравнение от w D(w)=5w³ + 13w² + 11w + 11=0. Используя критерий Гурвица на основании линейной ТАУ для системы третьего порядка необходимым и достаточным условием устойчивости является произведение средних членов характеристического уравнения должно быть больше произведения крайних, т.е. 11*13 - 5*11 = 88>0. Таким образом импульсная система устойчива.

Задача 17. Написать разностное уравнение, связывающее выходную координату y[nT] и входное воздействие x[nT] импульсной системы, передаточная функция которой

Р е ш е н и е. В соответствии с дискретной передаточной функцией первоначально надо составить структурную схему в виде одной из форм рис.1. Представим заданную W(z) в форме 1

Домножим числитель и знаменатель W(z) на z^-2. В результате получим

Разностное уравнение имеет вид: y[n] -2y[n-1] +y[n-2] = 240 x[n-1] -160 x[n-2]. Тогда выходная переменная может быть получена, как (при нулевых начальных условиях) y[n] = 2y[n-1] -y[n-2] + 240 x[n-1] -160 x[n-2]. В соответствии с последним уравнением расчетная структурная схема представлена на рис.8.14

Рис.1. Расчетная структурная схема импульсной системы

Задача 18. Определить скоростную ошибку регулирования импульсной системы при подаче на вход управляющего воздействия g(t)=g₁t, если ее разомкнутая передаточная функция

Период квантования Т_о=2 с. Р е ш е н и е. В соответствии с формулой (8.22) и таблицей z - преобразований для линейно нарастающего сигнала, получим

Этот результат вполне закономерен, так как система обладает астатизмом второго порядка.

Задача 19. Пусть передаточная функция разомкнутой системы W(p)=k/(p(Tp+1)). На САУ подается полезный сигнал g(t)=g₁t и помеха "белый шум" со спектральной плотностью S_f(ω)=N. Определить систематическую ошибку m_ε и среднеквадратическую ошибку σ. Структурная схема представлена на рис.1.

Рис.1. САУ со случайным сигналом

Р е ш е н и е. Систематическая ошибка определяется с применением коэффициентов ошибок

Тогда m_ε=0*g₁t + g₁(1/k)=g₁/k.Дисперсия ошибки по формуле (9.20)

Для системы второго порядка величина интеграла J2 вычисляется по формуле [2,19]

где т.е. b_o=0; a₂=k; b₁=k; a₀=T; a₁=1. Очевидно D_ε=Nk/2 или .

Из полученных результатов следует, что увеличение общего коэффициента передачи разомкнутой цепи системы k с одной стороны ведет к уменьшению установившегося значения систематической ошибки системы m_ε. В тоже время, для уменьшения дисперсии ошибки, вызванной помехой на входе, необходимо, чтобы значение общего коэффициента передачи разомкнутой цепи системы k было минимально.

Задача 20. Оценить свойства управляемости и наблюдаемости САУ, заданной уравнениями состояния

где:

Р е ш е н и е. Находим матрицу управляемости N_У=[B | AB]

Так как ранг r=2=n , то система полностью управляема. Находим матрицу наблюдаемости N_Н=[C^T | (CA)^T]

Так как ранг r=2=n, то САУ полностью наблюдаема.

Задача 21 . Определить управляемость САУ третьего порядка n=3 с одним управляющим воздействием m=1, представленных уравнениями состояния x=Ax + Bu с матрицами системы А и В вида

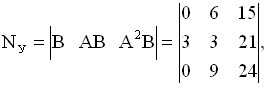Р е ш е н и е. Тогда матрица управляемости det(N_y)=-27, rang(N_y)=n=3, т.е. система управляема.