Лекция 21

21.1. Двойные интегралы

21.1.1. Определение двойного интеграла

Пусть в области D, ограниченной некоторой линией , задана произвольная непрерывная функция z=f(x,y). Разобьем область на достаточно большое число элементарных площадок достаточно малого размера системой линий. Перенумеруем их произвольным образом. Обозначим площадь элементарных площадок S₁, S₂, S₃,..., S_n. Выберем на каждой элементарной площадке S_i точку M_i(_i,_i) S_i, i=1,2,...,n. Вычислим в каждой из точек значение z_i=f(M_i )= f(_i,_i). Назовем диаметром элементарной площадки величину наибольшего отрезка, проходящего через элементарную площадку. Обозначим его d_i. Обозначим maxd_i=. Начнем строить различные интегральные суммы так, чтобы 0 и, соответственно, n.

Определение. Предел интегральных сумм вида (1) при 0, если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора значений M_i(_i,_i) S_i на этих частях, называется двойным интегралом в области D от функции z=f(x,y) по dxdy. Обозначается

(2)

Замечание. Если разбивать на части область D прямыми x=const, y=const, то элементарные области, не имеющие пересечения с границами, имеют вид прямоугольников, а их площадь равна S_k=x_i y_j. Поэтому двойной интеграл обозначают

(3)

21.1.2. Повторные интегралы и вычисление двойного интеграла

Пусть нам дан интеграл (3). Рассмотрим вначале случай, когда в области D, ограниченной некоторой линией , задана непрерывная функция z=f(x,y) такая, что f(x,y)0. Назовем область D правильной по оси Ox, если каждая прямая, лежащая внутри области D параллельная оси Oy, пересекает границу области не более, чем в двух точках. Спроектируем область D на ось Ox в отрезок [a,b]. Для этого через каждую точку области D проведем проектирующую прямую. Множество концов прямых, входящих в область D, т. е. нижних концов, лежащих на границе , задают функцию. Обозначим ее y=(x). Множество концов прямых, выходящих из области D, т. е. верхних концов, лежащих на границе , задают функцию y=(x). Иллюстрация дана на рис. 3. Возьмем значение x=[a,b], и проведем плоскость, параллельную плоскости Oyz. Получим сечение тела этой плоскостью. Обозначим площадь сечения S=Q(). Тогда объем тела V равен

Площадь сечения равна

Тогда

Интеграл, стоящий в правой части, называется повторным.

y

y=(x)

y=(x)

O a b x

Рис. 3. Проектирование области D на ось Ox

y

d

y=₁(x) y=₁(x)

c

O a b x

Рис. 4. Проектирование области D на ось Oy

Аналогично, спроектируем правильную по оси Oy область D на ось Oy в отрезок [c,d]. Для этого через каждую точку области D проведем проектирующую прямую, параллельную оси. Множество концов прямых, входящих в область D, т. е. левых концов, лежащих на границе , задают функцию. Обозначим ее x =₁(y). Множество концов прямых, выходящих из области D, т. е. правых концов, лежащих на границе , задают функцию x =₁(y). Тогда

Если область D неправильная, то разобьем ее на несколько правильных частей.

Теорема. Если функция z=f(x,y) непрерывна в области D и интеграл (2) существует, то он равен повторному. (Без доказательства).

Пример. Вычислить интеграл

где область D ограничена линиями

Решение. Изобразим область D и сведем интеграл к повторному.

y

y=x

x² – 2x + y² = 0

O 2 x

21.1.3. Замена переменных в двойных интегралах

Часто при вычислениях двойных интегралов полезно применять замену переменных. Рассмотрим прием замены на примере перехода к полярным координатам. Пусть задана прямоугольная декартова система координат Oxy. Выберем полюс в начале координат и полярную ось, проходящую по оси Ox. Точка M(x,y) в полярной системе имеет координаты M(,). Переход от полярной системы к декартовой формулой

(4)

Обратный переход

(5)

Пусть нам дан интеграл

y

 r=r₂()

 r=r₁()

x

Рис. 1. Разбиение области в полярных координатах

Перейдем к полярным координатам. Замена переменных дается формулой (4). Разобьем область (см. рис. 1) на элементарные площадки системой линий =const, =const. Система линий =const задает систему концентрических окружностей с центром в начале координат, система линий =const задает систему лучей, выходящих из начала координат. Обозначим систему линий =_i =_j и рассмотрим элементарную площадку. Очевидно, что

Получим

где область D та же область D, но заданная в полярных координатах.

Для перехода к повторному интегралу проведем через каждую точку области D лучи, выходящие из начала координат. Множество концов лучей, входящих в область D, задают часть границы области, уравнение которой имеет вид r=r₁(). Множество концов лучей, выходящих из области D, задают часть границы области, уравнение которой имеет вид r=r₂(). Предельные положения лучей, проходящих через область, задают углы = и =. Тогда

Пример. Вычислить интеграл

где D область, граница которой задана линией и условием

Изобразим область (см. рис. 2) и перейдем к полярным координатам

y

O x

Рис. 2. Область интегрирования для данной задачи

Получим

21.2. Тройные интегралы

21.2.1. Определение и существование тройного интеграла

Пусть в области V, ограниченной некоторой поверхностью S, задана непрерывная функция u=f(x,y, z). Выберем прямоугольную декартову систему координат Oxyz. Построим тело V. Разобьем область V на достаточно большое число частей достаточно малого размера системой поверхностей. Назовем эти части элементарными объемами и перенумеруем их произвольным образом. Обозначим объем элементарных объемов V₁, V₂, V₃,..., V_n. Выберем в каждом элементарном площадке V_i точку M_i(_i,_i,_i) V_i, i=1,2,...,n. Вычислим в каждой из точек значение u_i=f(M_i )= f(_i,_i,_i). Вычислим для каждого элементарного объема значение m_i = f(M_i ) V_i = f(_i,_i,_i) V_i. Назовем диаметром элементарного объема величину наибольшего отрезка, проходящего через элементарную площадку. Обозначим _i диаметр элементарного объема. Обозначим max_i=. Начнем строить различные интегральные суммы так, чтобы 0 и, соответственно, n.

Определение. Предел интегральных сумм вида (1) при 0, если этот предел существует и не зависит ни от способа разбиения области V на части, ни от выбора значений M_i(_i,_i,_i) V_i на этих частях, называется тройным интегралом по области V от функции u=f(x,y, z) по dxdydz. Обозначается

(2)

21.2.2. Повторные интегралы и вычисление тройного интеграла

Пусть нам дан интеграл (2). Рассмотрим вначале случай, когда в области V, ограниченной некоторой поверхностью S, задана непрерывная функция u=f(x,y,z) такая, что f(x,y,z)0. Предположим, что область V правильная. Это значит, что каждая прямая, параллельная оси Oz, пересекает границу области не более, чем в двух точках. Спроектируем область V на плоскость Oxy в область D. Для этого через каждую точку области V проведем проектирующую прямую. Множество концов прямых, входящих в область V, т. е. нижних концов, лежащих на границе S, задают некоторую функцию. Обозначим ее z =(x,y). Множество концов прямых, выходящих из области V, т. е. верхних концов, лежащих на границе S, задают функцию z= (x,y). Иллюстрация дана на рис. 9.2.

Теорема. Тройной интеграл равен

(Без доказательства).

Интеграл, стоящий в правой части, называется повторным.

Спроектируем область D на ось Ox в отрезок [a,b]. Для этого через каждую точку области D проведем проектирующую прямую, параллельную оси Oy. Множество концов прямых, входящих в область D, т. е. нижних концов, лежащих на границе , задают функцию y=₁(x). Множество концов прямых, выходящих из области D, т. е. верхних концов, лежащих на границе , задают функцию y=₁(x).

Тогда

Аналогично, можно провести проектирование в другой последовательности.

Пример. Вычислить интеграл

где область V ограничена линиями

Решение. Изобразим область V и сведем интеграл к повторному.

21.2.3. Замена переменных в тройных интегралах

Часто при вычислениях тройных интегралов полезно применять замену переменных. В общем случае замена задается в виде

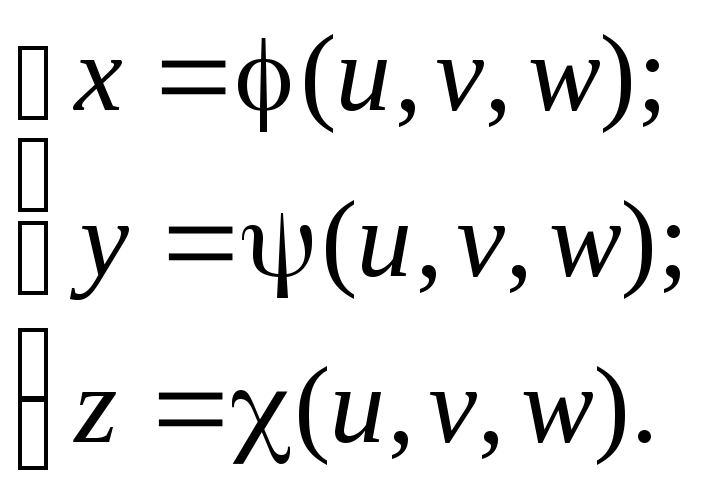
Введем величину, которая называется якобианом

Тогда

Чаще всего используют переход к цилиндрическим и сферическим координатам. Переход к цилиндрическим координатам задается формулами

(4)

Пусть нам дан интеграл. Тогда

Переход к сферическим координатам задается формулами

(5)

Пусть нам дан интеграл. Тогда