10. Алгоритм RSA.

RSA – криптографическая система открытого ключа, обеспечивающая такие механизмы защиты как шифрование и цифровая подпись (аутентификация – установление подлинности). Криптосистема RSA разработана в 1977 году и названа в честь ее разработчиков Ronald Rivest, Adi Shamir и Leonard Adleman. Алгоритм RSA работает следующим образом: берутся два достаточно больших простых числа p и q и вычисляется их произведение n = p*q; n называется модулем.

Затем выбирается число e, удовлетворяющее условию

1< e < (p - 1)*(q - 1) и не имеющее общих делителей кроме 1 (взаимно простое) с числом (p - 1)*(q - 1). Затем вычисляется число d таким образом, что (e*d - 1) делится на (p - 1)*(q – 1).

•e – открытый (public) показатель

•d – частный (private) показатель.

•(n; e) – открытый (public) ключ

•(n; d). – частный (private) ключ.

Делители (факторы) p и q можно либо уничтожить либо сохранить вместе с частным (private) ключом. Если бы существовали эффективные методы разложения на сомножители (факторинга), то, разложив n на сомножители (факторы) p и q, можно было бы получить частный (private) ключ d. Таким образом надежность криптосистемы RSA основана на трудноразрешимой – практически неразрешимой – задаче разложения n на сомножители (то есть на невозможности факторинга n) так как в настоящее время эффективного способа поиска сомножителей не существует.

Шифрование

Предположим, Алиса хочет послать Бобу сообщение M. Алиса создает зашифрованный текст С, возводя сообщение M в степень e и умножая на модуль n: C = M**e* (mod n), где e и n – открытый (public) ключ Боба.

Затем Алиса посылает С (зашифрованный текст) Бобу. Чтобы расшифровать полученный текст, Боб возводит полученный зашифрованный текст C в степень d и умножает на модуль n:

M = c**d*(mod n); зависимость между e и d гарантирует, что Боб вычислит M верно. Так как только Боб знает d, то только он имеет возможность расшифровать полученное сообщение.

Цифровая подпись

Предположим, Алиса хочет послать Бобу сообщение M , причем таким образом, чтобы Боб был уверен, что сообщение не было взломано и что автором сообщения действительно является Алиса. Алиса создает цифровую подпись S возводя M в степень d и умножая на модуль n:

S = M**d*(mod n), где d и n – частный ключ Алисы. Она посылает M и S Бобу.

Чтобы проверить подпись, Боб возводит S в степень e и умножает на модуль n: M = S**e*(mod n), где e и n – открытый (public) ключ Алисы.

Таким образом шифрование и установление подлинности автора сообщения осуществляется без передачи секретных (private) ключей: оба корреспондента используют только открытый (public) ключ своего корреспондента или собственный частный (private) ключ. Послать зашифрованное сообщение и проверить подписанное сообщение может любой, но расшифровать или подписать сообщение может только владелец соответствующего частного (private) ключа.

Скорость работы алгоритма RSA

Как при шифровании и расшифровывании, так и при создании и проверке подписи алгоритм RSA по существу состоит из возведения в степень, которое выполняется как ряд умножений.

В практических приложениях для открытого ключа обычно выбирается относительно небольшой показатель, а зачастую группы пользователей используют один и тот же открытый показатель, но каждый с различным модулем. Если открытый показатель неизменен, то вводятся некоторые ограничения на главные сомножители (факторы) модуля. При этом шифрование данных идет быстрее расшифровывания, а проверка подписи быстрее, чем подписание.

Если k — количество битов в модуле, то в обычно используемых для RSA алгоритмах количество шагов, необходимых для выполнения операции с открытым ключом, пропорционально второй степениk, количество шагов для операций частного ключа — третьей степени k, количество шагов для операции создания ключей — четвертой степени k.

Методы “быстрого умножения” (например, методы, основанные на быстром преобразовании Фурье (Fast Fourier Transform, FFT)) выполняются гораздо меньшим количеством шагов. Тем не менее, они не получили широкого распространения из-за сложности программной реализации, а также потому, что с распространенными размерами ключей они фактически работают медленнее. Однако производительность и эффективность приложений и оборудования, реализующих алгоритм RSA, быстро увеличиваются.

Из изображении явно видна рекурсивная природа алгоритма. Для числа длиной менее четырех разрядов применялось наивное умножение.

Быстрое преобразование Фурье

Будем считать, что наш многочлен имеет степеньn=2k. Если нет, дополним старшие коэффициенты нулями до ближайшей степени двойки.

Основная идея БПФ: Пусть:

A(x)=a0+xa2+x2a4+...+xn/2-1an-2 (четные коэффициэнты P)

B(x)=a1+xa3+x2a5+...+xn/2-1an-1 (нечётные коэффициенты P).

Тогда P(x)=A(x2)+x B(x2).

Теперь применим принцип «разделяй и властвуй»: чтобы посчитать значения P в n точках (ω0,ω1,...), посчитаем значения A и B рекурсивно в n/2 точках (ω0,ω2,...). Теперь значениеP(ωi) восстановить достаточно просто:

P(ωi)=A(ω2i)+ωi B(ω2i)

Если обозначить за ξi=ω2i точки, в которых мы считаем значения многочлена степени n/2, формула преобразится:

P(ωi)=A(ξi)+ωi B(ξi)

Её уже можно загонять в программу, не забыв что i принимает значения от 0 до n-1, а ξi определено лишь от 0 до n/2-1. Вывод — надо будет взять i по модулю n/2.

Время работы выражается рекуррентной формулой T(n)=O(n)+2T(n/2). Это довольно известное соотношение и оно раскрывается в O(n log2n) (грубо говоря, глубина рекурсии — log2n уровней, на каждом уровне суммарно по всем вызовам выполняется O(n) операций).

12. АлгоритмТоома Кука

Исходными данными служат два положительных длинных числа [n, u] и [n, v]; результатом - их произведение [2n, uv]. Используются четыре стека U, V, W и C, в которых при выполнении алгоритма будут храниться длинные числа, и пятый стек, содержащий коды временно приостановленных операций (имеется всего три кода, и для их представления можно воспользоваться малыми целыми числами). Массивы q и г целых чисел имеют индексы от 0 до 10; необходимо выделить память для этих двух массивов и для еще нескольких временных переменных, упомянутых в алгоритме.

1. (Начальная установка.) Сделать все стеки пустыми. Присвоить K значение 1, q0 и q1 - значение 16, r0 и r1 - значение 4, Q - значение 4 и R - значение 2.

2. (Построение таблицы размеров). Пока K < 10 и qK-1 + qK ≥ n, выполнять следующие вычисления. Изменить К на К+1, Q - на Q + R; если (R+1)2 ≤ Q, то изменить R на R+1; установить qK равным 2Q и rk равным 2R. Если цикл оканчивается из-за K = 10, то остановиться, выдав сообщение об ошибке - число битов n слишком велико, массивы q и г переполнились. В противном случае присвоить k значение K. Поместить [qK + qK-1, v] и за ним [qK + qK-1, n] в стек C (вероятно, потребуется добавить к [n, u] и [n, v] слева нули). Поместить в управляющий стек код стоп.

3. (Главный внешний цикл.) Пока управляющий стек не пуст, выполнять шаги с 4-го по 18-й. Если на этом шаге управляющий стек окажется пустым, то остановиться с сообщением об ошибке; в управляющем стеке должен быть по крайней мере один элемент.

4. (Внутренний цикл разбиения u и v.) Пока k > 1, выполнять шаги с 5-го по 8-й,

5. (Установка параметров разбиения.) Установить k равным k - 1, s равным qk, t равным rk и p равным qk-

1 + qk.

6. (Разбиение верхнего элемента стека C.) Длинное число [qk + qk+1, u] на вершине C следует рассматривать

как t + 1 чисел длиной s битов каждое. Разбить [qk + qk+1, u] на длинные числа [s, Ut], [s, Ut-1], ..., [s, U1], [s, U0]. Эти t + 1 чисел являются коэффициентами многочлена степени t, который следует вычислить в

точках 0, 1, ..., 2t - l, 2t no правилу Горнера. Для i = 0, 1, ..., 2t - l, 2t вычислить [p, Xi] по формуле

(...([s, Ut]·i + ... + [s, U1]·i + [s, U0]

и сразу поместить [p, Xi] в стек U. Для выполнения умножений можно использовать подпрограмму умножения длинных чисел на короткие; никакой промежуточный или окончательный результат не потребует более p битов. Удалить [qk+qk-1, u] из стека C.

7. (Продолжение разбиения.) Выполнить над числом [m, v], находящимся сейчас на вершине стека C, ту же последовательность действий, что на шаге 6; полученные числа [p, Y0], ...,[p, Y2t] поместить в стек V в порядке получения. Не забудьте удалить вершину стека C.

8. (Заполнение заново стека C.) Попеременно удалять 2t раз) вершины стеков V и U и помещать эти значения в стек C. В результате значения, вычисленные на шагах 6 и 7, будут помещены, чередуясь, в стек C в обратном порядке. После выполнения этого перемешивания верхняя часть стека C, рассматриваемая снизу вверх, будет иметь вид

[p, Y2t], [p, X2t], ..., [p, Y0], [p, X0],

на вершине будет [p, X0]. Поместить в управляющий стек один код операции интерполировать и 2t кодов операции сохранять и вернуться к шагу 4.

9.(Подготовка к интерполяции.) Присвоить k значение 0. Выбрать два верхних элемента стека C и поместить их в обычные переменные u и v. Оба числа u и v будут состоять из 32 битов. Используя некоторую другую подпрограмму умножения, вычислить [64, w] = [64, uv]. Это умножение можно выполнить аппаратно или с помощью подпрограммы, как вы найдете нужным.

10.(Интерполяция при необходимости.) Выбрать вершину управляющего стека в переменную A. Если значение A есть интерполировать, то выполнить шаги с 11-го по 16-й, в противном случае перейти к

шагу 17.

11. (Организация интерполяции.) Поместить [m, w] в стек W (это может быть значение, полученное на шаге 9 или 16). Присвоить s значение qk, t - значение rk, р - значение qk-i + qk. Обозначим верхнюю часть стека W, рассматриваемую снизу вверх, как

[2р, Z0], [2p, Z1], ..., [2р, Z2t-1], [2p, Z2t],

последнее из этих значений - на вершине стека.

12.(Внешний цикл деления Z.) Выполнять шаг 13 для i = 1, 2, 2t.

13.(Внутренний цикл деления Z.) Присвоить [2p, Zj] значение ([2p, Zj] - [2p, Zj-1])/i для j =2t, 2t - 1, ..., i + 1, i. Все разности будут положительными, а все деления выполняются нацело, т. е. без остатка.

14.(Внешний цикл умножения Z.) Выполнять шаг 15 для i = 2t-1, 2t-2, ..., 2, 1.

15.(Внутренний цикл умножения Z.) Заменить [2р, Zj] на [2р, Zj] - i·[2р, Zj+1] для j = i, i+1, ..., 2t-2, 2t-1. Все разности будут положительными, и все результаты поместятся в 2p битов.

16.(Образование нового w и начало нового цикла.) Присвоить значение многочлена

(... ([2р, Z2t]·2s + [2р, Z2t-1])·2s + ... + [2р, Z1])·2s + [2р, Z0]

переменной [2(qk + qk+1), w]. Этот шаг можно выполнять, используя только сдвиги и сложения длинных чисел. Заметьте, что используется та же переменная [m, w], что и на шаге 9. Удалить [2p, Z2t], ..., [2p, Z0] из стека W. Присвоить k значение k + 1 и вернуться к шагу 10.

17.(Проверка окончания.) Если A имеет значение стоп, то в переменной [m, w], уже вычисленной на шаге 9 или 16, находится результат алгоритма. В этом случае окончить работу.

18.(Сохранение значения.) Значением A должен быть код сохранить (если это не так, завершить алгоритм

по ошибке). Присвоить k значение k + 1 и поместить [qk + qk-1, w] в стек W. Это значение w, только что вычисленное на шаге 9 или 16. Теперь вернуться к шагу 3.

13. Алгоритм быстрого деления.

? Что-то как умножение? о_О

14. Тесты простоты. Числа Камайкла

Тест простоты — алгоритм, который по заданному натуральному числу определяет, является ли это число простым. Различают детерминированные и вероятностныетесты.

Тесты Простоты:

-Проверка делением (делить на всё подряд)

-Тест основанный на малой Теореме Ферма.

Если n — простое число, то оно удовлетворяет сравнению для любого a.

Выполнение сравнения является необходимым, но не достаточным признаком

простоты числа. То есть если хотя бы для одного a , то число n составное, в противном случае ничего сказать нельзя, хотя вероятность того, что число является простым увеличивается.

Если для составного числа n выполняется сравнение , то число n называют псевдопростым по базе a. При проверке числа на простоту тестом Ферма выбирают несколько чисел a. Чем

больше количество a, для которых , тем больше вероятность, что число n простое.

- тест Миллера-Рабина

-символ Лежандра

-Символ Якоби

15. Алгоритмы факторизации. Метод Полларда

Задача факторизации - разложение на множители.

ρ - Метод Полларда.

С помощью этого метода было впервые факторизовано число Ферма . Впервые этот алгоритм был

предложен Дж. Поллардом в 1975 г. Суть его заключается в следующем:

1. Выбираем отображение , где - кольцо вычетов по модулю n. В качестве функции обычно берут полиномы

степени ≥2 (например ).

2. Выбираем некоторое число и строим рекурсивную последовательность по следующему принципу

.

3. Для некоторых номеров i и j вычисляем . Если или , то рассматриваем

другую пару . Если , то d – делитель числа n.

Как видим, алгоритм может оказаться довольно громоздким из-за большого количества пар . Эта проблема решаема с помощью некоторых способов выбора номеров i и j. Рассмотрим некоторые из них:

1., т.е.

2.Если j удовлетворяет условию , то берут

Если окажется, что алгоритм не нашел делителя, то можно попробовать другие функции f, например , где с

– некоторая константа.

Сложность этого алгоритма оценивается, как битовых операций. Существует теорема, которая формулируется так: Пусть n – составное число, вероятность того, что метод Полларда

не сможет найти нетривиальный делитель n за времяне превышает величину . ρ - Метод Полларда обычно используется для нахождения небольших делителей числа n.

(P-1)-метод Полларда.

Прежде чем начать рассмотрение этого алгоритма введем определение: будем говорить, что число k является B-степенно-гладким для некоторого B>0, если : m – простое и является делителем числа k,

выполнено условие , где - наибольшее число такое, что

делит k.

Теперь непосредственно сам алгоритм:

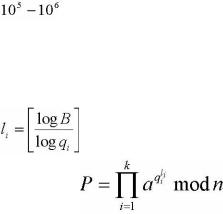
1.Исходя из возможностей нашей вычислительной машины, выбираем границу гладкости B. Обычно B~.

2.Выбираем произвольное целое число a, удовлетворяющее условию , и вычисляем . Если

, то d – искомый делитель.

3.Строим таблицу всех простых чисел и для каждого такого числа находим

,т.е. .

4.Вычисляем

5.Находим . Если , то d – искомый делитель, иначе алгоритм не смог найти делитель. В этом случае можно взять другое основание a или границу гладкости.

Оценка сложности этого метода в худшем случае составляет арифметических операций. Однако в некоторых случаях этот алгоритм может довольно быстро найти делитель n.

16. Система Мак-Элиса

_________________________________1

__________________________________2

17-18. Задачадекодирования линейных кодов - труднорешаемая задача

19. Атака на систему Мак-Элиса