1.4Условная плотность распределения вероятностей

1.4.1.Формулы Байеса. Условные математическое ожидание и матрица ковариаций

1.4.2 Правила нахождения параметров условной гауссовской плотности

1.4.3 Примеры нахождения параметров условной гауссовской плотности

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет аэрокосмического приборостроения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Glava1-TV.pdf

Скачиваний:

117

Добавлен:

02.04.2015

Размер:

1.29 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2116 17 18 19 20 21 > Следующая >>>

Внастоящем разделе вводится имеющее существенное значение в теории оценивания понятие условной (апостериорной) ф.п.р.в. и рассматривается правило вычисления параметров условной гауссовской плотности двух векторов, при условии, что один из них зафиксирован. Обсуждается весьма важный при решении задач оценивания пример нахождения параметров условной гауссовской плотности, а также задача регрессии, имеющая тесную связь с байесовскими задачами оценивания, которые рассматриваются в главе 2.

Пусть заданы два случайных вектора x и y , для которых будем полагать известной

совместную ф.п.р.в. fx,y (x, y) . Осуществляя интегрирование этой функции по x или y , можем

получить согласно (1.2.5) соответственно ф.п.р.в. fy ( y) и f x (x) , определяющие

статистические свойства для каждого вектора по отдельности. При независимости векторовx и y

fx,y (x, y) = fx (x) fy ( y) .

В более общем случае справедлива формула умножения плотностей вероятности, которая

записывается как
fx,y (x, y) = f	(x / y) fy ( y) = f ( y / x) fx (x).		(1.4.1)
Входящие в эти соотношения плотности	f (x / y)	и f ( y / x) определяют статистические
свойства векторов x и y при условии, что вектор,		стоящий справа от черты фиксирован.

Поэтому эти плотности называются условными плотностями распределения вероятности или просто условными плотностями. При решении задач оценивания условные плотности f (x / y) и f ( y / x) также называют апостериорными плотностями, тем самым

подчеркивается тот факт, что эти плотности соответствуют апостериорной ситуации, т.е. такой, при которой один из векторов, связанный с оцениваемым вектором, фиксируется. В этом

случае исходные плотности f x (x) , fy ( y)		принято называть априорными. Из соотношения
(1.4.1) следует, что
f (x / y) =		fx,y (x, y)	=	fx,y (x, y)	,	(1.4.2)
	∫	fx,y (x, y)dx		fy ( y)

Соотношения (1.4.2), (1.4.3) известны как – формулы Байеса. Они обеспечивают возможность нахождения условных плотностей по известной совместной плотности fx,y (x, y) .

Из них, в частности, следует, что при независимости векторов x и y условные и априорные ф.п.р.в. между собой совпадают.

Согласно (1.4.2) условную плотность формально можно получить в два приема. Сначала в совместной плотности fx,y (x, y) фиксируется значение y , т.е. fx,y (x, y = y* ) . Относительно x

функция fx,y (x, y = y* ) будет пропорциональна условной плотности, т.е.

fx,y (x, y = y) f (x / y = y ) . Иными словами, условная плотность как функция x				подобна
совместной ф.п.р.в. при	фиксированном значении	y .	Далее для того, чтобы	функция
fx,y (x, y = y* ) приобрела	свойства ф.п.р.в., необходимо,		обеспечить выполнение	условия
нормировки (1.2.4). Для этого функцию fx,y (x, y = y* )		требуется разделить на независящую от

x величину, представляющую собой интеграл от fx,y (x, y = y* ) по аргументу x . Полученная в результате величина совпадет с fy ( y = y* ) , в силу условия согласованности (1.2.5).

Математическое ожидание

xˆ( y) = ∫x f (x / y)dx

и матрица ковариаций

P x / y = ∫(x − xˆ( y))(x − xˆ( y))T f (x / y)dx ,

соответствующие f (x / y) , называют условным математическим ожиданием и условной матрицей ковариаций. В случае, когда речь идет о скалярной с.в., используют понятие

условной дисперсии.

Условные плотности распределения обладают теми же свойствами, что и обычные плотности. В частности, если рассмотреть плотность для трех векторов fx,y,z (x, y, z) , то,

привлекая условие согласованности (1.2.5), можно записать следующие равенства:

f (x / z) = ∫ f (x, y / z)dy;	(1.4.4)
f (x / z) = ∫ f (x / y, z) f ( y / z)dy.	(1.4.5)

Выражения (1.4.4), (1.4.5) удобно использовать в случае необходимости исключения аргументов, стоящих слева и справа от черты в условной плотности [1.7].

Получим соотношения, позволяющие находить параметры условной гауссовской плотности распределения. Предположим, что совместная ф.п.р.в. двух гауссовских векторов

x и y , размерности n и m имеет вид

fx,y (x, y) = N

(x т , y т )т; (x т , y т )т , P

(1.4.6)

где

P x

P xy

P =

P y

(P xy )т

Ясно, что для каждого вектора по отдельности для ф.п.р.в. справедливо представление

f x (x) = N (x; x, P x ),

(1.4.7)

fy ( y) = N (y; y, P y ).

(1.4.8)

Найдем параметры условной плотности распределения вероятности

f (x / y) ,

полагая

фиксированным значение вектора

y .

Предварительно

запишем

выражение

для

обратной

матрицы

P−1

(1.4.9)

В соответствии с правилами обращения блочных матриц можно записать [1.9, с107]

− P

−1

+ (P

x −1

−1

,(1.4.10)

A = P

)

= (P

)

B = −AP xy (P y )−1 = −(P x )−1 P xy C ,

− P

−1

+ (P

−1

C = P

)

= (P

)

Используя (1.4.2) с учетом (1.4.6) и (1.4.8) можем записать

(x т , y т ) ; (x т , y

т )

(P xy )т

P y

f (x / y) =

N ( y; y, P y )

Это выражение нетрудно преобразовать к виду [1.9]

f (x / y) =

exp −

J (x, y)

(2π)n / 2

P y

(1.4.11)

(1.4.12)

(1.4.13)

80
в котором
J (x, y) = [(x − x)T ( y − y)T ] A		B	y	−1	x − x	.
	T	C − (P	y	)
B		C − (P		)	( y − y)

Учитывая (1.4.11), (1.4.12), можем записать

J (x, y) = [(x − x)т , ( y − y)т ] A

−1

(x − x)

C −

)

( y − y)

= (x − x)т A(x − x) + (x − x)т B( y − y) + ( y − y)т B т (x − x) + ( y − y)

т C − (P y )−1 ( y −

= (x − x)т A(x − x) + 2(x − x)т AP xy (P y )−1 ( y − y) + ( y − y)т (P y )−1 P yx AP xy

(P y )−1 ( y

−1

(x − x) − P

)

( y − y)

A (x − x) − P

)

( y − y) .

Отсюда следует, что

J (x, y) = (x − xˆ)т A(x − xˆ) ,

ˆ =

y −1

( y

−

y) .

где x

)

Преобразуем теперь первый сомножитель в (1.4.13). Запишем

y) =

− y) =

(1.4.14)

P x

P xy

−1

P =

= P

−

)

−1

(P xy )т

P y

(P y )

P yx

Отсюда с очевидностью получаем

и таким образом

P x − P xy (P y )−1 P yx

P y

− P xy (P y )−1 P yx

P x

(1.4.15)

P y

f (x / y) является

Анализ соотношений (1.4.13)-(1.4.15) показывает, что условная плотность

гауссовской, т.е. f (x / y)

x / y

ее

параметры

определяются

с помощью

N (x; x( y), P

следующих соотношений

−1

( y

−

y) ,

(1.4.16)

x( y)

)

P x / y

= P x

− P xy (P y )−1 (P xy )т .

(1.4.17)

Соотношения (1.4.16), (1.4.17) определяют правило нахождения параметров условной гауссовской плотности для двух совместно гауссовских векторов.

f ( y / x) =

fx,y (x, y)

fx,y (x, y)

fx,y (x, y)dy

Конкретизируем полученные в предыдущем подразделе выражения для двух примеров. Пример 1.4.1. Пусть задан двумерный центрированный гауссовский случайный вектор

x = (x1 , x2 )т с матрицей ковариаций вида (1.2.14). Требуется найти параметры условной гауссовской плотности для первой его компоненты в предположении, что вторая компонента зафиксирована.

С учетом (1.2.14), (1.2.15), (14.16), (1.4.17) можно записать следующие соотношения для условного математического ожидания и условной дисперсии

	xˆ = r		σ1			x			,
	xˆ = r					x			,
	1		σ		2		2
					2
	σ12усл	=σ12 (1− r 2 ) ,
т.е.
											1				1					σ1			2
														exp −										.
	f (x	/ x		2	)	=												x	− r		x	2
	f (x	/ x			)	=						2				2	2	x	− r		x
	1							σ			2π(1 − r	2	)		2(1 − r	2	2	1		σ2
								σ		1	2π(1 − r		)		2(1 − r		)σ1			σ2
										1
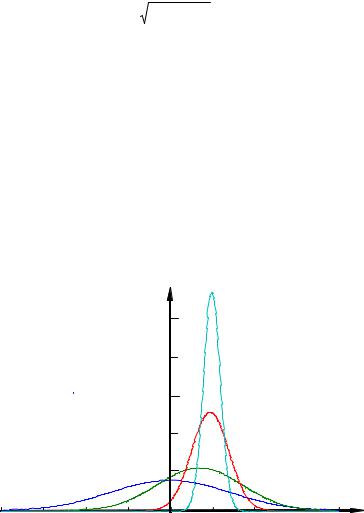
На Рис. 1.4.1	представлены графики условных плотностей приσ1 = σ2 =1																		при различных
значениях r и	x2 =1 . Из графиков следует,										что при увеличении коэффициента корреляции

условная дисперсия уменьшается. Это вполне закономерно, поскольку коэффициент корреляции отражает степень статистической зависимости одной величины относительно другой. Чем больше эта зависимость, тем существеннее уменьшается условная дисперсия по

						σ1
	f (x	/ x			x −	σ1	x
сравнению с априорной. Нетрудно заметить, что при r →1 ,			2	) → δ				2	.
сравнению с априорной. Нетрудно заметить, что при r →1 ,				) → δ					.
	1				1	σ2
						σ2

f(x1/ x2)

2.5	r=0.99

1.5

				1		r=0.95
						r=0.95
				0.5		r=0.7
		r=0				r=0.7
		r=0
0	-3	-2	-1	0	1	2	3	4
-4	-3	-2	-1	0	1	2	3	4	x1
									x1

Рис.1.4.1 Графики гауссовской условной плотности распределения при различных значениях нормированного коэффициента корреляции. ♦

Пример 1.4.2. Пусть так же, как и в примере 1.3.5, для двух векторов x и v размерности n и m определены математическое ожидание и матрица ковариаций, и, кроме того, известно, что их совместное распределение гауссовское, т.е.

	x x		x	B		(1.4.18)
fx,v (x, v) = N	; , P			B	.	(1.4.18)
	v v	BT		Pv

Пусть вектор y связан с x и v соотношением вида
y = Hx + v .						(1.4.19)

Необходимо найти условную плотность распределения вероятности f (x / y) .

В решении этой задачи удобно выделить два этапа.

Суть первого этапа сводится к нахождению плотности распределения вероятности совместного вектора, включающего x и y . В разделе 1.3.3 (пример 1.3.5) было показано, что

+ B

.(1.4.20)

fx,y (x, y) = N

;

y Hx + v B т + HP x

HP x H т +

HB + B тH т + Pv

Искомую плотность f (x / y) легко получить на втором этапе, используя приведенное выше

правило нахождения условной гассовской плотности. Применяя это правило, получаем, что

f (x / y)	=	ˆ	x / y	),	(1.4.21)
		N(x; x( y), P

где условное математическое ожидание и условная матрица ковариаций в соответствии с выражениями (1.4.16), (1.4.17) определяются как

xˆ( y) = x + (P x H т + B)(HP x H т + HB + B тH т + Pv )−1( y − Hx − v) ,	(1.4.22)
P x / y = P x − (P x H т + B)(HP x H т + HB + B тH т + Pv )−1 (B т + HP x ) .	(1.4.23)

В частном случае, когда векторы x и v независимы и v = 0 , эти выражения упрощаются

xˆ( y) = x + K ( y − Hx) ,	(1.4.24)
K = P x H т(HP x H т + Pv )−1 ,	(1.4.25)
P x / y = P x − P x H т(HP x H т + Pv )−1 HP x .	(1.4.26)

Для вычисления условной матрицы ковариаций может быть также использовано

соотношение
	−1		−1
P x / y = P x − P x H т(HP x H т + Pv )−1 HP x =	(P x )	+ H т(Pv )−1 H	, (1.4.27)

в справедливости которого легко убедиться с помощью леммы об обращении матриц. Принимая во внимание соотношение (1.4.27) и очевидную цепочку равенств [1.9]

P x H т (HP x H т + Pv )−1 = [(P x )−1 + H т (Pv )−1 H ]−1 [(P x )−1 + H т (Pv )−1 H ]P x H т (HP x H т + Pv )−1 =
= P x / y [H т + H т (Pv )−1 HP x H т ](HP x H т + Pv )−1 = P x / y H т (Pv )−1 ,
для матрицы K в (1.4.25) получаем следующее выражение
	K = P x / y H т (P v )−1 .♦								(1.4.28)
По аналогии с результатом, полученным в примере для							f (x / y) , можно показать, что (см.
задачу 1.4.2)						),
	f ( y / x)	=		ˆ	y / x				(1.4.29)
	f ( y / x)		N (y; y(x), P						(1.4.29)
где
	yˆ(x) = Hx + v + B т(P x )−1(x − x) ,								(1.4.30)
	P y / x = Pv − B т (P x )−1 B .								(1.4.31)
Нетрудно заметить, что	vˆ(x) = v + Bт (P x )−1(x − x)				и		P y / x = P v / x		представляют собой
условное математическое ожидание и матрицу ковариаций вектора								v	при фиксированном
значения вектора x . Это	вполне объяснимо,			поскольку			y = Hx + v ,		и при фиксации x
математическое ожидание и матрица ковариаций случайного вектора								y	будут определяться
условным математическим ожиданием и условной матрицей ковариаций вектора v .
Наиболее важные выражения, связанные с задачей нахождения								параметров условной

гауссовской плотности широко и часто используемые при решении задач оценивания, сведены в таблицу 1.4.1.

Таблица 1.4.1.

Нахождение параметров условной гауссовской плотности

Условия

Задача

Решение

Найти

)

Задана ф.п.р.в.

условную

f (x / y)

x /

x ;

x ,

ф.п.р.в.

(x; x( y), P

x, y

(x, y) = N

f (x / y)

xy y

−1

−

P y

)

( y

(P xy )т

для

x( y)

x / y

= P

− P

)

−1

)

вектора

Найти

f (x / y)

x / y

условную

N (x; x( y), P ),

Задана ф.п.р.в.

xˆ( y) = x + K ( y

− Hx) ,

ф.п.р.в.

K = P x H т(HP x H

т + Pv )−1 ,

x x

f (x / y)

fx,v (x,v) = N

;

, P

P x / y = P x − P x H т (HP x H т + Pv )−1 HP x ,

v 0

−1

и вектор

−1

+ H т

y = Hx + v

P x / y = (P x )

(Pv )−1 H ,

K = P x / y H т (Pv )−1 .

Найти

условную ф.п.р.в. f ( y / x)

f ( y / x) = N(x; yˆ(x), P y / x ),

yˆ(x) = Hx + v + (B т + HP x )(P x )−1(x − x) ,

P y / x = Pv − B т (P x )−1 B .

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2116 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.04.201550.52 Кб14Finansy_kursach_2.docx
#
14.03.201649.74 Кб21Fizika laba.docx
#
02.04.2015154.62 Кб3FLOID.doc
#
14.03.2016595.46 Кб15Fotometr_Metodicheskie_ukazania_k_vypolneniyu_laboratornykh_rabot.doc
#
02.04.2015291.33 Кб27Fuck Them ALL.doc
#
02.04.20151.29 Mб117Glava1-TV.pdf
#
02.04.20154.03 Mб17GrushoCrypto.pdf
#
02.04.201529.25 Кб23GUAP (1).docx
#
02.04.201554.79 Кб108GUAP_Laboratornaya_rabota_14.docx
#
14.03.20165.6 Mб25haritonov.pdf
#
02.04.2015634.37 Кб12HTML.doc