7. Паутинообразная модель

Паутинообразная модель разработана голландским экономи­стом Я. Тинбергеном на основе анализа экономического цикла в свиноводстве (1930г.) и считается одним из первых эконометриче­ских исследований экономического цикла. В данной модели ис­пользуется принцип сжатых отображений. Этот принцип сформу­лирован в виде теоремы, утверждающей существование и единст­венность неподвижной точки множества при некотором специаль­ном («сжимающем ») отображении множества в себя, т.е. . В зависимости от свойств множестваи отображенияформули­руются и доказываются различные теоремы о неподвижной точке. Эти теоремы представляют эффективное средство анализа в совре­менной математике, включая экономико-математическое модели­рование. Точка (элемент)множестваназывается неподвижной точкой отображения, если. При анализе экономико-мате­матических моделей используются теоремы о неподвижной точке, принадлежащие голландскому математику Л. Бауэру и японскому математику Ш. Какутани.

Теорема Брауэра. Пусть:

• - непустое замкнутое выпуклое ограниченное множе­ство в пространстве ;

• - векторная функция, определенная на множестве 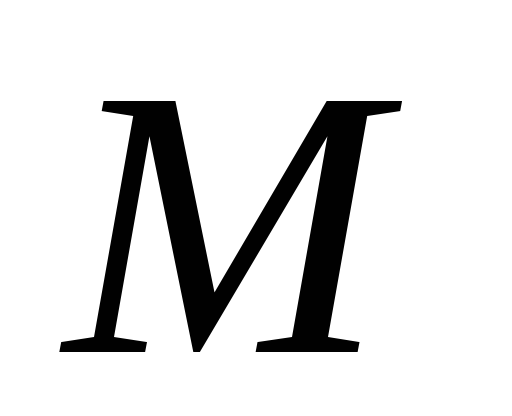и отображающая;

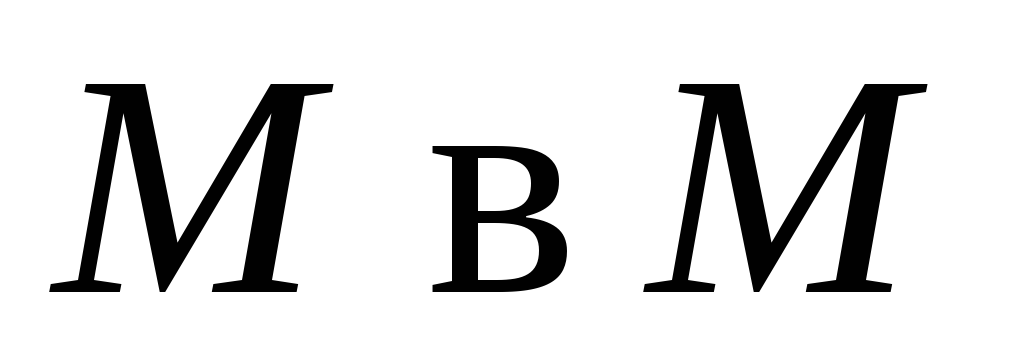• функция 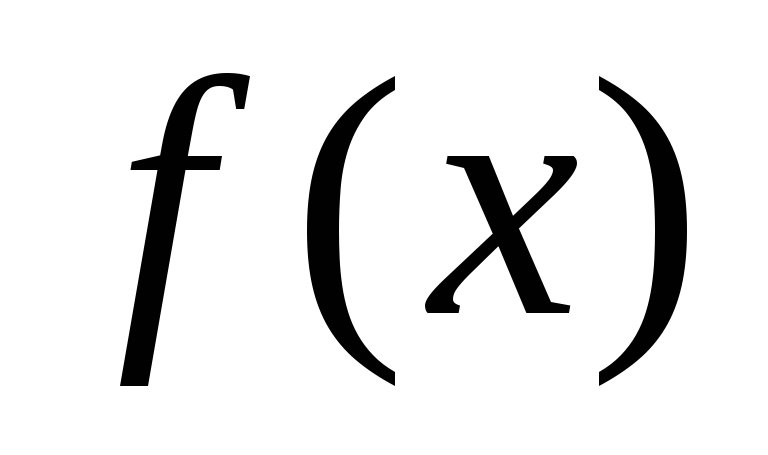непрерывна на множестве.

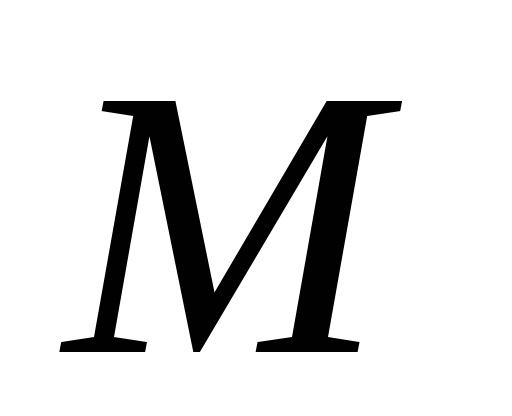Тогда функция имеет неподвижную точку, т.е., или в координатной форме

.

Теорема Какутани. Пусть - непустое замкнутое выпуклое ограниченное множество в пространстве, пусть- точечно-множественное отображение, удовлетво­ряющее условиям:

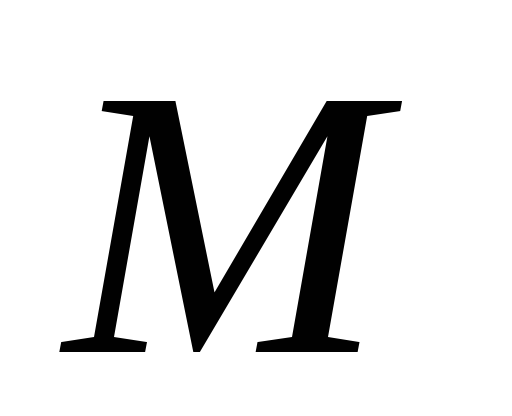• для каждой точки из множествасоответствующее множе­ствоявляется непустым выпуклым подмножест­вом множества;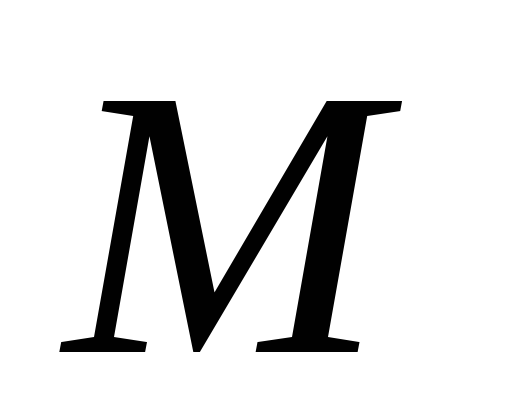

• отображение замкнуто.

Тогда отображение имеет неподвижную точку, т.е..

Примечание: Отображение называется точечно-множественным (или многозначным), если оно ставит в соот­ветствие каждому элементуиз множестваодно вполне определенное (непустое) подмножествомножества, что записывается так:.

Для того чтобы сформулировать еще одну теорему о непод­вижной точке, приведем важное определение. Отображение метрического пространствав себя называется сжимаю­щим, если существует такое число, что для любых точек (элементов)ииз множествасправедливо неравенство

,

где исоответственно расстояния между точкамии, и их образами.

Теорема о неподвижной точке сжимающего отображения. Пусть - полное метрическое пространство¹, а - сжимающее ото­бражение. Тогда отображениеимеет единственную неподвиж­ную точку, т.е.. Для любой точкипоследо­вательность

(7.1.)

сходится к неподвижной точке . При этом справедлива оценка погрешности

.

Элементы последовательности (7.1.) называются последователь­ными приближениями неподвижной точки . Нахождение точкис помощью последовательных приближений (7.1.) есть частная версия общего метода² последовательных приближений.

Теорема о неподвижной точке сжимающего отображения по­зволяет доказать теоремы существования и единственности реше­ния дифференциальных, интегральных и других уравнений, систем алгебраических уравнений (так называемого балансового) вида . Искомые решения могут быть найдены с любой наперед заданной степенью точности с помощью конечного числа первых членов последовательности (7.1.). Это число первых членов по­следовательности (7.1.) зависит от точности, с которой требуется найти решение. В частности, если сумма модулей элементов каж­дого столбца квадратной матрицыстрого меньше единицы, то из теоремы о неподвижной точке для сжимающего отображения следует, что системаимеет единственное решение при лю­бом векторе.

Таким образом, принцип сжимающих отображений утвер­ждает существование и единственность неподвижной точки мно­жества при некотором специальном (т.е. «сжимающем») отображе­нии множества в себя. Произвольное отображение метрического пространствав себя, которое каждой точкеиз, порождает в пространствеуравнение

. (*)

Действие отображения на точкуможно интерпретировать как перемещение ее точку. Точканазывается неподвижной точ­кой отображения, если выполняется равенство (*). Таким обра­зом, вопрос о разрешимости уравнения (*) является вопросом о на­хождении неподвижных точек отображения.

Отображение метрического пространствав себя называ­ется сжимающим, если существует такое положительное число, что для любых точекиизвыполняется неравенство

,

где - расстояние между точкамииметрического простран­ства.

Принцип сжимающих отображений утверждает, что каждое сжимающее отображение полного метрического пространства в себя имеет, и притом только одну, неподвижную точку. Кроме того, для любой начальной точки из пространствапоследователь­ные приближения, определяемые рекуррентными соотноше­ниями. При этом справедлива следующая оценка по­грешности:

.

Таким образом, в условиях применимости принципа сжи­мающих отображений решение может быть с наперед заданной точностью вычислено с помощью метода последовательных при­ближений.

С помощью определенного выбора полного метрического пространства и построения отображенияэти задачи сводят предварительно к уравнению (*), а затем находят условия, при ко­торых отображение оказывается сжимающим.

Рассмотрим следующую задачу. Пусть рынок какого-либо от­дельного товара характеризуется следующими функциями спроса и предложения:

.

Для существования равновесия цена должна быть такой, чтобы товар на рынке был распродан, т.е.

.

Динамическая модель получается при наличии запаздывания спроса или предложения. Простейшая модель с дискретным време­нем предполагает неизменное запаздывание предложения на один интервал времени:

.

Паутинообразная модель может быть описана следующим об­разом: объем предложения на рынке в текущий момент времени является функцией цены, действовавшей в предшествующий мо­мент времени. Ценав текущий момент временидолжна уста­новиться таким образом, чтобы был куплен весь объем пред­ложенного товара. Иными словами, ценаи объем покупок – про­дажхарактеризуется уравнением:

.

Решение можно проиллюстрировать диаграммой, представ­ленной на рис. 7.1., где и- соответственно кривые спроса и предложения, а положение равновесия (со значениямии) соот­ветствуют точке пересечения. В начальный момент временина рынке действует цена. Она определяет в соответствии с кривой предложения количество товара, которое будет находиться на рынке в момент времени. Это количество товара может быть рас­продано в соответствии с кривой спроса по цене. Цена, в свою очередь, определить размер предложенияв момент времени. Продолжение этого процесса и дает график паутины, показанный на рис. 7.1. При «развороте» паутины во времени (рис. 7.2.,7.3.) видно, что цены и объемы покупок-продаж совершают зату­хающие колебания и стремятся к уровням равновесия.

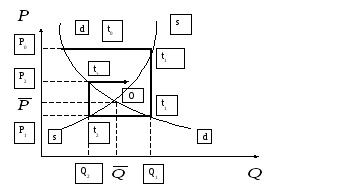
Рис. 7.1.График паутины с затухающими колебаниями

Можно утверждать, что движение с затухающими колеба­ниями возникает, если кривая имеет меньшую крутизну, чем кри­вая. Взрывное колебательное движение возникает в том слу­чае, когда криваяимеет большую крутизну, чем кривая(рис. 7.4.). При равных углах наклона кривыхивозникают регуляр­ные колебания, т.е. незатухающие и невзрывные (рис. 7.5.). Для случая линейных функций спроса и предложения реше­ние может быть получено алгебраически.

Рис. 7.2. «Разворот» динамики цен во времени

Рис. 7.3. «Разворот» динамики объемов закупок-продаж во времени

Рис. 7.4. График паутины со взрывными колебаниями

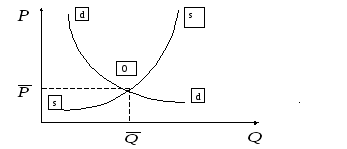
Рис. 7.5. График паутины с регулярными колебаниями

В паутинообразной модели случай с продолжающимися и правильными колебаниями крайне редок. Интересен случай с зату­хающими колебаниями. Существует его развитие, которое позво­ляет представить движение с продолжающимися колебаниями во времени. Для этого вместо кривых спроса и предложения, неиз­менных во времени, можно взять кривые, которые под воздейст­вием внешних сил изменяются во времени либо регулярно, либо циклично, либо как-нибудь иначе. Тогда еще до прекращения коле­баний, показанных на рис. 7.2., 7.3. сдвиг кривыхилипри­ведет к возмущению, и колебания появятся снова.