
- •ПРЕДИСЛОВИЕ
- •ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
- •1. КОМБИНАТОРИКА
- •2. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
- •2.1. Классическое определение вероятности
- •2.2. Геометрические вероятности
- •2.3. Теоремы сложения и умножения вероятностей
- •2.4. Формула полной вероятности
- •2.5. Формулы Байеса
- •2.6. Повторные независимые испытания
- •2.6.1. Формула Бернулли
- •2.6.2. Обобщенная формула Бернулли
- •2.7. Простейший (пуассоновский) поток событий
- •2.8. Случайные величины. Функция распределения. Функция плотности вероятности. Числовые характеристики
- •2.8.1. Случайные величины
- •2.8.2. Функция распределения
- •2.8.3. Функция плотности вероятности
- •2.8.4. Числовые характеристики случайных величин
- •2.9. Нормальный закон распределения
- •2.10. Асимптотика схемы независимых испытаний
- •2.10.2. Формула Пуассона
- •2.11. Функции случайных величин
- •2.12. Функции нескольких случайных аргументов
- •2.12.1. Свертка
- •2.12.2. Распределение системы двух дискретных случайных величин
- •2.12.3. Распределение функции двух случайных величин
- •2.13. Центральная предельная теорема
- •2.14. Ковариация
- •2.14.1. Корреляционная зависимость
- •2.14.2. Линейная корреляция
- •2.15. Функциональные преобразования двухмерных случайных величин
- •2.16. Правило «трех сигм»
- •2.17. Производящие функции. Преобразование Лапласа. Характеристические функции
- •2.17.1. Производящие функции
- •2.17.2. Преобразование Лапласа
- •2.17.3. Характеристические функции
- •3. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- •3.1. Точечные оценки
- •3.1.1. Свойства оценок
- •3.1.2. Оценки для математического ожидания и дисперсии
- •3.1.3. Метод наибольшего правдоподобия для оценки параметров распределений
- •3.1.4. Метод моментов
- •3.2. Доверительный интервал для вероятности события
- •3.3. Проверка гипотезы о равенстве вероятностей
- •3.4. Доверительный интервал для математического ожидания
- •3.4.1. Случай большой выборки
- •3.4.2. Случай малой выборки
- •3.5. Доверительный интервал для дисперсии
- •3.6. Проверка статистических гипотез
- •3.6.1. Основные понятия
- •3.6.2. Критерий согласия «хи-квадрат»
- •3.6.3. Проверка гипотезы о независимости двух случайных величин
- •3.6.4. Проверка параметрических гипотез
- •3.6.5. Проверка гипотезы о значении медианы
- •3.6.6. Проверка гипотезы о равенстве математических ожиданий
- •3.7. Регрессионный анализ. Оценки по методу наименьших квадратов
- •3.8. Статистические решающие функции
- •4. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- •4.1 Стационарные случайные процессы
- •4.2. Преобразование случайных процессов динамическими системами
- •4.3. Процессы «гибели и рождения»
- •4.4. Метод фаз Эрланга
- •4.5. Марковские процессы с дискретным множеством состояний. Цепи Маркова
- •4.6. Марковские процессы с непрерывным временем и дискретным множеством состояний
- •4.7. Модели управления запасами
- •4.8. Полумарковские процессы
- •5. НЕКОТОРЫЕ ИНТЕРЕСНЫЕ ЗАДАЧИ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ПРИЛОЖЕНИЯ
- •ОГЛАВЛЕНИЕ

n |
|
|
|
|
|
если сумма åxi |
окажется меньше величиныnm0 – 1,65s |
n |
, то гипотезу |
||
i=1 |
|
|
|
|
|
Н0 следует отвергнуть в пользу альтернативной гипотезы Н1. |
|||||
Ответ. W0 |
ì n |
|
ü |
||
|
|||||
= íåxi < nm0 – 1,65s |
n ý. |
||||
|
î i=1 |
|
þ |
||
Задача 3.21. Физическая величина a измеряется прибором, средний квадрат ошибки которого равенs2. Получены результаты n независимых
измерений X1 , X 2 ,K, X n . Здесь X i |
= a + Yi , где Yi –– ошибка прибора при i- |
|
|||||||||||||||
м измерении. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Полагая, |
что |
ошибки |
|
измерений |
имеют |
нормальный |
закон |
||||||||
распределения |
N (0;s2 ), |
постройте |
наиболее мощный |
критерий |
для |
||||||||||||
проверки |
гипотезы H0 : |
a = a0 |
против |
|
|
альтернативы: |
для |
нечетных |
|||||||||
вариантов H1 : |
a = a1 < a0 ; для четных вариантов H1 : |
a = a1 > a0 . |
|
||||||||||||||
|
|
Вероятность ошибки первого рода возьмите равной 0,02. |
|
|
|||||||||||||
|
|
У к а з а н и е . Так как M ( X i ) = M (a + Yi =) |
M (a) + M=(Yi ) |
a + 0 = a, а |
|
||||||||||||
D( X |
) = D(a |
+ Y= ) D(a) + =D(Y ) 0 + s2 , то |
X |
i |
~ N (a;s2 ). |
|
|
|
|
||||||||
|
i |
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
(См. пример 3.21, a –– номер |
варианта, |
n равно номеру варианта |
|||||||||||||
плюс 50). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3.6.5. Проверка гипотезы о значении медианы |
|
|
|
||||||||||
|
|
Пусть Х непрерывная случайная величина, а m –– значение ее медианы, |
|
||||||||||||||
т.е. |
Р( Х £ m) = P( X ³ m) =1 / 2. Проделано n независимых наблюдений над |
||||||||||||||||
случайной величиной. Можно ли считать по их результатамХ1 , Х 2 ,¼, Х n , |
|
||||||||||||||||
что |
|
значение |
медианы |
равноm0 |
|
против альтернативы, что значение |
|||||||||||
медианы равно m1 (для определенности пусть m1 < m0 )? |
|
|
|
|
|||||||||||||
|
|
Предположим, |
что |
значение m действительно равноm0 |
(т.е. верна |
|
|||||||||||
нулевая гипотеза Н0 : |
m = m0 ) и рассмотрим последовательность величин |
|
|||||||||||||||
|
|
|
|
|
Х1 - m0 , Х 2 - m0 ,¼, Х n – m0. |
|
|
|
|
||||||||
|
|
Если |
|
гипотеза |
верна, то |
|
Р( Х – m0 ³ 0) = Р( Х – m0 £ 0) =1 / 2. |
|
|||||||||
Подсчитаем |
число положительных |
|
разностейХ – m0 в |
нашей выборке |
и |
||||||||||||
обозначим его через S. |
|
|
|
|
|
|
|
n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величину S можно представить в виде S = åI ( X i |
- m0 ) , |
где I (x) =1 |
|
||||||||||||
|
|
х > 0 и |
I (x) = 0 |
при х < 0 . |
|
|
|
|
|
|
i=1 |
|
величина I (x) |
|
|||
при |
|
Заметим, |
что |
случайная |
|
||||||||||||
принимает |
два |
значения0 и 1 |
с |
вероятностями р =1 / 2 |
каждое, если |
|
|||||||||||
229

гипотеза верна. Поэтому при верной нулевой гипотезе величинаS имеет биномиальное распределение:
Р(S = k) |
C |
k æ 1 |
ök |
æ |
1 ön-k |
||
n ç |
|
÷ |
ç |
|
= |
||
|
|
||||||
|
|
2 |
2 |
÷ |
|||
|
|
è |
ø |
è |
ø |
||
n
Cnk æç 1 ö÷ . = è 2 ø
Очевидно, что при медиане равной m1 < m0 вероятность Р( Х > m0 ) = = p1 <1 / 2.В итоге задача сводится к проверке гипотезыН0 : р = р0 =1 / 2 против альтернативы Н1 : р = р1 <1 / 2.
Согласно лемме Неймана––Пирсона для любого 0 < a <1 существует такая постоянная величина С > 0 , что значения k, для которых
Сk pk (1 |
- p )n-k |
³C |
|
n |
1 |
1 |
|
Ck |
pk (1 |
- p )n-k |
|
n |
0 |
0 |
|
образуют критическую область наиболее мощного критерия. Так же как и в примере 3.19 легко показать, что в критическую область следует относить в первую очередь самые маленькие значенияk. Остается только найти
k
наибольшее k, для которого åCnk (1 / 2)n £ a , где a –– вероятность ошибки
i=1
первого рода.
Пример 3.22. По результатам независимых наблюдений случайной
величины |
Х1 = 3,05; |
Х 2 = 2,9; |
Х 3 = 3,4; Х 4 = 2,3; |
Х 5 = 4,7; |
Х 6 = 3, 27; |
||
Х 7 = 2,35; |
Х8 =1,54; |
Х 9 = 4,1; |
Х10 = 2,8; Х11 = 3,9; |
Х12 =1,8 исследователь |
|||
в отношении медианыm отверг гипотезуН0 : |
m = m0 = 3,5 |
и |
принял |
||||
альтернативную гипотезу Н1 : |
m = m1 < 3,5. Какова |
вероятность |
ошибки |
||||
первого рода при таком выводе?
Решение. Ошибка первого рода совершается, когда отвергается верная гипотеза. Предположим, что нулевая гипотеза верна и медианаm действительно равна 3,5. Только в трех наблюдениях результаты превосходят 3,5. Как было показано выше, при альтернативе m = m1 < 3,5 в критическую область следует включать в первую очередь малые значения
k. Значение k = 3 было отнесено исследователем к критической области. В предположении, что гипотеза верна имеем
Р (0) |
= С |
0 |
æ 1 |
ö12 |
= |
1 |
; |
=Р (1) |
С1=æ |
1 |
|
ö12 |
12 |
; |
|||||||
|
ç |
|
÷ |
|
|
|
÷ |
|
|
||||||||||||
12 |
12 |
2 |
|
4096 |
|
|
12 |
12 |
ç |
2 |
|
4096 |
|
|
|||||||
|
|
|
è |
ø |
|
|
|
|
|
è |
|
ø |
|
|
|||||||
|
|
2 |
æ 1 |
ö12 |
|
66 |
|
|
|
3 |
æ 1 |
ö12 |
220 |
|
|
||||||
Р (2) |
= С |
|
|
|
|
|
= |
|
|
; |
=Р (3) |
С= |
|
|
|
|
|
|
|
|
. |
|
ç |
|
÷ |
|
|
ç |
|
|
|
÷ |
|
|
|
||||||||
12 |
12 |
|
|
4096 |
|
|
12 |
12 |
|
|
|
4096 |
|
||||||||
|
|
|
è |
2 ø |
|
|
|
|
|
è |
2 ø |
|
|||||||||
230
3 |
æ 1 |
12 |
|
299 |
|
|
|||
ö |
|
|
|
||||||
k |
|
|
|
||||||
Откуда åC12 |
ç |
|
|
÷ |
= |
|
|
» 0,07. |
|
2 |
4096 |
|
|||||||
k =0 |
è |
ø |
|
|
|
||||
Ответ. |
|
|
299 |
» 0,07. |
|
||||
4096 |
|
||||||||
|
|
|
|
|
|||||
Задача 3.22. По результатам независимых наблюдений случайной |
|||||||||
величины Х1, |
|
|
Х 2 , |
Х 3 , Х 4 , |
Х 5 , Х 6 , Х 7 , Х8 , Х 9 , Х10 , Х11 , Х12 |
||||
исследователь в отношении медианыm отверг гипотезу Н0 : m = m0 = 3,5 и принял альтернативную гипотезу Н1 : m = m1 < 3,5. Какова вероятность ошибки первого рода при таком выводе? (См. пример 3.22 и исходные данные.)
Исходные данные к задаче 3.22.
№ |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
X11 |
X12 |
med |
1 |
1,3 |
–0,1 |
0,3 |
–0,9 |
1,9 |
1,1 |
0,8 |
2,1 |
1,5 |
1,2 |
2,0 |
1,4 |
1,6 |
2 |
0,7 |
2,1 |
–0,2 |
1,9 |
–0,4 |
2,4 |
1,8 |
1,9 |
–0,3 |
0,5 |
2,1 |
–0,5 |
1 |
3 |
–0,5 |
2,3 |
1,5 |
–0,3 |
2,9 |
2,1 |
0,7 |
1,2 |
1,8 |
3,3 |
1,4 |
1,6 |
1,5 |
4 |
1,3 |
2,7 |
0,2 |
2,5 |
3 |
2,4 |
0,4 |
2,5 |
0,3 |
0,9 |
0,7 |
2,3 |
1,7 |
5 |
3,5 |
0,9 |
3,2 |
3 |
1,8 |
3,1 |
0,8 |
2,8 |
1,7 |
1,9 |
1,2 |
2,1 |
2 |
6 |
1,2 |
3,7 |
2,3 |
4,2 |
1,4 |
3,2 |
4 |
3,6 |
1,3 |
1,6 |
1,1 |
1,2 |
2,5 |
7 |
3,9 |
1,7 |
4,5 |
2,5 |
1,9 |
4,7 |
4,1 |
1,8 |
3,7 |
3,2 |
2,5 |
1,4 |
3 |
8 |
4,4 |
3 |
2,2 |
2,4 |
5 |
4,2 |
2,3 |
4,6 |
5,2 |
2,6 |
3,3 |
2,8 |
3,2 |
9 |
2,9 |
5,5 |
4,9 |
2,7 |
3,5 |
4,7 |
5,7 |
2,8 |
5,1 |
4,2 |
2,8 |
3,2 |
4 |
10 |
5,3 |
3,1 |
3,9 |
6,1 |
5,9 |
5,1 |
3,3 |
3,2 |
5,5 |
3,8 |
3,3 |
3,1 |
4,5 |
11 |
3,6 |
5,8 |
4,5 |
6,6 |
5,4 |
6,4 |
3,8 |
6,1 |
3,7 |
4,1 |
2,9 |
3,5 |
4,8 |
12 |
4,1 |
6,3 |
4,9 |
7,6 |
5,9 |
6,9 |
4,3 |
6,7 |
4,2 |
3,4 |
4,5 |
3,2 |
5 |
13 |
8,1 |
4,5 |
6,7 |
5,2 |
6,4 |
7,3 |
4,9 |
7,1 |
4,7 |
4,4 |
5 |
4,1 |
5,5 |
14 |
7,2 |
5,1 |
8,5 |
6,9 |
5,7 |
7,8 |
5,4 |
7,6 |
5,2 |
5 |
4,8 |
5,2 |
6 |
15 |
7,7 |
6,3 |
5,6 |
8,9 |
8,3 |
5,9 |
7,4 |
5,7 |
8,1 |
5,3 |
5,9 |
6,1 |
6,5 |
16 |
5,5 |
9,4 |
8,2 |
7,4 |
8,8 |
7,9 |
8,6 |
6,2 |
6,4 |
6,8 |
5,8 |
6,2 |
7 |
17 |
7,1 |
5,7 |
5 |
8,3 |
7,7 |
6,8 |
5,3 |
7,5 |
5,1 |
6 |
5,4 |
5,9 |
6 |
18 |
5,2 |
7,8 |
6,6 |
7,2 |
4,5 |
6,3 |
7 |
4,8 |
4,6 |
5,2 |
5 |
4,8 |
5,3 |
19 |
6,2 |
4,1 |
4,9 |
7,5 |
5,8 |
6,8 |
4,2 |
6,7 |
4,2 |
4,1 |
4,4 |
5 |
4,8 |
20 |
5,7 |
3,5 |
6,5 |
4,4 |
5,3 |
3,7 |
6,3 |
3,6 |
6 |
4,5 |
3,4 |
4,2 |
4,5 |
21 |
3,8 |
5,2 |
2,6 |
5,4 |
5,8 |
5,9 |
3,3 |
5,4 |
3,1 |
3,5 |
4,1 |
2,9 |
4 |
22 |
5,3 |
2,7 |
4,7 |
2,5 |
3,3 |
5,5 |
4,5 |
2,6 |
4,9 |
3,1 |
3,8 |
3,3 |
3,5 |
23 |
2,8 |
4,2 |
1,9 |
5,1 |
2,2 |
4,8 |
4 |
2,1 |
4,4 |
2,8 |
3,2 |
4,2 |
3 |
24 |
3,7 |
1,5 |
4,3 |
1,7 |
3,9 |
2,3 |
1,6 |
4,5 |
3,5 |
3,3 |
2,8 |
2,6 |
2,5 |
25 |
3,4 |
1,1 |
3,7 |
2,1 |
1,2 |
3,8 |
2,9 |
3,4 |
0,9 |
2,6 |
1,4 |
3,2 |
2 |
26 |
0,7 |
3,3 |
2,8 |
3 |
1,6 |
2,9 |
0,5 |
0,6 |
2,6 |
1,6 |
1,1 |
1,2 |
1,5 |
27 |
2,5 |
1,1 |
2,3 |
–0,2 |
2,8 |
2,2 |
0,3 |
0,1 |
2,4 |
2,1 |
1,9 |
1,2 |
1 |
231

28 |
0,4 |
–0,8 |
2 |
1,2 |
–0,6 |
2,6 |
1,8 |
0,9 |
1,5 |
1,1 |
0,7 |
0,9 |
0,5 |
29 |
1,6 |
0,2 |
–0,7 |
1,4 |
–0,9 |
1,9 |
0,8 |
1,2 |
–1 |
1,4 |
3,3 |
1,6 |
0 |
30 |
0,5 |
1,1 |
–0,6 |
–1,8 |
1 |
0,2 |
–0,2 |
1,2 |
0,6 |
0,5 |
–0,5 |
2,1 |
–0,6 |
3.6.6. Проверка гипотезы о равенстве математических ожиданий
|
|
|
Пусть над случайной величинойX |
проделано n |
|
|
независимых |
|||||||||||||||||||||||||
наблюдений, |
в |
которых |
|
получены результатыX1 , X 2 ,¼, X n , |
а |
над |
||||||||||||||||||||||||||
величиной Y проделано m независимых наблюдений и получены значения |
||||||||||||||||||||||||||||||||
Y ,Y ,¼,Y . Предположим, что известны дисперсии D( X ) = s2 и D(Y ) = s2 |
, |
|||||||||||||||||||||||||||||||
1 |
|
2 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
||||
но |
неизвестны |
математические ожиданияМ ( X ) = а1 и |
М (Y ) = а2 . |
Пусть, |
||||||||||||||||||||||||||||
кроме |
того, |
каждая |
серия |
состоит |
|
|
из |
достаточнобольшого |
числа |
|||||||||||||||||||||||
наблюдений (хотя бы несколько десятков в каждой серии). Построим |
||||||||||||||||||||||||||||||||
критерий |
|
для |
проверки по |
результатам |
наблюдений |
гипотезы о том, что |
||||||||||||||||||||||||||
а1 = а2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Предположим, что гипотеза верна. Так как серии опытов достаточно |
|||||||||||||||||||||||||||||
велики, то для средних арифметических имеем приближенные |
равенства |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
» а1 и Y » a2 . Если гипотеза верна, то Х » Y |
и величина | |
Х - Y | |
должна |
||||||||||||||||||||||||||||
быть относительно малой. Напротив, большие значения этой величины |
||||||||||||||||||||||||||||||||
плохо согласуются с гипотезой. Поэтому критическую область составят те |
||||||||||||||||||||||||||||||||
серии |
наблюдений, |
для |
|
|
|
|
|
|
|
С |
–– некоторая |
|||||||||||||||||||||
которых | Х |
- Y |³ С , где |
|||||||||||||||||||||||||||||||
постоянная величина. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Свяжем эту постояннуюC с уровнем значимостиb. Согласно |
|||||||||||||||||||||||||||||
|
|
|
|
|
распределена |
|||||||||||||||||||||||||||
центральной предельной теореме каждая из величин Х |
и Y |
|
||||||||||||||||||||||||||||||
приблизительно |
нормально, |
как |
сумма |
большого |
|
числа |
одинаково |
|||||||||||||||||||||||||
распределенных независимых случайных величин с ограниченными
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дисперсиями. |
С учетом того, что М ( Х ) = M ( X ) и D( Х ) = D( X ) / n, |
можно |
|
||||||||||||||||||||||||
утверждать, |
|
|
|
имеет |
распределениеN (a , s2 / n), a |
|
|
–– |
|
||||||||||||||||||
что Х |
|
Y |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
распределение N (a ,s2 |
/ n). Из |
факта |
устойчивости |
нормального |
закона |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тоже |
|
||||||||||||
распределения можно заключить, что при верной гипотезеХ |
-Y |
|
|
|
|||||||||||||||||||||||
имеет |
нормальный |
закон |
распределения |
|
|
с |
пара |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
s2 / n + s2 / m. |
|
|
|
|
|
|
|
|
||||||||
M ( Х |
- Y ) a =– a |
2 |
0 и D( Х -Y=) |
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|||||||
Запишем для нормального закона распределения N (0,s12 / n + s22 / m) стандартную формулу (????):
æ |
|
|
|
|
|
ö |
|||||
|
|
|
|
ç |
|
|
e |
|
÷ |
||
P(| Х - Y - 0 |< e) =2Fç |
|
|
|
|
÷ |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
ç |
|
|
s2 |
s2 |
÷ |
||||||
ç |
|
|
1 |
+ |
2 |
÷ |
|||||
|
m |
||||||||||
è |
|
|
n |
ø |
|||||||
232
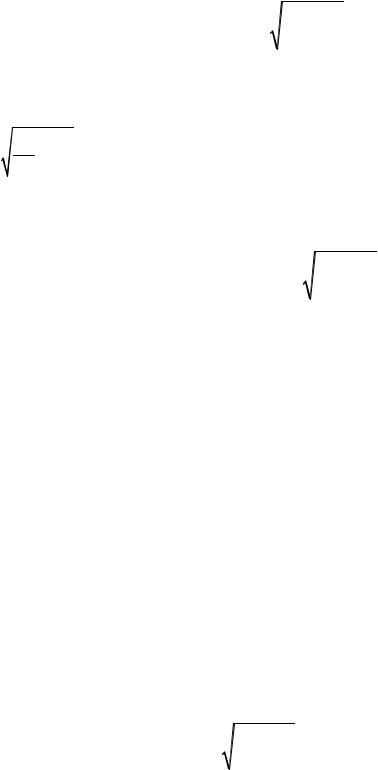
или
æö
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
e |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 –=2Fç |
|
|
|
|
|
|
|
|
|
|
|
|
|
÷. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
P(| Х - Y |³ e) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.6.9) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
s2 |
+ |
s2 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
1 |
2 |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
По |
заданному b из таблицы функции Лапласа(см. прил., табл. П2) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
найдем |
такое tb, |
|
чтобы |
1 – 2F(=t ) |
b |
|
или F(t |
) = |
1 - b |
. |
Тогда |
при |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
e tb |
|
s2 |
|
s2 |
|
правая часть равенства(3.6.9) будет равна b. Поэтому при |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
+ |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
m |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
уровне |
значимости b |
|
|
|
критическую |
|
|
|
область для проверки гипотезы о |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
равенстве двух математических ожиданий составят те серии наблюдений, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
для которых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 |
|
|
|
|
s2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х - Y |
|³ t |
|
|
|
|
|
|
|
|
|
|
|
|
(3.6.10) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
1 |
|
+ |
2 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
n |
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Замечание 1. Если дисперсии неизвестны, то большое число |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
наблюдений |
|
|
в |
|
каждой |
серии |
|
|
позволяет |
достаточно |
точно оценить |
|||||||||||||||||||||||||||||||||||||||||||||||||||
дисперсии по этим же опытным данным: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
)2 |
|
|
|
|||
|
|
|
|
|
|
|
|
D( X ) =s2 |
» |
|
å( X i - X |
|
|
D(Y ) = s2 |
» |
å(Yi - Y |
. |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
и |
i=1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
n -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
m -1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Пример 3.23. Среднее арифметическое результатов 25 независимых |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
измерений некоторой постоянной величины равно90,1. В другой серии из |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
20 независимых измерений получено среднее арифметическое, равное 89,5. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дисперсия ошибок измерения в обоих случаях одинакова и равнаs2 =1, 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
( s »1,1). |
Можно ли считать, что измерялась |
одна |
и |
та |
же |
постоянная |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
величина? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Решение. Выдвигаем гипотезу, что в каждой из серий измерялась |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
одна и та же постоянная величина. Зададимся, |
|
например, |
уровнем |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
значимости |
|
b = 0,01. По |
таблице значений |
функции Лапласа(см. прил., |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
табл. П2) находим, что F(2,58) = |
1 - 0,01 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Тогда критическая область для проверки гипотезы определяется |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
1 |
|
= 0,85. |
Так |
как |
|
в |
нашем |
случае |
|||||||||||||||||||||||||||
неравенством | Х |
- Y |³ 2,58 ×1,1× |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
25 |
20 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
=90,1 –=89,5 |
0,6 < 0,85, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
то сомневаться в том, |
что измерялась одна |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Х |
- Y |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и та же постоянная величина, оснований нет. Расхождения в значениях средних арифметических можно объяснить ошибками измерений.
233
