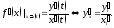3. Производная функции в точке, ее геометрический и механический смысл

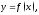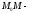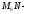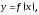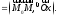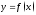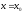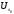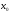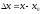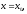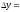На рисунке изображены график функции точкисекущая,касательная к кривойуглыПусть функция определена в точкеи некоторой ее окрестности. Сместимся из точкив точкуВеличинаназываетсяприращением аргумента в точке а величина =называется приращением функции 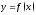в точке 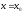(соответствующим приращению 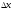аргумента).

Определение 4. Если существует (конечный) предел

то его называют производной функции 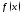в точке 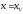и обозначают 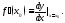При этом функциюназываютдифференцируемой в точке 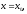а

величину 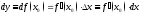называютдифференциалом функции 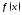в точке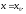

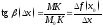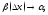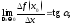Выясним, в чем состоит геометрический смысл производной и дифференциала. Так как и так кактот.е.

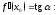производная функции 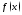в точке является угловым коэффициентом касательной к кривой с точкой касания

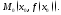
_{С другой стороны, из рисунка видно,что поэтому}

дифференциал 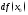равен приращению касательной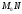к графику функциипри переходе аргумента из точки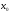в точку

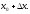
Из геометрического смысла производной легко получить уравнения касательной и нормали к кривой 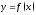в точке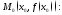

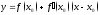(касательная), 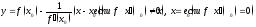(нормаль).

Выясним теперь механический смысл производной. Если 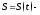путь пройденный материальной точкой за время от момента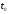до моментатосредняя скорость материальной точки, а величина

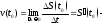мгновенная скорость материальной точки в момент

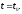
Нетрудно показать, что

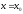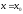любая дифференцируемая в точке функциянепрерывна в точке (обратное, вообще говоря, неверно; пример: непрерывна в точкеноне существует).

4. Арифметические действия над производными

Теорема 4. Если функции 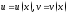дифференцируемы в точке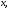то в этой точке дифференцируемы и функции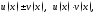причем

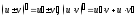(в рассматриваемой точке ).

Если, кроме того, то в точкедифференцируемо и частное, причем

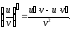
Доказательство проведем для производной суммы. Имеем 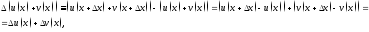поэтому

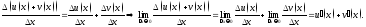Теорема доказана.

5. Производная сложной и обратной функций и функции, заданной параметрически

Приведем без доказательства некоторые утверждения, связанные с производными.

Теорема 5. Пусть сложная функция определена в точкеи некоторой ее окрестност и пусть выполнены условия:

1. функция 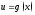дифференцируема в точке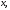

2. функция дифференцируема в соответствующей точке

Тогда сложная функция дифференцирума в точкеи имеет место равенство

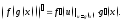
Напомним следующие понятия:

а) Функция 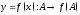называетсяобратимой на множестве 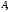если

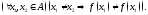
При этом функция 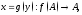сопоставляющая каждому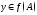элементтакой, что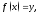называется функцией,обратной к

Очевидно, имеют место тождества:

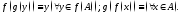
Заметим, что все строго монотонные на множестве 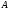функции обратимы на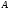

б) Говорят, что функция 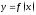задана параметрически уравнениями 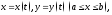если функция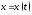обратима на отрезке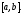В этом случае где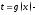функция, обратная к функции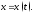

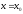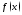Теорема 6. Пусть функция в некоторой окрестности точки имеет обратную функциюПусть, кроме того, функциядифференцируема в точке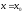и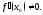Тогда обратная функция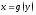дифференцируема в соответствующей точке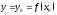и имеет место равенство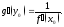

Теорема 7. Пусть функция задана параметрически уравнениями 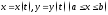и пусть выполнены условия:

1) функции 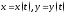дифференцируемы в фиксированной точке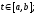

2) 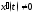в рассматриваемой точке

Тогда функция дифференцируема в точке и имеет место равенство