Абанина Д.А., Коршикова Т.И.-Выпуклые функции

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Федеральное государственное образовательное учреждение высшего профессионального образования

"ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ" Кафедра математического анализа

Д.А. Абанина, Т.И. Коршикова

МЕТОДИЧЕСКИЕ УКАЗАНИЯ к специальному курсу лекций для студентов и слушателей ФПК

факультета математики, механики и компьютерных наук

ВЫПУКЛЫЕ ФУНКЦИИ

Ростов-на-Дону 2008

Введение

Выпуклый анализ достаточно важный и самостоятельный раздел математики, связанный одновременно и с классическим анализом, и с геометрией. Его методы широко применяются в теории функций и комплексном анализе, теории дифференциальных уравнений, вариационном исчислении и теории оптимального управления. Большую роль выпуклость играет также при решении экстремальных задач в современной математической экономике.

Настоящие методические указания посвящены введению в выпуклый анализ. Они включают в себя понятия и основные свойства выпуклых множеств и вы- пуклых функций в RN . Наиболее подробно изучаются выпуклые функции дей-

ствительной переменной. Методические указания состоят из пяти параграфов с теоретическим материалом и примерами решения практических и теоретиче- ских задач. В конце приведены задачи для самостоятельного решения, среди которых "*"отмечены задачи повышенной сложности.

1. Выпуклые множества

Определение 1.1. Множество Q RN называется выпуклым, если

x, y Q , λ [0, 1] λx + (1 − λ)y Q .

Пустое множество считается выпуклым по определению. Условие выпуклости можно записать еще в виде

λ1x1 + λ2x2 Q , x1, x2 Q , λ1, λ2 ≥ 0 , λ1 + λ2 = 1 .

Геометрически выпуклость множества Q означает, что вместе с любыми двумя своими точками Q содержит прямолинейный отрезок, соединяющий эти точки.

Понятно, что выпуклые множества в R это все промежутки, и только они.

Теорема 1.2. Множество Q RN выпукло тогда и только тогда, когда для любого n N справедливо утверждение

λ1x1 + . . . + λnxn Q ,

x1, . . . , xn Q , λ1, . . . , λn ≥ 0 , λ1 + . . . + λn = 1 .

Доказательство. Достаточность очевидна (положите n = 2).

Необходимость будем доказывать индукцией по n. Пусть Q выпукло в RN . Понятно, что при n = 1, 2 рассматриваемое утверждение справедливо. Предположим, что оно верно при некотором n N, и покажем, что тогда оно верно

3

Геометрически рассматриваемое утверждение при n = 3, например, означает, что вместе с любыми тремя своими точками множество Q содержит и соответ-

ствующий треугольник.

В заключение параграфа приведем простейшие свойства выпуклых множеств.

10. Пусть {Qα}α A произвольное семейство выпуклых множеств в RN . Тогда их пересечение Q := T также выпукло.

α A

Доказательство тривиально.

20. Пусть {Qn}∞n=1 расширяющаяся последовательность выпуклых мно-

∞

S

жеств в RN (Q1 Q2 . . .). Тогда их объединение Q := Qn также выпукло.

n=1

Доказательство проведите самостоятельно. Покажите также, что данное утверждение, вообще говоря, перестает быть верным, если нет упорядоченности по вложению.

30. Внутренность int Q и замыкание Q произвольного выпуклого множества выпуклы.

Доказательство. Пусть Q выпукло в RN . Для того чтобы доказать выпуклость множества int Q, возьмем произвольные точки x, y int Q, число λ [0, 1] и покажем, что точка z := λx + (1 −λ)y принадлежит int Q. Òàê êàê x, y int Q,

то найдется ε > 0 такое, что x + B0(ε) Q è y0 + B0(ε) Q. Здесь B0(ε) := {t RN : ktk < ε} открытый шар с центром в 0 радиуса ε. Зафиксируем

произвольное t B0(ε). Тогда x + t Q è y + t Q. Поскольку

z + t = λx + (1 − λ)y + λt + (1 − λ)t = λ(x + t) + (1 − λ)(y + t),

à Q выпукло, то z + t Q. Таким образом, z + B0(ε) Q, òî åñòü z int Q. Выпуклость множества Q докажите самостоятельно.

4

2. Определение и простейшие свойства выпуклых функций

Определение 2.1. Пусть Q выпуклое множество в RN . Функция f : Q → R называется выпуклой, если

x, y Q , λ [0, 1] f λx + (1 − λ)y ≤ λf(x) + (1 − λ)f(y) .

Это условие можно записать также в виде

f(λ1x1 + λ2x2) ≤ λ1f(x1) + λ2f(x2) , x1, x2 Q , λ1, λ2 ≥ 0 , λ1 + λ2 = 1 .

Пример 2.2. Доказать по определению, что функция f(x) = x2 выпукла íà R.

Решение. Для произвольных x, y R è λ [0, 1] имеем

fλx + (1 − λ)y − λf(x) − (1 − λ)f(y) =

=λx + (1 − λ)y 2 − λx2 − (1 − λ)y2 =

=λ2x2 + 2λ(1 − λ)xy + (1 − λ)2y2 − λx2 − (1 − λ)y2 =

=−λ(1 − λ)(x2 − 2xy + y2) = −λ(1 − λ)(x − y)2 ≤ 0 ,

то есть функция x2 выпукла на R.

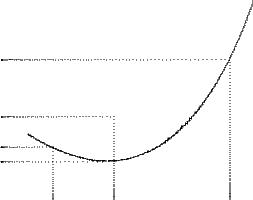
Геометрически выпуклость функции f на интервале (α, β) в R означает, что для любых x1, x2 (α, β), x1 < x2, участок графика функции {(x, f(x)) : x [x1, x2]} лежит не выше хорды, соединяющей точки (x1, f(x1)) è (x2, f(x2)).

Иначе говоря, функция f выпукла вниз в смысле классического математи- ческого анализа, если понятие выпуклости вниз вводить через секущие. В 4

5

будет показано, что если f дифференцируема на (α, β), то выпуклость в смысле

определения 2.1 совпадает также с понятием выпуклости вниз, вводимым через касательные.

Отметим еще, что понятие выпуклой функции можно было определить через надграфик. Именно, функция f выпукла на выпуклом множестве Q RN тогда

и только тогда, когда ее надграфик Epi f := {(x, y) RN+1 : x Q, y ≥ f(x)} является выпуклым множеством в RN+1. В случае N = 1 это легко увидеть на

предыдущем рисунке.

Сформулируем теперь критерий выпуклости Иенсена.

Теорема 2.3. Пусть Q выпуклое множество в RN . Для того чтобы функция f : Q → R была выпукла на Q, необходимо и достаточно, чтобы для любого n N, произвольных точек x1, . . . , xn Q и чисел λ1, . . . , λn ≥ 0 таких, что λ1 + . . . + λn = 1, выполнялось неравенство Иенсена

f(λ1x1 + . . . + λnxn) ≤ λ1f(x1) + . . . + λnf(xn) .

Доказательство аналогично доказательству теоремы 1.2.

Следствие. Если функция f выпукла на выпуклом множестве Q RN , то для любого набора точек x1, . . . , xn Q (n N) выполняется неравенство

Отметим, что первоначально последнее условие выступало в качестве определения выпуклой функции, которое было введено Иенсеном. Взаимосвязь между выпуклостью в смысле определения 2.1 и выпуклостью по Иенсену изучается в5.

Если выписать неравенство Иенсена для конкретных выпуклых функций, можно получить многие известные неравенства анализа (в частности, неравенства Г¼льдера и Минковского). Проиллюстрируем это на примере неравенства между средними арифметическими и средними геометрическими.

6

Решение. Для выпуклой функции ex (строгое доказательство выпуклости ex

проводится с помощью приведенного в 4 критерия выпуклости дважды дифференцируемой функции) неравенство Иенсена имеет вид

Положив здесь xj := ln aj, получим нужное.

Наконец, сформулируем еще интегральное неравенство Иенсена.

Теорема 2.5. Пусть функция f(x) выпукла на выпуклом множестве Q в

x, y Q , λ [0, 1] f λx + (1 − λ)y ≥ λf(x) + (1 − λ)f(y) .

Приведем простейшие свойства выпуклых и вогнутых функций.

10. Пусть Q выпуклое множество в RN . Функция f выпукла на Q тогда и только тогда, когда −f вогнута на Q.

Доказательство тривиально.

20. Функция f одновременно выпукла и вогнута на промежутке I R тогда и только тогда, когда f аффинная функция, то есть f(x) = ax + b.

Доказательство. Достаточность. Åñëè f(x) = ax + b, òî äëÿ âñåõ x, y I è

= λ(ax + b) + (1 λ)(ay + b) = λf(x) + (1 λ)f(y) .

Необходимость. Пусть f выпукла и вогнута на I. Возьмем произвольный отрезок [α, β] I. Зафиксируем x [α, β]. Тогда x = λα + (1 − λ)β, где λ = αx −− ββ .

7

Òàê êàê f выпукла и вогнута на I, òî

=1

получим, что f совпадает с аффинной функцией на всем промежутке I.

30. Пусть Q выпуклое множество в RN , функции f и ϕ выпуклы на Q. Тогда функции f + ϕ и λf, где λ > 0, выпуклы на Q, а функция λf, где λ < 0, вогнута на Q.

Доказательство предлагаем провести самостоятельно.

Замечание. Про разность двух выпуклых функций ничего определенного сказать нельзя. Например, функции f(x) = x2, ϕ(x) = 2x2 выпуклы на R,

ϕ(x) − f(x) = x2 выпукла на R, à f(x) − ϕ(x) = −x2 вогнута на R.

40. Пусть функция f возрастает (соответственно, убывает) на (α, β) и

отображает взаимно однозначно (α, β) на (α1, β1). Доказать, что если f выпукла на (α, β), то обратная функция f−1 вогнута (соответственно, выпук-

ëà) íà (α1, β1).

Доказательство проведите самостоятельно.

50. Пусть ϕ : (α, β) → (α1, β1), f : (α1, β1) → R, ϕ выпукла на (α, β), f

выпукла и не убывает на (α1, β1). Доказать, что f ◦ ϕ выпукла на (α, β).

Рекомендуем доказать этот результат самостоятельно.

60. Пусть A непустое множество индексов, функции fα, α A, выпуклы на выпуклом множестве Q в RN . Тогда множество Q0 := {x Q : sup fα(x) < +∞} выпукло и верхняя огибающая f(x) := sup fα(x) выпукла на

Доказательство. Пусть x, y Q0, λ [0, 1]. Тогда sup fα(x) < +∞ è sup fα(y) <

8

Переходя в последнем неравенстве к супремуму по α A и используя свойства супремумов, получаем, что

≤ sup λfα(x) + sup(1 − λ)fα(y) = λ sup fα(x) + (1 − λ) sup fα(y) < +∞ .

α A α A α A α A

Значит, λx + (1 − λ)y Q0 и f λx + (1 − λ)y ≤ λf(x) + (1 − λ)f(y). Таким образом, f выпукла на Q0.

Совершенно аналогично, учитывая свойства верхних пределов, можно доказать следующее свойство.

70. Пусть функции fk, k N, выпуклы на выпуклом множестве Q в RN è

Следствие. Если последовательность {fk(x)}∞k=1 выпуклых на выпуклом множестве Q в RN функций сходится поточечно на Q к функции f, то f

выпукла на Q.

Заметим, что свойства 60 è 70 перестают быть верными, если супремум за-

менить инфимумом, а верхний предел нижним (задачи 5 и 6).

После изучения данного параграфа рекомендуется решить задачи 1-6.

3. Дифференциальные свойства выпуклой функции действительной переменной

Теорема 3.1. Для того чтобы функция f была выпукла на промежут-

ке I R, необходимо и достаточно, чтобы для любой точки a I наклон

P (MaMx) := f(x) − f(a) был неубывающей функцией по x на I\{a}. x − a

Доказательство. Необходимость. Пусть функция f выпукла на I. Зафиксиру- åì a I è x1, x2 I\{a}, x1 < x2. Возможны три случая.

9

3)x1 < a < x2. Здесь a = λx1 + (1 − λ)x2. Ïðè ýòîì

λ= a − x2 , 1 − λ = x1 − a . x1 − x2 x1 − x2

Используя выпуклость функции f, получаем

Таким образом, во всех трех случаях P (MaMx1 ) ≤ P (MaMx2 ).

Достаточность. Возьмем произвольные x1, x2 I, x1 < x2, и λ [0, 1]. Положим a = λx1 + (1 − λ)x2. Тогда

Так как по условию

(x2 − x1)f(a) ≤ (x2 − a)f(x1) + (a − x1)f(x2) . x2 − x1, получим

f(a) ≤ λf(x1) + (1 − λ)f(x2) ,

10