
1 Статика теория прим реш и 3 задания
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Омский государственный технический университет»
М.В.Силков, А.А.Капелюховский
«Теоретическая механика. Статика»
Методическое указание
к самостоятельной работе студентов
Омск
Издательство ОмГТУ
2014
УДК 531 (075) 3
ББК 22.21 (я 73)
С 36
Рецензент:
З.Н.Соколовский, канд. техн. наук, доц., ОмГТУ.
С36 Теоретическая механика. Статика: метод. указание / М.В.Силков, А.А.Капелюховский – Омск : Изд-во ОмГТУ, 2014. – 31 с.
Данная работа представляет собой методические указания к СРС по разделу «Статика» курса «Теоретическая механика» с необходимой теорией для решения задач, подробным разбором их решения на примерах и прилагаемыми задачами для самостоятельного решения студентами. Основная цель работы объяснение правил и методики решения типовых задач статики.
Работа предназначена для студентов различных форм обучения, но особенно полезна для заочного и дистанционного обучения.
Печатается по решению редакционно-издательского совета
Омского государственного технического университета
УДК 531 (075)
ББК 22.21
© Омский государственный
технический университет, 2014
Основные положения статики
Для решения задач статики просто необходимо знать ряд основных положений, а именно: физический смысл и порядок определения значения для проекции силы, момента силы относительно точки и оси; знать, что такое пара сил и её свойства, уметь составлять уравнения равновесия. Рассмотрим последовательно эти основные положения статики, а затем проиллюстрируем их на примерах решения типовых задач статики.
Проекция силы на ось, характеризует в ньютонах, какая часть данной силы идёт на то, чтобы сдвинуть тело, к которому приложена сила, в направлении выбранной оси. Удобно при решении задач для определения проекции силы предварительно разложить её на составляющие параллельные оси по правилу параллелограмма (рис. 1).

Рис. 1. Разложение
силы
 на составляющие параллельные осям
координат
на составляющие параллельные осям
координат
При этом модули
составляющих сил
 легко найти через заданный модуль
результирующей силы Р
и заданное для неё направление. Направление
силы обычно задаётся углами с осями
(в данном случае это углы
и ).
Используются два прямоугольных
треугольника сил в вертикальной плоскости
АВС
и в горизонтальной ADE.
В этих треугольниках по известной
гипотенузе и углу определяют катеты.
легко найти через заданный модуль
результирующей силы Р
и заданное для неё направление. Направление
силы обычно задаётся углами с осями
(в данном случае это углы
и ).
Используются два прямоугольных
треугольника сил в вертикальной плоскости
АВС
и в горизонтальной ADE.
В этих треугольниках по известной
гипотенузе и углу определяют катеты.
Тогда:
 (1)
(1)

Далее учитываем,
что сила
 есть векторная сумма трёх составляющих,
т.е.
есть векторная сумма трёх составляющих,
т.е.
 ,
поэтому и проекция силы (Рх)
есть алгебраическая сумма трёх проекций
этих составляющих, т.е.
,
поэтому и проекция силы (Рх)
есть алгебраическая сумма трёх проекций
этих составляющих, т.е.
 .
При этом каждая составляющая параллельна
одной оси и перпендикулярна остальным
двум. Если же составляющая перпендикулярная
оси, её проекция на неё равна нулю. Если
составляющая параллельна оси, её проекция
на неё равна модулю составляющей со
знаком «плюс», если она направлена по
оси и «минус», если против оси. Последние
правила легко объясняются физическим
смыслом проекции. Действительно, если
сила перпендикулярна оси, то она не
может сдвинуть тело по этой оси, а если
параллельна, то весь модуль силы
затрачивается на попытку сдвинуть тело
по оси. Знак при этом учитывает направление
сдвига по оси или против.
.
При этом каждая составляющая параллельна
одной оси и перпендикулярна остальным
двум. Если же составляющая перпендикулярная
оси, её проекция на неё равна нулю. Если
составляющая параллельна оси, её проекция
на неё равна модулю составляющей со
знаком «плюс», если она направлена по
оси и «минус», если против оси. Последние
правила легко объясняются физическим
смыслом проекции. Действительно, если
сила перпендикулярна оси, то она не
может сдвинуть тело по этой оси, а если
параллельна, то весь модуль силы
затрачивается на попытку сдвинуть тело
по оси. Знак при этом учитывает направление
сдвига по оси или против.
Таким образом:
 (2)
(2)
При заданных
значениях Р,
,
легко определить в ньютонах значения
проекции силы
 ,
а именно Рх,
Рy,
Рz.
,
а именно Рх,
Рy,
Рz.
Рассмотрим теперь
момент силы относительно точки или оси.
Момент характеризует в ньютонах,
умноженных на метр поворачивающее
действие силы вокруг выбранной точки
или оси. По определению момент силы
относительно точки А
-
 равен векторному произведению радиус
вектора
равен векторному произведению радиус
вектора
 (проводится из точки А к точке приложения
силы) и вектора самой силы
(проводится из точки А к точке приложения
силы) и вектора самой силы
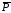 ,
т.е.
,
т.е.
 (3)
(3)
Согласно правилу
векторного произведения результирующий
вектор перпендикулярен плоскости
векторов сомножителей и направлен по
правилу правого винта, если первый
сомножитель
 совмещать со вторым кратчайшим путём
(рис. 2). А модуль вектора
совмещать со вторым кратчайшим путём
(рис. 2). А модуль вектора
 равен произведению модулей векторов
r
и Р,
умноженных на синус угла между ними
(),
т.е.
равен произведению модулей векторов
r
и Р,
умноженных на синус угла между ними
(),
т.е.
 (4)
(4)
где h
– плечо силы, равное длине перпендикуляра,
проведённого из точки А
на линию действия силы
 .
.
Последнее равенство следует из АВС на рис. 2.
Для определения момента относительно оси необходимо спроецировать вектор МА(Р) на эту ось, разложив его на две составляющие параллельную и перпендикулярную оси (рис. 2). Тогда момент относительно оси Z равен
 (5)
(5)


Рис. 2. Определение момента относительно точки или оси
Наиболее просто находить МZ(Р), если ось перпендикулярна силе Р. Тогда = 0, либо = 180 и МZ(Р) = Рh. Поэтому при решении задач для определения момента относительно оси точке удобно раскладывать силу на составляющие параллельные осям (рис. 3).

Рис. 3. Определение момента силы относительно оси
Далее т.к.
 ,
то и момент результирующей
,
то и момент результирующей
 можно найти как сумму моментов составляющих
можно найти как сумму моментов составляющих
 ,
т.е.
,
т.е.
 .
.
Момент параллельной
оси Z
составляющей
 равен нулю,
т.к. в этом случае
= 90 смотри выражение (5). То же следует из
физического смысла момента как оценки
поворачивающего действия силы (сила
параллельная оси не может повернуть
тело вокруг этой оси). Для перпендикулярных
оси Z
составляющих
равен нулю,
т.к. в этом случае
= 90 смотри выражение (5). То же следует из
физического смысла момента как оценки
поворачивающего действия силы (сила
параллельная оси не может повернуть
тело вокруг этой оси). Для перпендикулярных
оси Z
составляющих
 проводим мысленно через них плоскость
Q
и находим точку пересечения её с осью
Z
(точка А
на рис. 3). Из этой точки опускаем
перпендикуляры на линии действия сил
проводим мысленно через них плоскость
Q
и находим точку пересечения её с осью
Z
(точка А
на рис. 3). Из этой точки опускаем
перпендикуляры на линии действия сил
 и
и
 .
Длины этих перпендикуляров и есть плечи
сил
.
Длины этих перпендикуляров и есть плечи
сил
 и
и
 (рис. 3). Модули сил находим по выражениям
(1), а плечи из формул геометрии по заданным
в задаче размерам и углам. Тогда
(рис. 3). Модули сил находим по выражениям
(1), а плечи из формул геометрии по заданным
в задаче размерам и углам. Тогда
 (6)
(6)
Знак «плюс»
ставится для момента силы, если она
поворачивает своё плечо относительно
положительного направления оси против
часовой стрелки (сила
 ),
а знак «минус» - когда по часовой (сила
),
а знак «минус» - когда по часовой (сила
 )
(рис. 3). В частном случае, если сила
пересекает линией действия ось, то плечо
равно нулю, а значит и момент относительно
этой оси равен нулю.
)
(рис. 3). В частном случае, если сила
пересекает линией действия ось, то плечо
равно нулю, а значит и момент относительно
этой оси равен нулю.
Рассмотрим далее понятие пары сил и её свойства. Парой называют две силы, если они параллельны, разнонаправлены и равны по модулю (величине) (рис. 4).
Первым свойством пары является то, что проекция пары на любую ось равна нулю. Т.е. пара не обладает сдвигающим действием, что видно на рис. 4 (силы тянут тело в разные стороны с одинаковым усилием и потому уравновешивают друг друга).
Вторым свойством пары является, то, что её момент относительно параллельных осей одинаков, чего не может быть для одной силы. Рассмотрим это подробнее.
Момент пары это
вектор перпендикулярный плоскости
действия пары и направленный по правилу
правого винта, если смотреть, куда пара
поворачивает тело (рис. 4). Величина
момента М =
Рh,
где h
– плечо пары – перпендикуляр, проведённый
между силами, составляющими пару. Чтобы
найти момент пары относительно оси Z,
надо спроецировать
 на эту ось
на эту ось
 (7)
(7)

Рис. 4. Пара сил и её момент
Из рис. 4 видно, что момент пары относительно параллельных осей будет одинаков.
Учитывая оба свойства пары, часто при решении задач не показывают на расчётной схеме сами силы Р, составляющие пару, а обозначают пару условным значком, задающим величину и направление момента М пары (рис. 5). Это допустимо, т.к. пара характеризуется только моментом. В первых двух картинках показаны пары, расположенные в плоскости рисунка (изгибающий момент), а на последней картинке показан момент пары, перпендикулярный плоскости рисунка (крестик означает, что сила направлена внутрь, а точка – наружу). Здесь изображен крутящий момент
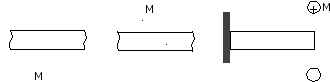
Рис. 5. Примеры условного обозначения пары сил на расчётной схеме
При решении задач, если момент задан в плоскости перпендикулярной оси, например Z, т.е. = 0 или = 180 (см. выражение (7)), то
МZ = Рh. Знак «плюс» соответствует повороту парой тела против часовой стрелки вокруг положительного направления оси, а «минус» - по часовой.
Рассмотрим далее
понятие связи и её реакций. Связями в
механике называют то, что ограничивает
движение тела в пространстве (опоры или
направляющие). Силы, действующие со
стороны связи, на рассматриваемое тело
называются реакции связей. Вид реакций
(сила или пара сил) их число и линии
действия зависят от вида связи. Рассмотрим
ниже основные типовые случаи связей и
их реакций. При этом сначала проанализируем
случай плоского нагружения тела, когда
активные силы
 и реакции лежат в одной плоскости.
Реакции это силы противодействия
активным (заданным) силам. Поэтому,
каково действие (плоское), таково и
противодействие.
и реакции лежат в одной плоскости.
Реакции это силы противодействия
активным (заданным) силам. Поэтому,
каково действие (плоское), таково и
противодействие.
На рис. 6а приведена
опора в виде заделки (запрещает поворот
вокруг оси перпендикулярной плоскости
действия сил). Такая опора может быть
выполнена разными способами: сваркой,
болтами, запрессовкой в отверстие и
т.д. Т.к. опора запрещает поворот и два
взаимно перпендикулярных смещения,
например, по горизонтали и вертикали,
то она создаёт три реакции: пару МА
и две силы
 и
и
 .
На рис. 6б и 6в показаны скользящие
заделки. Первая из них разрешает
перемещение по горизонтали, поэтому
исчезает реакция
.
На рис. 6б и 6в показаны скользящие
заделки. Первая из них разрешает
перемещение по горизонтали, поэтому
исчезает реакция
 .
Вторая разрешает и по горизонтали и по
вертикали, поэтому исчезают
.
Вторая разрешает и по горизонтали и по
вертикали, поэтому исчезают
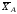 и
и
 .
.

а) б) в)
Рис. 6. Опоры в виде заделки
На рис. 7а показаны
шарнирные опоры, разрешающие поворот
вокруг оси перпендикулярной плоскости
действия сил (не обязательно полный
оборот, достаточно небольшого углового
смещения). Здесь, т.к. запрещены перемещения
по двум взаимно перпендикулярным
направлениям, возникают две взаимно
перпендикулярные реакции
 .
На рис. 7б разрешено перемещение по
одному из двух этих направлений, поэтому
реакция
.
На рис. 7б разрешено перемещение по
одному из двух этих направлений, поэтому
реакция
 исчезает.
исчезает.

а) б) в)
Рис. 7. Опоры шарнирные и опора на невесомый рычаг
На рис. 7в показана опора на невесомый рычаг АА1 (он не нагружен силами и весом можно пренебречь). Такой рычаг работает только на растяжение или сжатие, запрещая перемещение вдоль самого себя. Поэтому он создаёт одну реакцию RА, направленную вдоль самого себя.
На рис. 8а изображена опора на плоскость, а на рис. 8б – на поверхность. В первом случае запрещено перемещение перпендикулярно плоскости вниз, а во втором перпендикулярно касательной к поверхности ВВ1 вниз. Поэтому в обоих случаях возникают по одной реакции RА вдоль направления, по которому опора запрещает движение. На рис. 8в показана опора в виде гибкой связи (трос, цепь, ремень). Работая только на растяжение, такая опора всегда создаёт одну реакцию, направленную вдоль гибкой связи, так чтобы она работала на растяжение.
Направление реакций вдоль их линий действия, кроме случаев на рис. 8, выбирается произвольно, а затем уточняется после решения уравнений равновесия. Если из этих уравнений найдено значение реакции со знаком «плюс», то направление реакций на рис. 6, 7 правильное, а если – «минус», то направление реакция ХА, YА, МА, RА на самом деле противоположно принятому на рисунке.

а) б) в)
Рис. 8. Опора на плоскость, поверхность и гибкая связь
Проанализируем далее случай пространственного нагружения тела. На рис. 9а показана опора в виде заделки. Здесь она запрещает три смещения по осям и три поворота вокруг них и поэтому создаёт шесть реакций. Шарнирные опоры, показанные на рис. 9б запрещают в нижней опоре (втулка с дном) три перемещения по осям, а в верхней – два (по оси Z опора в виде втулки движение разрешает). Поэтому вверху две, а внизу три реакции в виде сил.

Рис. 9. Опора в виде заделки и шарнирные опоры
при пространственном нагружении
Для остальных случаев связей, показанных на рис. 7в и 8 реакции те же, что и при плоском нагружении.
Если при решении задачи необходимо рассматривать равновесие нескольких тел, т.е. разбивать конструкцию, находящуюся в равновесии на несколько твёрдых тел, то надо иметь ввиду, что в месте взаимодействия тел одно из них можно считать связью (опорой) для другого и наоборот. При этом применяется третий закон Ньютона: два тела взаимодействуют с силами равными по величине и противоположными по направлению. Для примера на рис. 10 показано взаимодействие двух тел через скользящую заделку (аналогично будет и для других случаев взаимодействия, рассмотренных на рис. 6, 7, 8, 9).

Рис. 10. Взаимодействие тел 1 и 2 с помощью скользящей заделки
Рассмотрим далее виды и число возможных уравнений равновесия в зависимости от нагружения рассматриваемого тела. Если тело находится в равновесии и заданы активные силы, необходимо добавить (нарисовать) к ним реакции всех связей данного тела и посмотреть на вид полученной системы сил. Когда получилась пространственная произвольная система сил, то для тела можно составить шесть уравнений равновесия, а именно: сумма проекций всех сил на три оси координат равна нулю и сумма моментом всех сил относительно трёх этих осей равна нулю. Эти уравнения справедливы, т.к. в равновесии тело не может смещаться по осям и поворачиваться вокруг них. В общем виде уравнения выглядят так:
 (8)
(8)
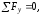 (9)
(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)
 (13)
(13)
Чтобы составлять эти уравнения для конкретной задачи надо использовать приёмы и правила, рассмотренные выше для определения проекций и моментов сил и пар сил.
Рассмотрим частные случаи.
1. Параллельная система сил, когда все силы параллельны, например, оси Z. Тогда на оси Х и Y проецировать нечего, т.к. все силы им перпендикулярны и уравнения (8) и (9) не используются. Кроме того, моменты относительно оси Z для всех сил равны нулю, т.к. они параллельны Z и уравнение (13) не используется. Остаются три уравнения (10), (11), (12).
2. Сходящаяся система сил, когда линии действия всех сил сходятся в одной точке. В эту точку можно поместить начало координат и тогда все силы пересекают все оси, а потому их моменты равны нулю. Остаются для использования только уравнения проекций (8), (9), (10).
3. Плоская система
сил, например, все силы лежат в плоскости
ХY.
Тогда на ось Z
нечего проецировать. А кроме того силы
либо пересекают оси Х и Y
либо параллельны одной из них, а значит
моменты относительно этих осей для всех
сил равны нулю. Таким образом, можно
использовать три уравнения (8), (9), (13).
При этом, при плоском нагружении (плоская
статика) не принято рисовать ось Z
и уравнение (13) записывается так
 .
Здесь точка А – это точка пересечения
оси Z
с плоскостью действия сил Х и Y,
причём начало координат осей Х и Y
может не совпадать с этой точкой (при
пространственном нагружении обязательно
все три оси выходят из одного начала
координат).
.
Здесь точка А – это точка пересечения
оси Z
с плоскостью действия сил Х и Y,
причём начало координат осей Х и Y
может не совпадать с этой точкой (при
пространственном нагружении обязательно
все три оси выходят из одного начала
координат).
Таким образом, в общем случае шесть уравнений равновесия, но в частных случаях их меньше. Мы рассмотрели три частных случая, когда их три, но может любое другое число от пяти до одного в зависимости от вида нагружения. Чтобы правильно определить число возможных уравнений, надо знать и применять правила, когда проекция или момент силы относительно оси равны нулю.
В заключение рассмотрим, при каких условиях реальную пространственную конструкцию можно заменить плоской расчётной схемой. Это справедливо, если конструкция или одно тело обладает плоскостью симметрии, а кроме того все заданные нагрузки и опоры симметричны этой плоскости либо расположены в ней.
На рис. 11, а показано пространственное твёрдое тело с нагрузками и опорами, подчиняющимися этому условию. На рис. 11, б показана эквивалентная плоская расчётная схема для этого тела. При этом при переходе к плоской схеме две силы Р1 заменяются одной удвоенной по значению. Также две опоры в точках А1, А2 заменяются одной опорой. Затем при определении реакций в этой опоре А их можно разделить пополам для опор А1 и А2 (в этом и состоит упрощение при переходе к плоской расчётной схеме).
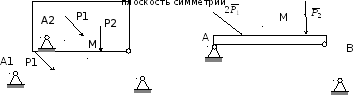
а) б)
Рис. 11. Переход от пространственной к плоской расчётной схеме из-за симметрии тела, нагрузок и опор
Ниже приведены примеры решения основных типовых задач статики с подробными пояснениями последовательности и хода решения. Здесь же приведены варианты заданий для самостоятельного решения.
Задача-1. Определение реакций опор одного твердого тела, нагруженного плоской системой внешних сил.
На рисунках показаны расчетные схемы с внешними нагрузками и размерами, заданными для каждого варианта в таблице, расположенной рядом со схемой. Необходимо определить реакции опор.
Дано: вариант расчетной схемы (рис. 1); Р1 = 8 кН; Р2 = 10 кН; q = 12 кН/м; М = 16 кН∙м; ℓ = 0,1 м.
Определить реакции в опорах А и В.

Рис. 1
Решение. Заменяем действие связей (опор) реакциями. Число, вид (сила или пара сил с моментом), а также направление реакций зависит от вида опор. В плоской статике для каждой опоры в отдельности можно проверить, какие направления движения запрещает телу данная опора. Проверяют два взаимно перпендикулярных смещения тела относительно опорной точки (А или В) и поворот тела в плоскости действия внешних сил относительно этих точек. Если запрещено смещение то будет реакция в виде силы по этому направлению, а если запрещен поворот, то будет реакция в виде пары сил с моментом (МА или МВ).
Первоначально реакции можно выбирать в любую сторону. После определения значения реакции знак «плюс» у него будет говорить о том, что направление в эту сторону верное, а знак «минус» – о том, что правильное направление реакции противоположно выбранному (например, не вниз, а вверх для силы или по часовой стрелке, а не против неё для момента пары сил).
Исходя из вышесказанного, показаны реакции на рис. 1. В опоре А их две, т. к. опора запрещает перемещение по горизонтали и вертикали, а поворот вокруг точки А разрешает. Момент МА не возникает, т. к. это шарнирная опора не запрещает поворот телу вокруг точки А. В точке В одна реакция, т. к. запрещено перемещение только в одном направлении (вдоль невесомого рычага ВВ).
Далее перед составлением уравнения равновесия тела необходимо на рис. 1 провести следующие дополнительные построения, упрощающие последующую работу.
Во-первых,
распределенная нагрузка q
заменяется эквивалентной сосредоточенной
силой
 .
Линия действия её проходит через центр
тяжести эпюры (для прямоугольной эпюры
центр тяжести на пересечении диагоналей,
поэтому сила Q
проходит через середину отрезка, на
который действует q).
Величина силы Q
равна площади эпюры, т. е.
.
Линия действия её проходит через центр
тяжести эпюры (для прямоугольной эпюры
центр тяжести на пересечении диагоналей,
поэтому сила Q
проходит через середину отрезка, на
который действует q).
Величина силы Q
равна площади эпюры, т. е.
Q = q∙2ℓ = 12∙2∙0.1 = 2.4 кН.
Затем необходимо
выбрать оси координат x
и y
и разложить все силы и реакции не
параллельные осям на составляющие
параллельные им, используя правило
параллелограмма. На рис. 1 разложены
силы
 .
При этом точка приложения результирующей
и её составляющих должна быть одна и та
же. Сами составляющие можно не обозначать,
т. к. их модули легко выражаются через
модуль результирующей и угол с одной
из осей, который должен быть задан либо
определен по другим заданным углам и
показан на схеме. Например для силы Р2
модуль горизонтальной составляющей
равен Р2cos60
(т.к. это прилежащий катет в силовом
прямоугольном треугольнике), а вертикальной
Р2sin60
(т.к. это противолежащий катет в силовом
треугольнике).
.
При этом точка приложения результирующей
и её составляющих должна быть одна и та
же. Сами составляющие можно не обозначать,
т. к. их модули легко выражаются через
модуль результирующей и угол с одной
из осей, который должен быть задан либо
определен по другим заданным углам и
показан на схеме. Например для силы Р2
модуль горизонтальной составляющей
равен Р2cos60
(т.к. это прилежащий катет в силовом
прямоугольном треугольнике), а вертикальной
Р2sin60
(т.к. это противолежащий катет в силовом
треугольнике).
Далее необходимо применить правила определения проекции силы на ось и момента силы относительно оси. Проекция или момент результирующей силы, например Р2 , равен сумме проекций или моментов составляющих Р2cos60 и Р2sin60.
Для каждой составляющей проекция находиться так: если составляющая перпендикулярна оси, то проекция ее на эту ось равна нулю, а если она параллельна оси, то проекция равна ее модулю со знаком плюс, если она совпадает по направлению с осью и со знаком минус, если она по направлению противоположна оси. Например для силы Р2 , получим проекция ее на ось X: Р2x =- Р2cos60, на Y: Р2y =- Р2sin60.
Для определения момента силы применяется следующее правило. Момент силы параллельной оси равен нулю. Момент силы перпендикулярной оси находиться как произведение ее модуля на плечо. Со знаком плюс момент берется, если сила стремится повернуть свое плечо против часовой стрелки и со знаком минус, если по часовой (смотреть надо с положительного направления оси). Плечо силы это длина перпендикуляра, проведенного от оси на линию действия силы. Иногда удобней искать плечи для каждой составляющей, чем для результирующей, как например для силы Р2. В результате для горизонтальной составляющей момент относительно оси Z перпендикулярной плоскости рисунка и проходящей через точку А равен
MA
= ,
,
а для вертикальной составляющей
MA
=
 ,
,
где в скобках – плечи сил. Они находятся из геометрии как сумма или разность отрезков (заданных или определяемых как катеты прямоугольных треугольников по известной гипотенузе и углу; прилежащий к углу катет находится как произведение гипотенузы на косинус этого угла, а противолежащий - как произведение гипотенузы на синус). Для силы Р1 применяя эти правила получим для горизонтальной составляющей
MA
=
 ,
,
а для вертикальной
MA
=
 .
.
Для пары сил проекция на любую ось равна нулю, а момент пары относительно любой оси, перпендикулярной плоскости пары, равен плюс или минус М, где М заданный момент пары (плюс, если пара поворачивает тело против часовой стрелки и минус – по часовой).
Теперь можно
составить три уравнения равновесия, а
т. к. неизвестных реакций тоже три
 ,
их значения легко находятся из этих
уравнений. Знак у значения реакции, о
чем говорилось выше, определяет
правильность выбранных направлений
реакций. Для схемы на рис. 1 уравнения
проекций всех сил на оси х
и y
и уравнения моментов всех сил относительно
точки А
запишутся так
,
их значения легко находятся из этих
уравнений. Знак у значения реакции, о
чем говорилось выше, определяет
правильность выбранных направлений
реакций. Для схемы на рис. 1 уравнения
проекций всех сил на оси х
и y
и уравнения моментов всех сил относительно
точки А
запишутся так

Из первого уравнения находим значение RB, затем подставляем его со своим знаком в уравнения проекций и находим значения реакций ХА и YА .
В заключении отметим, что удобно уравнение моментов составлять относительно той точки, чтобы в нем оказалась одна неизвестная реакция, т. е. чтобы эту точку пересекали две другие неизвестные реакции. Оси же удобно выбирать так чтобы большее число сил оказались параллельны осям, что упрощает составление уравнений проекций.
