Вопросы МатЛогика

№1 Высказывания. Логические операции

Высказывание — повествовательное предложение, выражающее суждение. Может быть истинным или ложным. Операции: отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ), также есть дополнительные операции, такие как эквиваленция («тогда и только тогда, когда»), импликация («следовательно»). Таблицы истинности составить самостоятельно

№2 Формулы алгебры высказываний

В формулу вместо переменных можно подставлять конкретные высказывания, после чего вся формула будет превращаться в некоторое составное высказывание.

• Каждая отдельно взятая пропозициональная переменная есть формула алгебры высказываний.

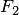• Если и — формулы алгебры высказываний, то выражения также являются формулами алгебры высказываний:

• Никаких других формул алгебры высказываний, кроме получающихся согласно пунктам 1 и 2, нет.

№3 Равносильность формул. Равносильные формулы

Формулы и алгебры высказываний называются равносильными (эквивалентными), если при любых значениях входящих в них пропозициональных переменных логические значения получающихся из формул и высказываний совпадают

Равносильные формулы

1. НЕ НЕ A ≡ A – двойное отрицание

2. A ∧ A ≡ A

3. A ∨ A ≡ A

4. A ∧ B ≡ B ∧ A

5. A ∨ B ≡ B ∨ A

6. A ∧ (B ∧ C) ≡ (A ∧ B) ∧ C

7. A ∨ (B ∨ C) ≡ (A ∨ B) ∨ C

8. A ∧ (B ∨ C) ≡ (A ∧ B) ∨ (A ∧ C)

9. A ∨ (B ∧ C) ≡ (A ∨ B) ∧ (A ∨ C)

10. A ∧ B ≡ НЕ A ∨ НЕ B

11. A ∨ B ≡ НЕ A ∧ НЕ B

12. A ∧ НЕ A ≡ 0

13. A ∨ НЕ A ≡ 1

14. A ∧ 1 ≡ A

15. A ∨ 0 ≡ A

16. A ∧ 0 ≡ 0

17. A ∨ 1 ≡ 1

18. A ∧ (A ∨ B) ≡ A

19. A ∨ (A ∧ B) ≡ A

20. A → B ≡ НЕ A ∨ B

21. A → B ≡ НЕ B → НЕ A

22. A ↔ B ≡ (A → B) ∧ (B → A)

№4 Алгебра Буля. Примеры алгебры Буля

Булевой алгеброй (алгебраическая система) называется непустое множество A с двумя бинарными операциями (аналог конъюнкции), (аналог дизъюнкции), унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:

		ассоциативность
		коммутативность
		законы поглощения
		дистрибутивность
		дополнительность

Первые три аксиомы означают, что (A, , ) является решёткой. Таким образом, булева алгебра может быть определена как дистрибутивная решётка, в которой выполнены две последние аксиомы.

№5 Типы формул высказываний

Формулы алгебры высказываний подразделяются на следующие типы: выполнимые, тавтологии, опровержимые и тождественно ложные.

Формула алгебры высказываний называется выполнимой, если некоторая ее конкретизация является истинным высказыванием, т.е. , выполнима, если существуют такие конкретные высказывания , что .

Формула называется тавтологией, или тождественно истинной, если она превращается в истинное высказывание при всякой подстановке вместо переменных конкретных высказываний , т.е. если для любых высказываний .

Формула называется опровержимой, если существуют такие конкретные высказывания , которые превращают данную формулу в ложное высказывание , т.е. .

Наконец, формула называется тождественно ложной, или противоречием, если для любых конкретных высказываний .

№6 Тавтология и равносильность. Основные правила получение тавтологий

Тавтологии представляют собой схемы построения истинных высказываний, независимо от содержания и истинности составляющих высказываний.

(правило заключения). Если формулы и являются тавтологиями, то формула также тавтология. Другими словами, из и следует

правило подстановки). Если формула , содержащая пропозициональную переменную , является тавтологией, то подстановка в формулу вместо переменной любой формулы снова приводит к тавтологии. Другими словами, из следует .

№7 Закон двойственности

Если в формуле F, представляющей функцию  f, все конъюнкции заменить на дизъюнкции, дизъюнкции на конъюнкции,  1  на  0,  0  на  1, то получим формулу F*, представляющую двойственную функцию   f*.

№8-11 ДНФ, КНФ, СДНФ, СКНФ

Конъюнктивным одночленом от переменных называется конъюнкция этих переменных или их отрицаний.

Дизъюнктивным одночленом от переменных называется дизъюнкция этих переменных или их отрицаний

Дизъюнктивной нормальной формой называется дизъюнкция конъюнктивных одночленов, т.е. выражение вида , где все , являются конъюнктивными одночленами (не обязательно различными).

Конъюнктивной нормальной формой называется конъюнкция дизъюнктивных одночленов , где все , являются дизъюнктивными одночленами (не обязательно различными).

Нормальную форму, представляющую формулу (то есть равносильную ), будем называть просто нормальной формой этой формулы.

Среди множества дизъюнктивных (равно как и конъюнктивных) нормальных форм, существует уникальная форма: она единственна для данной формулы. Это так называемая совершенная дизъюнктивная нормальная форма (среди конъюнктивных форм — совершенная конъюнктивная нормальная форма).

Одночлен (конъюнктивный или дизъюнктивный) от переменных называется совершенным, если в него от каждой пары входит только один представитель ( или ). НФ (дизъюнктивная или конъюнктивная) от переменных называется совершенной от этих переменных, если в нее входят лишь совершенные одночлены

№12 Логическое следование. Признаки логического следствия

Формула называется логическим следствием формул , если формула превращается в истинное высказывание при всякой такой подстановке вместо всех ее пропозициональных переменных конкретных высказываний, при которой в истинное высказывание превращаются все формулы . То, что формула является логическим следствием формул , записывается так: . Формулы называются посылками для логического следствия .

То, что некоторая формула является логическим следствием каких-то формул, можно выразить так же, сказав, что подходящая формула является тавтологией.

(признак логического следствия). Формула Н будет логическим следствием формулы тогда и только тогда, когда формула является тавтологией: .

Следующая теорема дает признаки того, что формула является логическим следствием двух или большего количества формул.

Для любых формул следующие утверждения равносильны:

а) ; б) ; в) .

№13 Классификация математических предложений(теорем)

Многие математические теоремы имеют структуру, выражаемую формулой . Утверждение называется условием теоремы, а утверждение — ее заключением.

Далее, если некоторая теорема имеет форму , утверждение называется обратным для данной теоремы. Это утверждение может быть справедливым, и тогда оно называется теоремой, обратной для теоремы , которая, в свою очередь, называется прямой теоремой. Если же утверждение не выполняется, то говорят, что обратная теорема для теоремы неверна.

С понятиями прямой и обратной теорем тесно связан вопрос о необходимых и достаточных условиях. Если некоторая математическая теорема имеет структуру, выражаемую формулой , то высказывание называется необходимым условием для высказывания (другими словами, если истинно, то с необходимостью должно быть также истинным), а высказывание называется достаточным условием для высказывания (другими словами, для того чтобы было истинным, достаточно, чтобы истинным было высказывание ).

ля теоремы, сформулированной в виде импликации , кроме обратного утверждения можно сформулировать противоположное утверждение. Им называется утверждение вида . Утверждение, противоположное данной теореме, может быть также теоремой, т. е. быть истинным высказыванием, но может таковым и не быть. Это следует из того, что формулы и .Уне являются равносильными

Остается рассмотреть еще один вид теорем, связываемых с прямыми теоремами вида , и установить взаимоотношения между этими видами. Имеется в виду теорема, обратная противоположной: . Мы не случайно назвали теоремой утверждение, обратное противоположному. Оно действительно будет истинным тогда и только тогда, когда истинно исходное утверждение, что вытекает из равносильности (см. теорему 4.4, пункт б)), называемой законом контрапозиции. Таким образом, на основании закона контрапозиции предложение, обратное какой-либо противоположной теореме, само является теоремой, и вместо доказательства данной теоремы можно доказывать теорему, обратную противоположной ей.

№14 Формализованное исчисление высказываний

Из всех формул алгебры высказываний выделяется некоторая часть. Формулы из этой части объявляются аксиомами. Определяется некоторое правило, по которому из одних формул можно получать новые. Таким образом, тавтологии алгебры высказываний оказываются теоремами аксиоматической теории, в результате получаем аксиоматическое построение алгебры высказываний.

К первоначальным, неопределяемым понятиям аксиоматической теории высказываний относятся следующие: — пропозициональные переменные; — логические связки; — технические знаки. Первоначальным понятием является также понятие формулы:

1) каждая пропозициональная переменная есть формула; 2) если и — формулы, то выражения также являются формулами;

В качестве аксиом выбираются формулы следующих видов

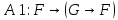
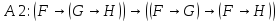
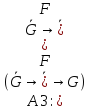
Единственным правилом вывода будет служить правило заключения (или отделения, или modus ponens, или сокращенно ): из формул и непосредственно следует формула .

Для определения некоторых связок используем:

означает ; означает ; означает .

№15 Теория формального вывода. Свойства выводимости

Доказательством или выводом формулы из множества формул называется такая конечная последовательность формул, каждая формула которой является либо аксиомой, либо формулой из , либо получена из двух предыдущих формул этой последовательности по правилу , а последняя формула совпадает с .

Если имеется вывод формулы из множества , то говорят, что выводима из и пишут . Элементы из называются гипотезами или посылками вывода. Если же имеется вывод формулы из пустого множества гипотез, то говорят, что выводима из аксиом. Саму называют теоремой, и пишут . Если множество конечно: , то вместо будем писать .

(свойства выводимости).

а) Если и , то ;

б) тогда и только тогда, когда в существует такое конечное подмножество , что ;

в) Если для любой формулы из множества и , то .

№16 Теорема о дедукции

Если , то . В частности, если , то

Следствие тогда и только тогда, когда

Лемма Для любых формул справедливы следующие выводимости:

а) ; б) .

Для любых формул следующие формулы являются теоремами формализованного исчисления высказываний:

а) ; б) ; в) ; г) ; д) ; е) ; ж) .

№17 Логика предикатов. Классификация предикатов

предикат , определенный на множествах , превращается в конкретное высказывание, если вместо предметных переменных подставить в него конкретные предметы (элементы ) из множеств соответственно. Это высказывание может быть либо истинным, либо ложным, т. е. его логическое значение равно 1 или 0. Следовательно, данный предикат определяет функцию аргументов, заданную на множествах принимающую значение в двухэлементном множестве . Поэтому предикат называют также функцией-высказыванием.

___________________________________________________________________________________

Пример: Предложение "Река впадает в озеро Байкал" является одноместным предикатом, определенным над множеством всех названий рек. Подставив вместо предметной переменной название "Баргузин", получим высказывание "Река Баргузин впадает в озеро Байкал". Это высказывание истинно. Подставив вместо предметной переменной название "Днепр", получим ложное высказывание "Река Днепр впадает в озеро Байкал".

____________________________________________________________________________________

Предикат классифицируют на:

а) тождественно истинным, если при любой подстановке вместо переменных любых конкретных предметов из множеств соответственно он превращается в истинное высказывание ;

б) тождественно ложным, если при любой подстановке вместо переменных любых конкретных предметов из множеств соответственно он превращается в ложное высказывание;

в) выполнимым (опровержимым), если существует по меньшей мере один набор конкретных предметов из множеств соответственно, при подстановке которых предикат превратится в истинное (ложное) высказывание .