§ 7.5. Линейные операторы простой структуры

Линейный оператор , действующий в - мерном линейном пространстве , называется оператором простой структуры, если в пространстве существует базис, состоящий из собственных векторов этого оператора. В силу § 7.1 в базисе из собственных векторов матрица оператора простой структуры имеет вид

, (7.5.1)

где - собственные значения оператора.

Если в исходном базисе оператор простой структуры имеет матрицу , а в базисе из собственных векторов - матрицу , то в силу соотношения (7.3.2) из § 7.3 имеем

, (7.5.2)

где - матрица перехода от базиса к базису . Она состоит из столбцов координат базиса в базисе , - матрица вида (7.5.1). На матричном языке соотношение (7.5.2) означает, что матрица приводится матрицей к диагональному виду.

Разрешив соотношение (7.5.2) относительно матрицы , получим соотношение

, (7.5.3)

которое называется каноническим разложением матрицы .

При построении матрицы для соотношений (7.5.2) и (7.5.3) нужно найти все собственные значения матрицы и при каждом собственном значении построить фундаментальную систему решений однородной системы уравнений ; из векторов всех построенных фундаментальных систем решений, как из столбцов, составить матрицу . Причём в матрице столбцами записываются решения по каждому в порядке нумерации собственных значений (одинаковые считаются столько раз, каковы их алгебраические кратности). Если матрица окажется квадратной, то она будет удовлетворять соотношениям (7.5.2) и (7.5.3). Если же матрица окажется неквадратной, то соотношения (7.5.2) и (7.5.3) для матрицы будут невозможны, т.е. матрица не приводится к диагональному виду и, следовательно, не имеет канонического разложения.

Матрица будет квадратной лишь в случае, когда оператор с матрицей является оператором простой структуры. В соответствии с критерием простоты структуры линейного оператора для того, чтобы оператор имел простую структуру, необходимо и достаточно, чтобы для каждого его собственного значения алгебраическая кратность совпадала с геометрической кратностью, т.е. с максимальным числом линейно независимых собственных векторов матрицы по , равным , где - ранг матрицы . Справедлив следующий достаточный признак простой структуры линейного оператора: если все собственные значения линейного оператора попарно различны, то он имеет простую структуру.

Пример. Выясните, является ли оператор, действующий в действительном трёхмерном линейном пространстве, с матрицей оператором простой структуры. Если да, то найдите матрицу , трансформирующую матрицу к диагональному виду, и запишите этот вид.

Решение. Составим характеристический многочлен матрицы :

. Решив характеристическое уравнение , получим собственные значения , и соответствующие им алгебраические кратности , . Найдём базисы собственных подпространств линейного оператора, попутно проверив, выполняется ли критерий простоты структуры оператора.

.

Геометрическая кратность первого собственного значения равна и совпадает с алгебраической кратностью . Общий вид собственных векторов, отвечающих , таков: . Полагая последовательно , и , , получаем базис первого собственного подпространства: ; .

Геометрическая кратность второго собственного значения равна и совпадает с алгебраической кратностью . Таким образом, критерий простоты структуры линейного оператора выполняется. Общий вид собственных векторов, отвечающих , таков : . Выбирая , получаем базис второго собственного подпространства:

. В базисе линейный оператор имеет матрицу 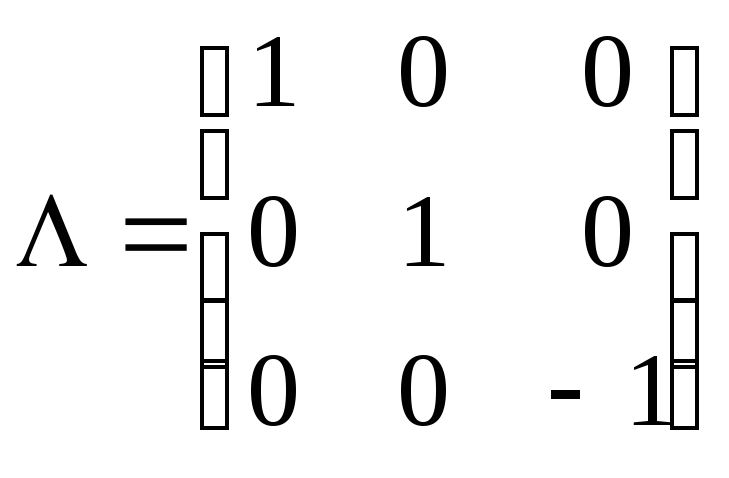и трансформирующая матрица . Проверим это:

.

7.5.1. Квадратная матрица называется матрицей простой структуры, если она подобна некоторой диагональной матрице. Докажите, что оператор из тогда и только тогда будет оператором простой структуры, когда его матрица в произвольном базисе пространства является матрицей простой структуры.

7.5.2. Покажите, что операторы проектирования и операторы отражения имеют простую структуру.

7.5.3. Докажите, что если матрица имеет простую структуру, то это же верно в отношении транспонированной матрицы .

7.5.4. Пусть - линейный оператор, действующий в конечномерном линейном пространстве . Докажите, что следующие высказывания равносильны:

- оператор простой структуры;

объединение базисов собственных подпространств является базисом в ;

алгебраическая кратность каждого корня характеристического уравнения равна размерности соответствующего собственного подпространства;

является прямой суммой собственных подпространств.

7.5.5. Докажите, что у оператора простой структуры:

образ есть линейная оболочка собственных векторов, относящихся к ненулевым собственным значениям;

пересечение ядра и образа состоит только из нулевого вектора.

7.5.6. Выясните, какие из матриц линейных операторов в пространстве над можно привести к диагональному виду путем перехода к новому базису. Найдите этот базис и соответствующую ему матрицу:

а) б) в)

г) д) е)

7.5.7. Подобна ли матрица

а) б) в)

диагональной матрице?

7.5.8. Для каждой из приведенных ниже матриц над полем выясните, является ли оператор с данной матрицей оператором простой структуры:

а) б) в)

г) д)

Если да, то найдите матрицу , трансформирующую эту матрицу к диагональному виду и укажите этот вид.