
- •Оглавление.
- •Пример 1
- •Пример 2
- •Пример 3
- •Вопрос.
- •Глава I Математический формализм
- •О понятии действительных чисел
- •Формализм натуральных чисел.
- •Операции, определяющие формирование множества рациональных чисел.
- •Вывод 1.
- •Вывод 2.
- •Аксиома связи сложения и умножения.
- •Задача 2.
- •Вывод 3.
- •Аксиоматизация множества действительных чисел.
- •Аксиома непрерывности Кантора.
- •Аксиоматическое обоснование евклидовой геометрии.
- •О“Началах” Евклида.
- •Аксиоматика д. Гильберта(1862-1943)
- •Группа 1. Аксиомы соединения.
- •Теорема 1.
- •Теорема 2.
- •Теорема 3.
- •Группа 2. Аксиомы порядка.
- •Определение.
- •Группа 3. Аксиомы конгруэнтности.
- •Теорема (о внешнем угле треугольника).
- •Определение движения.
- •Замечание 1.
- •Вывод 1.
- •Вывод 2.
- •Группа 4. Аксиомы непрерывности.
- •Замечание 2.
- •Замечание 3.
- •Вывод 3.
- •Группа 5. Аксиома параллельности.
- •Замечание 4.
- •Два недостатка аксиоматики д. Гильберта.
- •Структура векторного пространства.
- •Модель направленных отрезков.
- •Сложение обладает свойствами:
- •Свойства операции умножения:
- •Определение.
- •Арифметическая модель векторного пространства.
- •Теорема размерности.
- •Вывод 1.
- •Вывод 2.
- •Вывод 3.
- •Аксиомы скалярного произведения векторов.
- •Следствие.
- •Следствие.
- •Вывод 4.
- •Определение.
- •Модель Вейля евклидовой геометрии.
- •Арифметизация трехмерного евклидова пространства.
- •Свойства операции откладывания вектора.
- •Определение.
- •Вывод 1.
- •Вывод 2.
- •Многомерное арифметическое евклидово пространство.
- •Вывод 3.
- •Замечание.
- •Следствие 1.
- •Основные факты в планиметрии Лобачевского.
- •1. Сумма углов многоугольника в плоскости l2.
- •Следствие 2.
- •Вывод 3.
- •Главаii Свойства аксиоматических систем.
- •Математические структуры и аксиоматические теории.
- •Понятие отношений между объектами.
- •Следствие 1.
- •Пример 1.
- •Определение.
- •Следствие 2.
- •Понятие математической структуры.
- •Определение.
- •Замечание 1.
- •Формальная и содержательная аксиоматики. Теории и структуры.
- •Рассмотрим пример.
- •Вывод 1.
- •Вывод 2.
- •Определение.
- •Изоморфизм.
- •Пример 1.
- •Пример 2.
- •Определение изоморфизма.
- •Вывод 3.
- •Вывод 1.
- •Независимость аксиоматической системы.
- •Независимость аксиомы параллельности.
- •Замечание 1.
- •Дедуктивная полнота и категоричность системы аксиом.
- •Определение (дедуктивной полноты).
- •Определение (категоричности).
- •Историческая роль V постулата Евклида в развитии оснований математики.
- •Анализ текстовых парадоксов.
- •Языковые свойства имен объектов.
- •Пример 1.
- •Пример 2.
- •Пример 3.
- •Проблема выразимости.
- •Понятие искусственного языка.
- •Понятие парадокса.
- •“Ахиллес и черепаха”.
- •Парадокс пустого множества.
- •Парадокс достижимости в натуральном ряде.
- •“Одно и то же, но по-разному”
- •Пример 1.
- •Пример 2.
- •Заключение.
- •Обозначения.
- •Литература
Вывод 1.
Если
в пространстве задан базис {![]() 1,
1,![]() 2,
2,![]() 3},
то между множеством векторов и
упорядоченными тройками чисел (x,y,z)
установлено взаимно-однозначное
соответствие
3},
то между множеством векторов и
упорядоченными тройками чисел (x,y,z)
установлено взаимно-однозначное
соответствие
![]() ↔(x,y,z),
(1)
↔(x,y,z),
(1)
определяемое
разложением вектора
![]() в заданном базисе:
в заданном базисе:![]() .
.
Чтобы
объявить множество упорядоченных троек
чисел
![]() арифметической или координатной моделью
трехмерного векторного пространства,
покажем, что операции сложения векторов
и умножения на число определена в
координатной форме и, что координаты
вектора определяют его длину и направление.
арифметической или координатной моделью
трехмерного векторного пространства,
покажем, что операции сложения векторов
и умножения на число определена в
координатной форме и, что координаты
вектора определяют его длину и направление.
Для
удобства будем считать, что
![]() ,
,![]() ,
,![]() – известный в элементарной геометрии
базис, состоящий из единичных
взаимно-перпендикулярных векторов. Для
простоты, также, ограничимся случаем
плоскости.
– известный в элементарной геометрии
базис, состоящий из единичных
взаимно-перпендикулярных векторов. Для
простоты, также, ограничимся случаем
плоскости.
Пусть
![]() ,
,![]() .
Тогда
.
Тогда![]() и
и![]() элементы геометрической модели и для
них определена сумма
элементы геометрической модели и для
них определена сумма
![]() .
.
Учитываем,
что
![]() ,
,![]() ,
,![]() и
и![]() также элементы геометрической модели
и, используя свойства 1-4 сложения и
свойства 1-4 умножения, получаем:
также элементы геометрической модели
и, используя свойства 1-4 сложения и
свойства 1-4 умножения, получаем:
![]()
![]()
Согласно
соответствию (1), установленному выше,
заключаем, что
![]() – координаты вектора
– координаты вектора![]() .
Аналогично показывается, что вектор
.
Аналогично показывается, что вектор![]() имеет координаты
имеет координаты![]() .
.
Используя теорему Пифагора, находим длину вектора на плоскости
![]()
и в пространстве
![]() .
.
Наконец,
для противоположного вектора
![]() находим координаты:
находим координаты:![]() .
.
Вывод 2.
Координаты
![]() вектора
вектора![]() определяют
его длину и направление. В координатной
форме определены операции сложения
векторов и умножение векторов на число.
Доказательство этих фактов требует в
точности 8 свойств сложения и умножения,
доказанных в геометрической модели.
Поэтому эти 8 свойств называют аксиомами
модели векторного пространства.
определяют
его длину и направление. В координатной
форме определены операции сложения
векторов и умножение векторов на число.
Доказательство этих фактов требует в
точности 8 свойств сложения и умножения,
доказанных в геометрической модели.
Поэтому эти 8 свойств называют аксиомами
модели векторного пространства.
Мы завершили решение сформулированной в начале параграфа задачи А. Вот это решение:
На множестве направленных отрезков система восьми свойств операции сложения направленных отрезков и умножения на число определяет арифметическую модель векторного пространства.
Попутно мы устанавливаем следующее свойство.
Вывод 3.
Между элементами геометрической модели векторного пространства и элементами арифметической модели векторного пространства существует взаимнооднозначное соответствие (1), обозначим его
![]() ,
,
![]() .
(2)
.
(2)
Это соответствие сохраняет результат линейных операций сложения векторов и умножения на число:
![]() (3)
(3)
и называется изоморфизмом арифметической и геометрической моделей векторного пространства.
Абстрактное векторное пространство.
Восемь свойств сложения и умножения, установленных в геометрической модели, позволяют построить арифметическую модель и называются аксиомами векторного пространства.
Рассмотрим примеры моделей, удовлетворяющих этим аксиомам.
Пример 1.
Множество
многочленов степени не выше
![]()
![]()
образует
векторное пространство, в котором мономы
![]() –
базисные элементы, а коэффициенты
многочлена
–
базисные элементы, а коэффициенты
многочлена![]() –
координаты вектора
–
координаты вектора![]() в
этом базисе.
в
этом базисе.
Пример 2.
Пусть
![]() ,
,![]() ,…,
,…,![]() - «
- «![]() -местные
наборы»,
-местные
наборы»,![]() имеет 1 на
имеет 1 на![]() -м
месте и нули на остальных местах,
-м
месте и нули на остальных местах,![]() .
Тогда объекты
.
Тогда объекты
![]()
образуют
векторное пространство с базисными
элементами
![]() .
Обозначим это пространство
.
Обозначим это пространство![]() .
.
Векторное
пространство
![]() ,
позволяет определить размерность
всякого векторного пространства
,
позволяет определить размерность
всякого векторного пространства![]() при
помощи следующей аксиомы.
при
помощи следующей аксиомы.
9.
Аксиома размерности. Существует
изоморфизм
![]() .
.
Определение абстрактного векторного пространства.
Пусть
для элементов
![]() множества
множества![]() выполняется 8 аксиом векторного
пространства и аксиома размерности.
Тогда
выполняется 8 аксиом векторного
пространства и аксиома размерности.
Тогда![]() есть
есть![]() -мерное
абстрактное векторное пространство, а
-мерное
абстрактное векторное пространство, а![]() является его арифметической моделью.
является его арифметической моделью.
Элементы
множества
![]() могут быть произвольной природы.
Например:
могут быть произвольной природы.
Например:
выборки
 измерений
измерений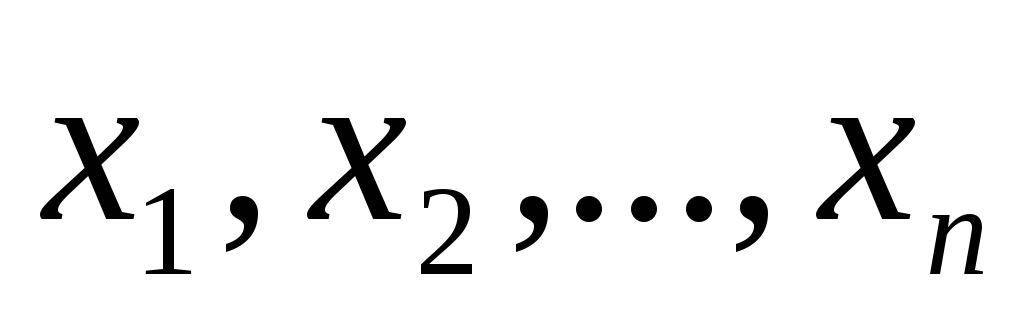 ;
;цены
 наименований
наименований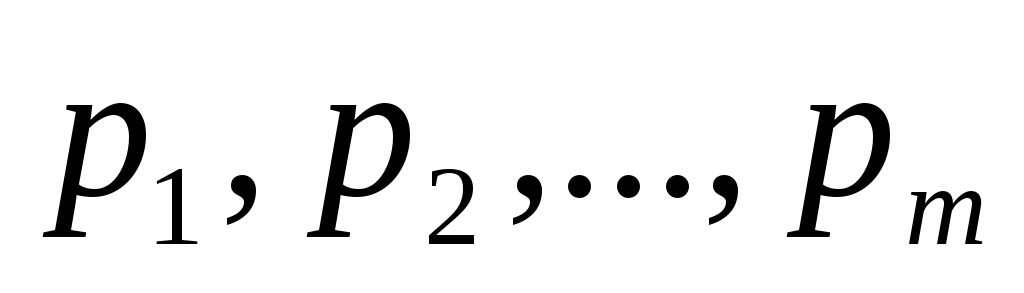 ;
;наборы продуктов, расстояния между заводом изготовителем и сырьевыми складами и т.д.
Следствие.
Все
![]() -мерные
векторные пространства имеют одну и ту
же арифметическую модель, поэтому
изоморфны.
-мерные
векторные пространства имеют одну и ту
же арифметическую модель, поэтому
изоморфны.
Множество
многочленов степени не выше
![]() в примере 1 образуют
в примере 1 образуют![]() -мерное
пространство. Изоморфизм, устанавливающий
размерность, задается в этом случае так
-мерное
пространство. Изоморфизм, устанавливающий
размерность, задается в этом случае так
![]() ,
,
![]() .
.
Здесь
![]() – мономы, а
– мономы, а![]() – базисные орты в
– базисные орты в![]() .
.
Если
векторное пространство
![]() содержит для всякого
содержит для всякого![]() подмножество,
подмножество,![]() ,
которое само является векторным
пространством и для него выполняется
аксиома размерности с заданным
,
которое само является векторным
пространством и для него выполняется
аксиома размерности с заданным![]() ,
то
,
то![]() назовем
бесконечным векторным пространством.
Примером такого пространства является
множество всех многочленов. Подмножества
многочленов степени не выше
назовем
бесконечным векторным пространством.
Примером такого пространства является
множество всех многочленов. Подмножества
многочленов степени не выше![]() образуют
образуют![]() -мерные
подпространства в этом пространстве.
-мерные
подпространства в этом пространстве.
