- •2. Классификация кинематических пар по связям.
- •3.Кинематические цепи и их структурные формулы.
- •4.Степень подвижности механизмов. Пассивные и активные звенья.
- •5.Основной принцип образования механизмов. Заменяющие механизмы.
- •7. Метод определения класса механизмов.
- •8.Аналитический метод исследования кинематики механизмов.
- •9. Графический метод определения кинематических параметров. План скоростей.
- •10. Порядок опр-я ускорений в многозвенных мех-ах. Т-ма подобия.
- •11.Виды трения. Коэф-фициенты трения покоя.
- •12. Основные характеристики сухого трения. Характеристика трения.
- •13. Трения в поступательных кинематических парах. Конус трения.
- •14.Трения качения без скольжения и проворачивания. Коэффициент трения качения.
- •15.Задачи силового исследования. Силы инерции. Точка качания.
- •16.Определение точки приложения результирующей силы инерции.
- •17.Реакции в кинематических парах. Статическая определимость кинематических цепей.
- •18.Последовательность проведения силового исследования механизмов.
- •19.Силовой расчет ведущего звена. Обоснование метода «рычага» Жуковского.
- •20.Задачи динамического исследования. Режимы движения механизмов. Уравнение энергетического баланса.
- •21.Коэффициент полезного действия. Определение кпд в последовательном соединении механизмов.
- •22.Приведенные силы и моменты сил. Определение их методом Жуковского.
- •23.Приведенная масса и приведенный момент инерции. Их определение.
- •24.Вывод уравнения движения механизма. Возможное аналитическое решение.
- •25.Графический метод решения уравнения движения механизма.
- •26.Неравномерное движение механизма. Коэффициент неравномерности. Определение момента инерции маховика.
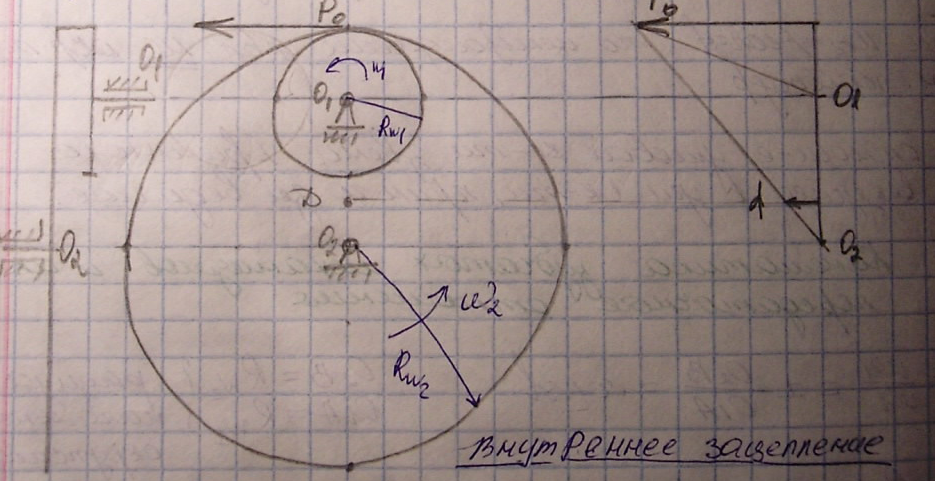
- •27. Зубчатые механизмы. Основная теорема зацепления и выводы.
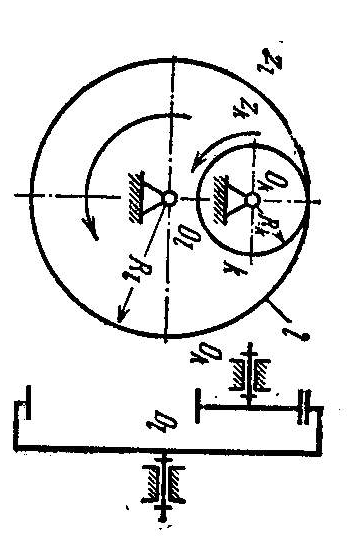
- •28. Передаточное отношение. Вывод формул для определения предаточных отношений в многозвенных механизмах.
- •29. Дифференциальные и планетарные мех-мы.
- •30.Эвольвента и её свойства. Вывод уравнения эвольвенты.
- •31.Проектирование эвольвентных профилей при внешнем зацеплении колес.
- •32.Дуга зацепления. Коэффициент перекрытия.
- •33.Методы нарезания зубчатых колес.
- •34.Подрезание зубьев. Обоснование его появления.
- •35. Определение коэффициента коррекции. Получение формулы.
- •36.Определение толщины зуба по делительной окружности коррегрованных колес. Получение формулы.
- •37.Определение угла сборки в зацеплении коррегрованных колес. Вывод формулы. Определение параметров зацепления коррегрованных колес. Получение формул.
- •38. Косозубые передачи. Шевронные колеса, их достоинства.
- •39.Конические зубчатые зацепления. Проектирование. Характеристика.
- •40.Гиперболойдные колеса. Получение гипоидных и винтовых механизмов. Червячное зацепление.
- •41.Проектирование рычажных механизмов по заданным положениям звеньев.
- •42. Доказательство условия проворачиваемости звеньев (теорема Грасгофа).
- •43. Проектирование кривошипно-коромыслового механизма по заданному коэффициенту изменения средней скорости коромысла.
- •44. Кулачковые механизмы. Угол давления. Жесткие и мягкие ударыв кулачковых механизмах.
- •45. Безударные законы движения толкателя. Минимальный радиус кулачка
28. Передаточное отношение. Вывод формул для определения предаточных отношений в многозвенных механизмах.
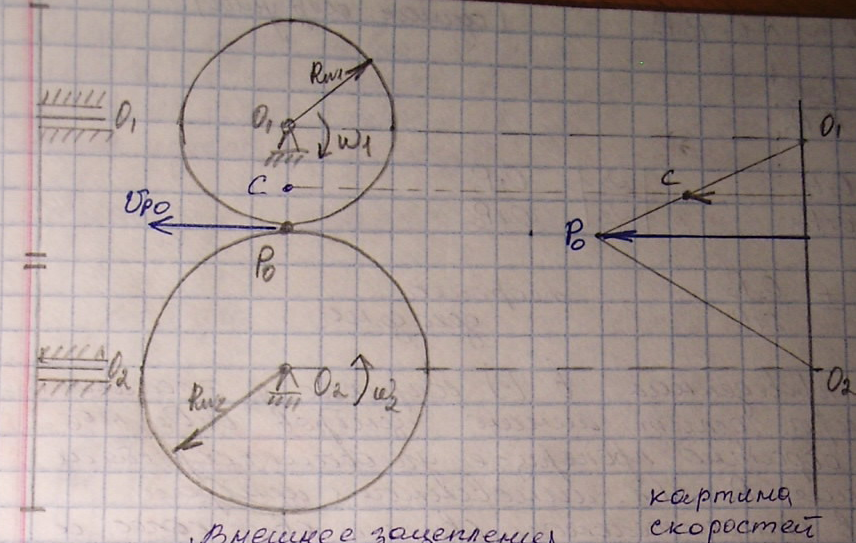
Передаточное отношение – отношение угловой скорости звена принятого за ведущее к угловой скорости звена принятого за ведомое.
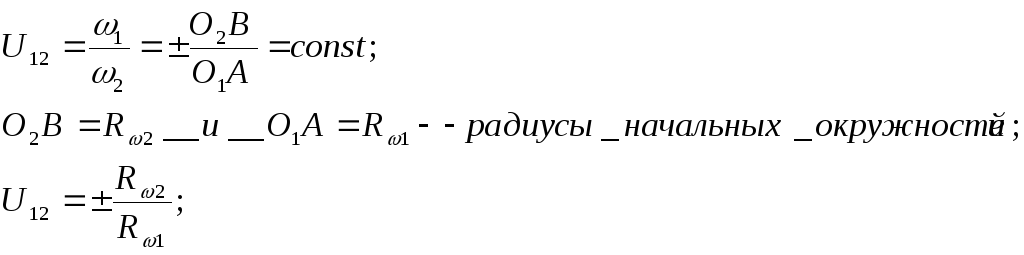
Рисунок из лекции 10
Для внешнего зацепления передаточные отношения отрицательны.
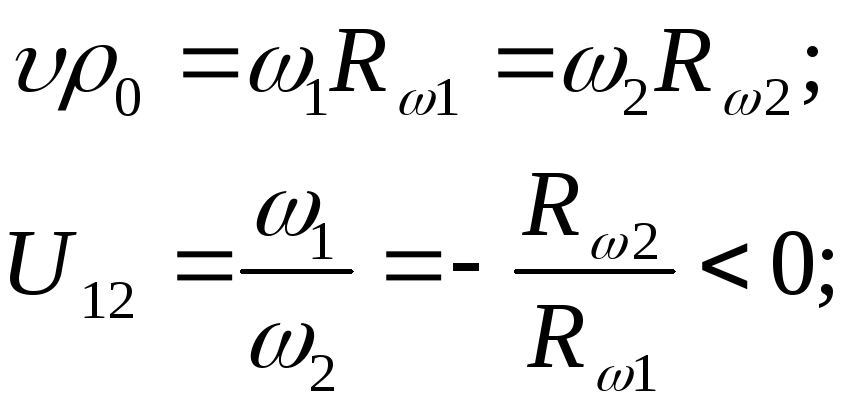


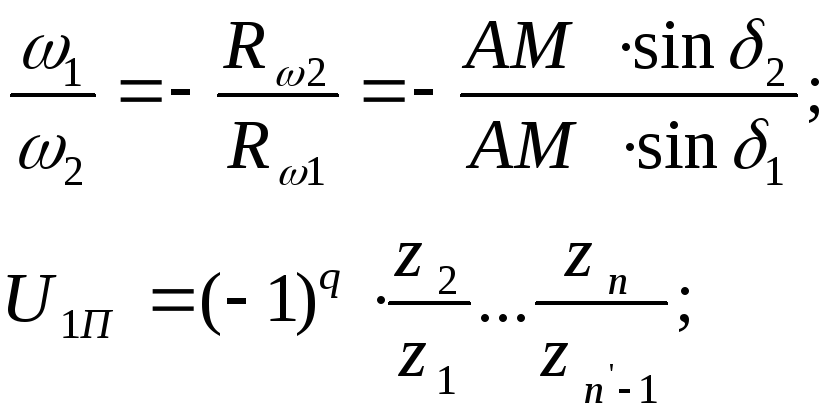 q
– число внешних зацеплений.
q
– число внешних зацеплений.
Передаточное отношение может быть определено ч/з число зубьев колес.
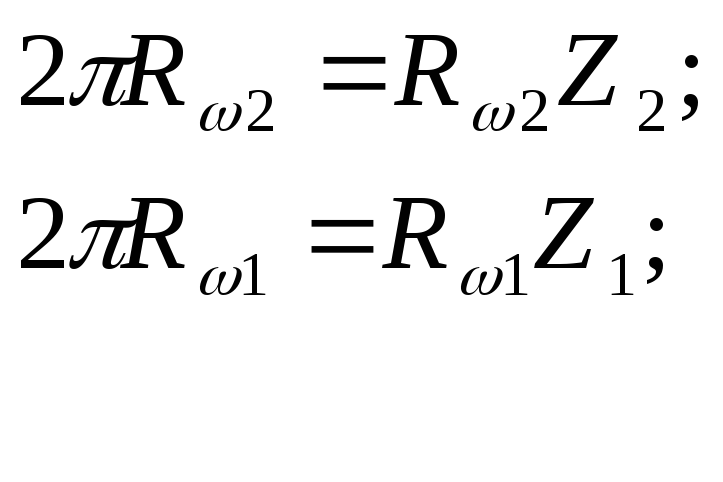
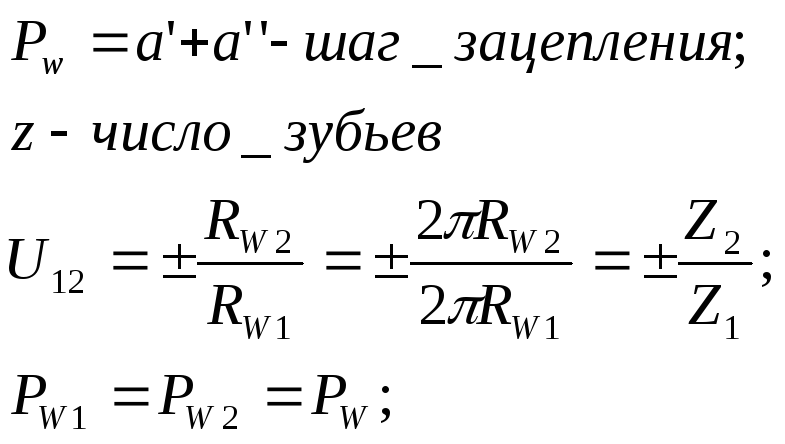
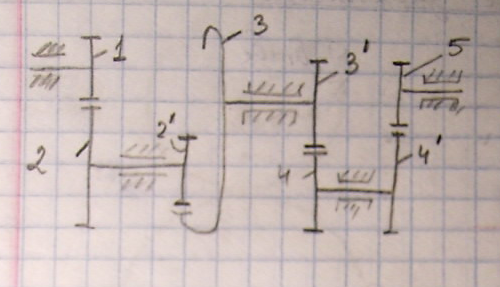
Определение передаточных отношений в многозвенных механизмах.
По определению
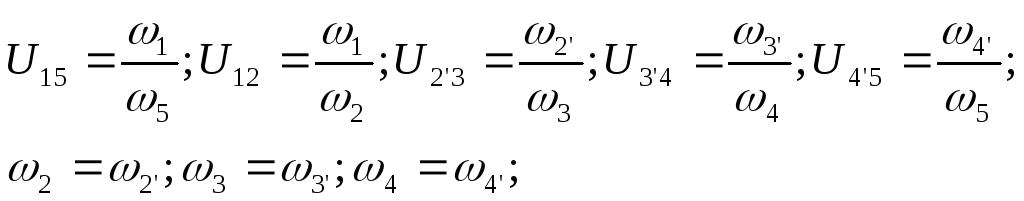
Для того, чтобы определить передаточное отношение в многозв. механизмах, необходимо получить фор-лу по которым оно определяется.
![]() те
передаточное отношение многозвенной
передачи = произведению передаточных
отношений каждого зацепления в этой
передаче.
те
передаточное отношение многозвенной
передачи = произведению передаточных
отношений каждого зацепления в этой
передаче.
![]() ,
где q-
число внешних зацеплений.
,
где q-
число внешних зацеплений.
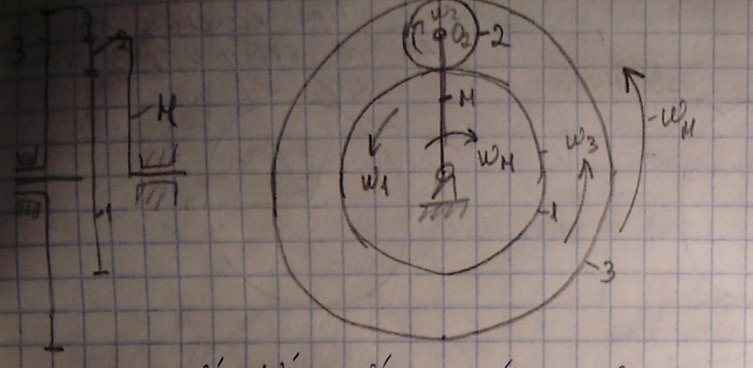
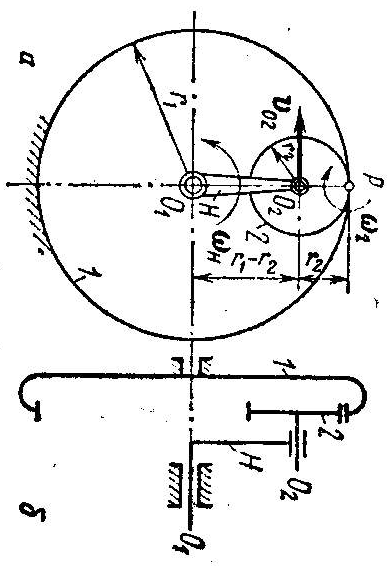
29. Дифференциальные и планетарные мех-мы.
Механизмы имеющие подвижные оси используются для того, чтобы при небольших габаритах получать большие передаточные отношения или решать определенные математические задачи. Среди этих мех-овимеются диф-ый и планетарные механизмы.
Если степень подвижности = 2 и более –дифференциальные механизмы => 2 и более ведущих звеньев .
1 ведущее звено – планетарные мех-мы.
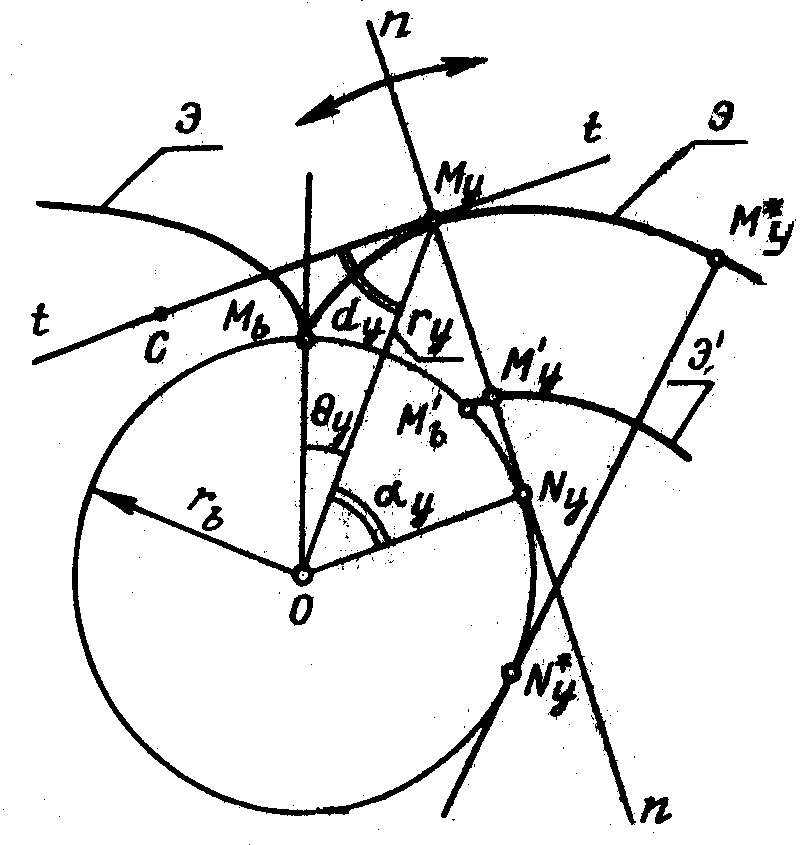
30.Эвольвента и её свойства. Вывод уравнения эвольвенты.
Геометрическое
место центров кривизны к-л кривой наз-ся
эволютой, а сама кривая по отношению к
эволюте наз-ся разверткой или эвольвентой.
Проведем окружность радиусом
![]() называемую основной, далее проведем к
ней касательно производящую прямуюnn
и покатим её по окружности без скольжения
сначала по часовой стрелке, а затем
против. Любая точка прямой, например,
точка M
называемую основной, далее проведем к
ней касательно производящую прямуюnn
и покатим её по окружности без скольжения
сначала по часовой стрелке, а затем
против. Любая точка прямой, например,
точка M![]() опишет при этом кривую Э, называемую
эвольвентой. Как видно из рисунка
эвольвента имеет две симметричные ветви
и точку возврата
опишет при этом кривую Э, называемую
эвольвентой. Как видно из рисунка
эвольвента имеет две симметричные ветви
и точку возврата
![]() ,
находящуюся на основной окружности.
,
находящуюся на основной окружности.
Свойства эвольвенты:
1.Нормаль к эвольвенте есть производящая
прямая nn,
т.е. нормаль к эвольвенте касательна к
основной окружности. 2.При увеличении
радиуса
![]() основной окружности эвольвента постепенно
теряет свою кривизну; в пределе при
основной окружности эвольвента постепенно
теряет свою кривизну; в пределе при![]() →
→![]() эвольвента превращается в прямую линию.
3.Радиус кривизны
эвольвента превращается в прямую линию.
3.Радиус кривизны![]() эвольвенты в текущей точкеM
эвольвенты в текущей точкеM![]() равен отрезку
равен отрезку
![]()
![]() .
Отсюда следует, что в точке
.
Отсюда следует, что в точке![]() ,
более удаленной от точки
,
более удаленной от точки![]() ,
чем тока
,
чем тока![]() ,
радиус кривизны
,
радиус кривизны![]() =
=![]() больше, чем радиус кривизны
больше, чем радиус кривизны![]() =
=![]() .
.
Укажем полярные
координаты точки
![]() :
полярный угол
:
полярный угол![]() и полярный радиус-вектор
и полярный радиус-вектор![]() (отрезок
(отрезок![]() ),
и профильный угол
),
и профильный угол![]() С,
обозначаемый
С,
обозначаемый![]() .
Составим уравнение эвольвенты, т.е.
установим аналитическую связь между
координатами
.
Составим уравнение эвольвенты, т.е.
установим аналитическую связь между
координатами![]() ,
,![]() ,
,![]() .
.
Т.к. прямая nn
катится по основной окружности без
скольжения, то отрезок
![]()
![]() равен дуге
равен дуге![]() :
:![]() =
=![]() .
Из первого свойства эвольвенты следует,
что угол
.
Из первого свойства эвольвенты следует,
что угол![]() равен углу
равен углу![]() =
=![]() .
Поэтому
.
Поэтому![]() =
=![]() ,
а
,
а![]() =
=![]() (
(![]() +
+![]() ).
Получим
).
Получим![]() =
=![]() +
+![]() ,
откуда :
,
откуда :![]() =
=![]() -
-![]() (1). Из ∆
(1). Из ∆![]() имеем:
имеем:![]() =
=![]() /
/![]() (2). Исключив из системы уравнений (1)-(2)
(2). Исключив из системы уравнений (1)-(2)
![]() ,
получим связь между
,
получим связь между![]() и
и![]() .
Т.о., система уравнений (1)-(2) – уравнение
эвольвенты в параметрической форме.
Из уравнения (1) видно, что
.
Т.о., система уравнений (1)-(2) – уравнение
эвольвенты в параметрической форме.
Из уравнения (1) видно, что![]() =ƒ(
=ƒ(![]() ).
Эта зависимость наз-ся эвольвентной и
записывается:
).
Эта зависимость наз-ся эвольвентной и
записывается:![]() =
=![]()
![]() .
.
Если взять на
производящей прямой nn
другую точку, например,
![]() и покатить прямуюnn
по основной окружности без скольжения,
то точка
и покатить прямуюnn
по основной окружности без скольжения,
то точка
![]() опишет эвольвенту
опишет эвольвенту![]() ,
такую же, как и эвольвента Э, но сдвинутую
относительно неё и
,
такую же, как и эвольвента Э, но сдвинутую
относительно неё и![]() =
=![]() .
.