Лекция 2. Линии второго порядка, заданные каноническими уравнениями.

§ 102. Эллипс и его каноническое уравнение

Эллипсом называется геометрическое место точек, для каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное число 2а, большее, чем расстояние 2с между фокусами.

Пусть М – произвольная точка эллипса, а и- его фокусы. Отрезкиитак же, как и длины этих отрезков, называются фокальными радиусами точкиМ эллипса. В силу данного определения эллипса (см. рис.1)

(1)

Из определения эллипса вытекает следующий способ его вычерчивания. Воткнем в чертежную доску две булавки и накинем на них замкнутую нить, длина которой равна . Натянем нить карандашом и будем передвигать его, держа нить все время натянутой. Карандаш опишет эллипс, так как суммарасстояний от острияМ карандаша до точек и, в которые воткнуты булавки, во время движения острия карандаша по бумаге не будет изменяться, оставаясь равной.

Введем на плоскости прямоугольную систему координат, принимая середину отрезка за начало координат, а за осьОх прямую , ориентированную от точкик точке. В выбранной системе координат фокусбудет иметь координаты (с, 0), а фокус - координаты (-с, 0). Обозначая координаты точки М эллипса через х и у, будем иметь

и соотношении (1) принимает вид:,

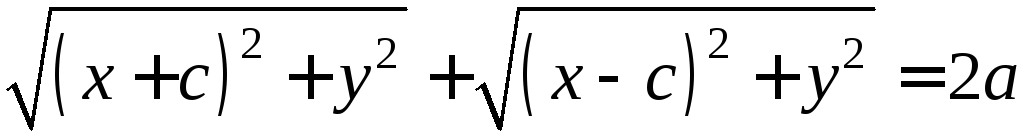или . (2)

Возводя обе части (2) в квадрат, получим

или .

Возводя обе части этого уравнения в квадрат, получим

,

или .

Так как по условию , то. Обозначаячерез

, (3)

получим

или . (4)

Мы доказали, что координаты любой токи М(х,у) эллипса удовлетворяют уравнению (4). Однако уравнение (4) еще нельзя назвать уравнением эллипса, так как не доказано обратное предложение, а именно: если числа х и у удовлетворяют уравнению (4), то точка М с координатами х и у удовлетворяет соотношению , т.е. лежит на эллипсе.

Докажем это. Пусть координаты точки М(х,у) удовлетворяют уравнению (4). Тогда

и, аналогично, .

Далее, поскольку

то , а так кактоиследовательно,

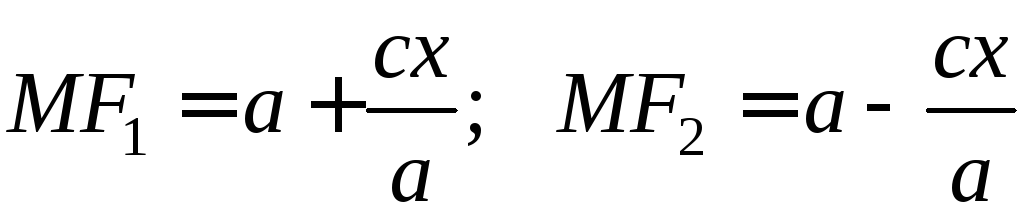, (5)

откуда .

Таким образом, (4) есть уравнение эллипса, так как доказано, что координаты любой точки М эллипса, т. е. любой точки, для которой

,

удовлетворяют уравнению (4), и, обратно, если два числа х и у удовлетворяют уравнению (4), то точка М с этими координатами х и у удовлетворяет соотношению ,

т. е. лежит на эллипсе.

Уравнение

называется каноническим уравнение эллипса.

§ 103. Исследование формы эллипса

Так как в каноническое уравнение эллипса координаты х и у входят в четной степени (именно во второй), то если на эллипсе

(1)

лежит точка М(х,у), т. е. координаты этой точки удовлетворяют уравнению (1), то на том же эллипсе лежат точки и, симметричные с точкойМ относительно осей Ох и Оу, и точка , симметричная с точкойМ относительно начала координат. Поэтому оси координат Ох и Оу для

эллипса, заданного каноническим уравнением (1) являются осями симметрии, а начало координат – центром симметрии. Из уравнения эллипсаследует, что для координат любой его точки имеют место соотношения

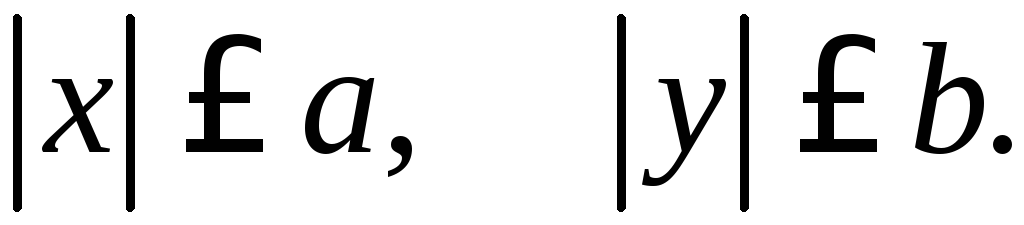
Геометрически это значит, что эллипс расположен внутри прямоугольника, сторонами которого являются прямые

Точки пересечения эллипса с его осями симметрии называются вершинами эллипса. Таким образом, эллипс (1) имеет 4 вершины: ,,,.

Полуосью эллипса называется отрезок (а также длина этого отрезка), одним концом которого является центр симметрии эллипса, а другим – одна из его вершин; а называется большей полуосью эллипса, а b – меньшей полуосью.

Отрезок - большая ось эллипса.

Отрезок - меньшая ось эллипса.

Замкнутая линия является выпуклой, если любая прямая пересекает ее не более чем в двух точках. Эллипс есть выпуклая замкнутая линия, так как, решая уравнение (1) эллипса совместно с уравнением прямой или, получим уравнение второй степени относительнох или у, значит, любая прямая пересекает эллипс не более чем в двух точках.

Итак, эллипс – замкнутая выпуклая линия, имеющая центр симметрии и две (взаимно перпендикулярные) оси симметрии.

Условимся уравнение называть каноническим уравнением эллипса и в том случае, когдаа = b и когда a < b.

В случае а = b уравнение примет вид

,

т.е. является уравнением окружности радиуса а с центром в начале координат. Таким образом, мы рассматриваем окружность как частный случай эллипса. Этот частный случай соответствует совпадению фокусов ис центром окружности.

В случае а < b большей полуосью будет b, а меньшей - а. Фокусы будут расположены на оси Оу на расстоянии от центра эллипса.

Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:

Так как тот. е. эксцентриситет эллипса есть неотрицательное число, меньшее единицы.

Отметим, что (поскольку).

Следовательно, эксцентриситет определяется отношением полуосей эллипса, и, обратно, отношение полуосей эллипса определяет его эксцентриситет.

Если эксцентриситет равен нулю е = 0, то а = b и эллипс является окружностью. Чем ближе эксцентриситет е к 1, тем меньше и, значит, тем меньше отношение меньшей полуоси к большей. Таким образом, эксцентриситет характеризует степень «вытянутости» эллипса.

Вспоминая формулы: