
- •Часть 1. Физические основы механики
- •Введение
- •Глава I. Кинематика
- •§1. Перемещение точки. Векторы и скаляры
- •§2. Некоторые сведения о векторах
- •§3. Скорость
- •§4. Вычисление пройденного пути
- •§5. Равномерное движение
- •§6. Проекции вектора скорости на координатные оси
- •§7. Ускорение
- •§8. Прямолинейное равнопеременное движение
- •§9. Ускорение при криволинейном движении
- •§10. Кинематика вращательного движения
- •§11. Связь между векторами v и ω
- •Глава II. Динамика материальной точки
- •§12. Классическая механика. Границы ее применимости
- •§13. Первый закон Ньютона. Инерциальные системы отсчета
- •§14. Второй закон Ньютона
- •§15. Единицы измерения и размерности физических величин
- •§16. Третий закон Ньютона
- •§17. Принцип относительности Галилея
- •§18. Сила тяжести и вес
- •§19. Силы трения
- •§20. Силы, действующие при криволинейном движении
- •§21. Практическое применение законов Ньютона
- •§22. Импульс
- •§23. Закон сохранения импульса
- •Глава III. Работа и энергия
- •§24. Работа
- •§25. Мощность
- •§26. Потенциальное поле сил. Силы консервативные и неконсервативные
- •§27. Энергия. Закон сохранения энергии
- •§28. Связь между потенциальной энергией и силой
- •§29. Условия равновесия механической системы
- •§30. Центральный удар шаров
- •Глава IV. Неинерциальные системы отсчета
- •§31. Силы инерции
- •§32. Центробежная сила инерции
- •§33. Сила Кориолиса
- •Глава V. Механика твердого тела
- •§34. Движение твердого тела
- •§35. Движение центра инерции твердого тела
- •§36. Вращение твердого тела. Момент силы
- •§37. Момент импульса материальной точки» Закон сохранения момента импульса
- •§38 Основное уравнение динамики вращательного движения
- •§39. Момент инерции
- •§40. Кинетическая энергия твердого тела.
- •§41. Применение законов динамики твердого тела
- •§42. Свободные оси. Главные оси инерции
- •§43 Момент импульса твердого тела
- •§44. Гироскопы
- •§45. Деформации твердого тела
- •Глава VI. Всемирное тяготение
- •§46. Закон всемирного тяготения
- •§47. Зависимость ускорения силы тяжести от широты местности
- •§48. Масса инертная и масса гравитационная
- •§49. Законы Кеплера
- •§50. Космические скорости
- •Глава VII. Статика жидкостей и газов
- •§51. Давление
- •§52. Распределение давления в покоящихся жидкости и газе
- •§53. Выталкивающая сила
- •Глава VIII. Гидродинамика
- •§54. Линии и трубки тока. Неразрывность струи
- •§55. Уравнение Бернулли
- •§56. Измерение давления в текущей жидкости
- •§57. Применение к движению жидкости закона сохранения импульса
- •§58. Силы внутреннего трения
- •§59. Ламинарное и турбулентное течение
- •§60. Движение тел в жидкостях и газах
- •Часть 2. Колебания и волны
- •Глава IX. Колебательное движение
- •§61. Общие сведения о колебаниях
- •§62. Гармонические колебания
- •§63. Энергия гармонического колебания
- •§64. Гармоническим осциллятор Систему, описываемую уравнением
- •§65. Малые колебания системы вблизи положения равновесия
- •§66. Математический маятник
- •§67. Физический маятник
- •§68. Графическое изображение гармонических колебаний. Векторная диаграмма
- •§69. Сложение колебаний одинакового направления
- •§70. Биения
- •§71. Сложение взаимно перпендикулярных колебаний
- •§72. Фигуры Лиссажу
- •§73. Затухающие колебания
- •§74. Автоколебания
- •§75. Вынужденные колебания
- •§76. Параметрический резонанс
- •Глава X. Волны
- •§77. Распространение волн в упругой среде
- •§78. Уравнения плоской и сферической волн
- •§79. Уравнение плоской волны, распространяющейся в произвольном направлении
- •§80. Волновое уравнение
- •§81 Скорость распространения упругих волн
- •§82. Энергия упругой волны
- •§83. Интерференция и дифракция воли
- •§84. Стоячие волны
- •§85. Колебания струны
- •§86. Эффект Допплера
- •§87. Звуковые волны
- •§88. Скорость звуковых волн в газах
- •§89. Шкала уровней силы звука
- •§90. Ультразвук
- •Часть 3. Молекулярная физика и термодинамика
- •Глава ХI. Предварительные сведения
- •§91. Молекулярно-кинетическая теория (статистика) и термодинамика
- •§92. Масса и размеры молекул
- •§93. Состояние системы. Процесс
- •§94. Внутренняя энергия системы
- •§95. Первое начало термодинамики
- •§96. Работа, совершаемая телом при изменениях его объема
- •§97. Температура
- •§98. Уравнение состояния идеального газа
- •Глава XII. Элементарная кинетическая теория газов
- •§99. Уравнение кинетической теории газов для давлений
- •§100. Строгий учет распределения скоростей молекул по направлениям
- •§101. Равнораспределение энергии по степеням свободы
- •§102. Внутренняя энергия и теплоемкость идеального газа
- •§103. Уравнение адиабаты идеального газа
- •§104. Политропические процессы
- •§105. Работа, совершаемая идеальным газом при различных процессах
- •§106. Распределение молекул газа по скоростям
- •§107. Экспериментальная проверка закона распределения Максвелла
- •§108. Барометрическая формула
- •§109. Распределение Больцмана
- •§110. Определение Перреном числа Авогадро
- •§111. Средняя длина свободного пробега
- •§112. Явления переноса. Вязкость газов
- •§113. Теплопроводность газов
- •§114. Диффузия & газах
- •§115. Ультраразреженные газы
- •§116. Эффузия
- •Глава ХIII. Реальные газы
- •§117. Отклонение газов от идеальности
- •§118. Уравнение Ван-дер-Ваальса
- •§119. Экспериментальные изотермы
- •§120. Пересыщенный пар и перегретая жидкость
- •§121. Внутренняя энергия реального газа
- •§122. Эффект Джоуля-Томсона
- •§123. Ожижение газов
- •Глава XIV. Основы термодинамики
- •§124. Введение
- •§125. Коэффициент полезного действия тепловой машины
- •§126. Второе начало термодинамики
- •§127. Цикл Карно
- •§128. Коэффициент полезного действия обратимых и необратимых машин
- •§129. К.п.д. цикла Карно для идеального газа
- •§130. Термодинамическая шкала температур
- •§131. Приведенное количество тепла. Неравенство Клаузиуса
- •§132. Энтропия
- •§133. Свойства энтропии
- •§134. Теорема Нернста
- •§135. Энтропия и вероятность
- •§136. Энтропия идеального газа
- •Глава XV. Кристаллическое состояние
- •§137. Отличительные черты кристаллического состояния
- •§138. Классификация кристаллов
- •§139. Физические типы кристаллических решеток
- •§140. Тепловое движение в кристаллах
- •§141. Теплоемкость кристаллов
- •Глава XVI. Жидкое состояние
- •§142. Строение жидкостей
- •§143. Поверхностное натяжение
- •§144. Давление под изогнутой поверхностью жидкости
- •§145. Явления на границе жидкости и твердого тела
- •§146. Капиллярные явления
- •Глава XVII. Фазовые равновесия и превращения
- •§147. Введение
- •§148. Испарение и конденсация
- •§149. Плавление и кристаллизация
- •§150. Уравнение Клапейрона—Клаузиуса
- •§151. Тройная точка. Диаграмма состояния
- •Предметный указатель

ωn = υ2
R
Подставляя в это выражение υ из (10.9), находим, что
ωn = ω2R
Модуль тангенциального ускорения в соответствии с (9.8) равен
опять уравнением (10.9), получаем:
lim |
Δυ |
|
= |
|
lim |
(ωR) |
|
= |
|
lim R |
Δω |
|
= R |
|
lim |
Δω |
|
|
|
|
|
|
|||||||||||
t→0 |
t |
|
|
|
t→0 |
t |
|
|
|
t→0 |
t |
|
|
|
t→0 |
t |
т.е.
ωτ = βR
(10.10) ddtυ . Воспользовавшись
= Rβ,
(10.11)
Таким образом, как нормальное, так и тангенциальное ускорение растет линейно с R — расстоянием точки от оси вращения.
§11. Связь между векторами v и ω
Кроме рассмотренных ранее операций сложения и вычитания векторов, а также умножения вектора на скаляр (см. §2), существуют также операции перемножения векторов. Два вектора можно умножить друг на друга двумя способами: первый способ дает в результате некоторый новый вектор, второй — приводит к скалярной величине. Отметим, что операции деления вектора на вектор не существует.
Сейчас мы рассмотрим секторное произведение векторов. Скалярное произведение векторов мы введем позднее, когда оно нам понадобится.
Векторным произведением двух векторов А и В называется вектор С, обладающий следующими свойствами:
1) модуль вектора С равен произведению модулей перемножаемых векторов на синус угла α между ними (рис 35):
C=ABsinα
2) вектор С перпендикулярен к плоскости, в которой лежат векторы А и В, причем направление его связано с направлениями А и В по правилу правого винта: если смотреть вслед вектору С, го совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке.
Символически векторное произведение можно записать двумя способами: |AB| или A× B .
Мы будем пользоваться первым из этих способов, причем иногда для облегчения чтения формул будем ставить запятую между сомножителями. Не следует применять одновременно косой крест и квадратные скобки: [А× В], Недопустима запись такого вида: [АВ]=ABsinα. Слева здесь стоит вектор, справа — модуль этого вектора, т. е. скаляр. Справедливо следующее равенство:
| [AB]|= ABsin α. |
(11.1) |
Поскольку направление векторного произведения определяется направлением вращения от первого сомножителя ко второму, результат векторного перемножения двух векторов зависит от порядка сомножителей. Изменение порядка сомножителей вызывает изменение направления результирующего вектора на противоположное (рис. 35)
[BA] = − [AB]
или
B× A = −(A × B).
33
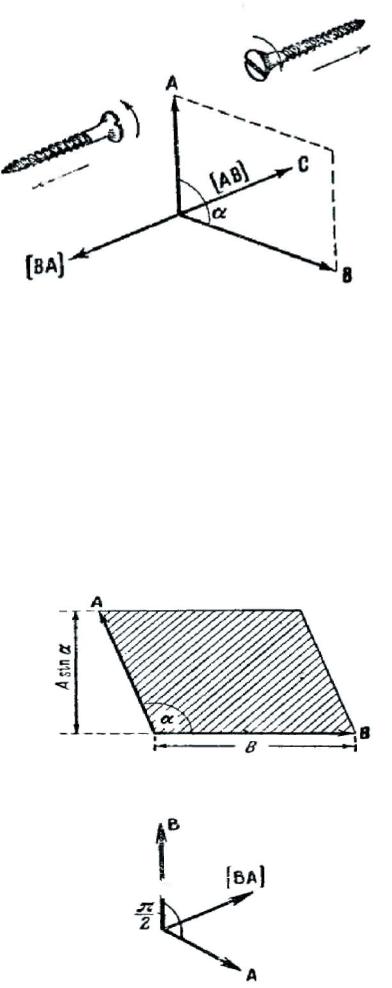
Рис. 35.
Таким образом, векторное произведение не обладает свойством коммутативности. Можно доказать, что векторное произведение дистрибутивно, т. е. что
[A,(B1 + B2 + ...+ BN )] = [AB1 ]+ [AB2 ]+ ...+ [ABN ]. |
(11.2) |
Векторное произведение двух полярных или двух аксиальных векторов есть аксиальный вектор. Векторное произведение аксиального вектора на полярный (или наоборот) будет, однако, вектором полярным. Изменение условия, определяющего направление аксиальных векторов, на обратное приведет в этом случае к изменению знака перед векторным произведением и одновременно к изменению знака перед одним из сомножителей, В итоге величина, выражаемая векторным произведением остается без изменений.
Модулю векторного произведения можно дать простую геометрическую интерпретацию: выражение ABsinα численно равно площади параллелограмма, построенного на векторах А и В (рис. 36; вектор С=[АВ] направлен в этом случае перпендикулярно к плоскости чертежа, за чертеж).
Рис 36.
Пусть векторы А и В взаимно перпендикулярны (рис. 37).
34
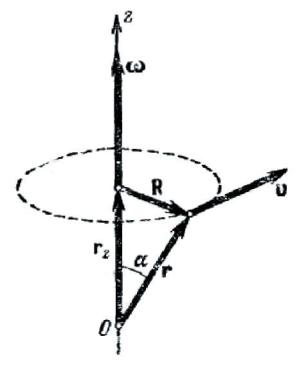
Рис. 37.
Образуем двойное векторное произведение этих векторов:
D= A,[BA] ,
т. е. умножим вектор В на А, а затем умножим вектор А на вектор, получившийся в результате первого умножения. Вектор [ВА] имеет модуль, равный BA(sin α = sin π2
векторами А и B углы, равные π/2. Следовательно, модуль вектора D равен |A|*|[BA]|=A*BA=A2B. Направление же вектора D, как легко видеть из рис. 37, совпадает с направлением вектора В. Это дает нам основание написать следующее равенство:
A, |
BA |
= A2B. |
(11.3) |
|
|
[ |
] |
|
|
Рис. 38.
Формулой (11.3) мы будем в дальнейшем пользоваться неодноктратно. Подчеркнем, что она справедлива только в том случае, когда векторы А и В взаимно перпендикулярны.
Уравнение (10.9) устанавливает связь между модулями векторов v и ω. С помощью векторного произведения может быть написано выражение, дающее cooтношение между самими векторами. Пусть тело вращает вокруг оси z с угловой скоростью ω (рис. 38). Jleгко видеть, что векторное произведение ω на радиус-вектор точки, скорость v которой мы хотим найти, представляет собой вектор, совпадающий по направлению с вектором v и имеющий модуль, равный ωr sinα=ωR, т.е. v [см. формулу (10.9)]. Таким образом, векторное произведение [ωR] и по направлению и по модулю равно вектору v:
v=[ωr] |
(11.4) |
Формуле (11.4) можно придать иной вид. Для этого представим радиус-вектор r в виде суммы двух составляющих — вектора rz, параллельного оси z и вектора, перпендикулярного к оси z: r=rz+R (см. рис. 38). Подставив это выражение в формулу (11.4) и воспользовавшись дистрибутивностью векторного произведения [см. (11.2)], получим:
[ωr] = [ω(rz + R)] = [ωrz ]+ [ωR].
Векторы ω и rz коллинеарны. Поэтому их векторное произведение равно нулю (sinα=0). Следовательно, можно написать, что
v=[ωR] |
(11.5) |
35
