
AGLA
.pdf
її вершинi, що належить фокальнiй осi.
8.82.Елiпс при русi вздовж площини дотикається двох взаємно перпендикулярних прямих. Яку лiнiю описує центр елiпса?
8.83.Знайти геометричне мiсце точок, добуток вiдстаней вiд яких до бiчних сторiн рiвнобедреного трикутника дорiвнює квадрату вiдстанi до його основи.
8.84.Довести, що добуток вiдстанi вiд фокуса лiнiї другого порядку до двох паралельних дотичних до неї дорiвнює квадрату малої пiввiсi у випадку елiпса i квадрату уявної пiвосi у випадку гiперболи.
8.85.Довести, що пряма, яка з’єднує фокус F параболи з точкою перетину дотичних до параболи в двох довiльних її точках M1 i M2 дiлить навпiл кут M1F M2.
8.86.Знайти геометричне мiсце точок проекцiй фокусу
а) елiпса; |
б) гiперболи; |
в) параболи |
на всi прямi, якi дотикаються вiдповiдної кривої.
Полярнi рiвняння кривих другого порядку
8.87. Скласти полярне рiвняння елiпса, вважаючи, що напрям полярної осi збiгається з додатним напрямом осi абсцис, а полюс знаходиться в
(1) лiвому фокусi елiпса; |
(2) правому фокусi елiпса, |
якщо
151
|
x2 |
|
|
y2 |
|
x2 |
|
y2 |
|||||||
а) |
|
|
+ |
|
|
|
= 1; |
в) |
|
+ |
|
= 1; |
|||
|
|
9 |
|
81 |
|||||||||||
25 |
|
|
|
|
|
|
225 |
|
|
|
|||||
б) |
x2 |
|
|
|
|
y2 |
г) |
x2 |
|
y2 |
|||||
|
|
+ |
|
|
= 1; |
|
+ |
|
= 1. |
||||||
|
|
25 |
|
|
|||||||||||
169 |
|
|
400 |
|
144 |
||||||||||
8.88. Скласти полярне рiвняння кожної гiлки гiперболи, вважаючи, що напрям полярної осi збiгається з додатним напрямом осi абсцис, а полюс знаходиться в
|
|
|
|
|
|
|
|
(1) правому фокусi |
(2) лiвому фокусi |
|||||||
гiперболи, якщо |
|
|
|
|
|
|
|
|
||||||||
а) |
x2 |
y2 |
|
x2 |
y2 |
|||||||||||
|
− |
|
|
|
= 1; |
в) |
|
− |
|
|
= 1; |
|||||
16 |
|
9 |
36 |
64 |
||||||||||||
б) |
x2 |
|
|
y2 |
г) |
x2 |
|
y2 |
||||||||
|
− |
|
|
= 1; |
|
− |
|
= 1. |
||||||||
144 |
25 |
576 |
49 |
|||||||||||||
8.89. Скласти полярне рiвняння параболи, вважаючи, що напрям полярної осi збiгається з додатним напрямом осi абсцис, а полюс знаходиться в фокусi параболи, якщо
а) y2 = x; |
б) y2 = 4x; |
в) y2 = 5x; |
г) y2 = 10x. |
8.90. Визначити, якi лiнiї заданi наступними рiвняннями. Якщо крива є елiпсом або гiперболою, знайти її пiвосi, якщо параболою - знайти її параметр:
а) ρ = |
|
16 |
|
; |
в) ρ = |
|
16 |
; |
|
|
|
|
|
||||||
3 |
− 5 cos ϕ |
5 − 3 cos ϕ |
|
||||||
б) ρ = |
|
1 |
; |
|
г) ρ = − |
27 |
|
; |
|
|
|
|
|
||||||
1 |
− cos ϕ |
|
4 + 5 cos ϕ |
||||||
152

д) ρ = |
18 |
|
|
; |
ж) ρ = |
50 |
|
; |
|
|
|
||||||
5 + 4 cos ϕ |
13 − 12 cos ϕ |
|||||||
|
36 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
е) ρ = |
|
|
; |
з) ρ = |
2 − 2 cos ϕ; |
|
||
|
|
|
|
|||||
5 cos ϕ |
− |
4 |
|
|
||||
|
|
|
|
и) ρ = |
64 |
|
. |
|
|
4 |
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
15 + 17 cos ϕ |
||||
|
|
|
|
|
|
|
||
є) ρ = 1 − cos ϕ; |
|
|
|
|||||
|
|
|
|
|
||||
8.91.Через фокус параболи проведено всi можливi хорди. На кожнiй з них вiд фокуса в напрямку бiльш вiддаленого кiнця хорди вiдкладається вiдрiзок, який дорiвнює рiзницi вiдрiзкiв, на якi фокус дiлить хорду. Знайти геометричне мiсце кiнцiв цих вiдрiзкiв.
8.92.Довести, що сума обернених величин вiдрiзкiв, на якi фокус лiнiї другого порядку дiлить хорду, що проходить через цей фокус, є величина стала.
Зведення загального рiвняння кривої другого
порядку до канонiчного виду
8.93. Довести, що криву другого порядку, яка в деякiй системi координат задається рiвнянням
Ax2 + By2 + 2Cx + 2Dy + E = 0, A2 + B2 =6 0
за допомогою паралельного переносу можна звести до канонiчного виду. Вказати зв’язок мiж старою i новою системами координат. Дослiдити тип кривої в залежностi вiд значень параметрiв A, B, C, D, E.
8.94. Кожне з наступних рiвнянь звести до канонiчного виду, визначити який геометричний образ вони визначають, в кожному випадку зобразити на рисунку осi старої i нової систем координат, а також геометричний образ (якщо це можливо), який визначається цим рiвнянням:
153
а) 7x2 |
+ 7y2 + 6x − 2y = 10; |
е) 2x2 + y2 |
+ 4x − 6y + 11 = 0; |
|
б) 9x2 |
− 16y2 − 6x + 8y = 144; |
є) 2x2 + y2 |
+ 4x − 6y + 12 = 0; |
|
в) 9x2 + 4y2 + 6x − 4y = 2; |
ж) x2 − 5x + 11 = 0; |
|||
г) 12x2 − 12x − 32y = 29; |
з) 25x2 |
− 30x + 9 = 0; |
||
д) 9y2 − 7y = 16; |
и) 45x2 |
−36y2 −90x−24y + 41 = 0. |
||
8.95. Довести, що криву другого порядку, яка в деякiй системi координат задається рiвнянням
Ax2 + 2Bxy + Cy2 + D = 0, A2 + B2 + C2 =6 0
за допомогою повороту системи координат можна звести до канонiчного виду. Вказати зв’язок мiж старою i новою системами координат. Дослiдити тип кривої в залежностi вiд значень параметрiв A, B, C, D, E.
8.96. Кожне з наступних рiвнянь звести до канонiчного виду, визначити який геометричний образ вони визначають, в кожному випадку зобразити на рисунку осi старої i нової систем координат, а також геометричний образ (якщо це можливо), який визначається цим рiвнянням:
а) 2x2 |
+ 6xy + 10y2 − 121 = 0; |
д) x2 − 2xy + y2 + 2x + 2y = 0; |
|||||||||
б) 9xy + 4 = 0; |
е) 9x2 − 6xy + y2 − 10 = 0; |
||||||||||
в) 2x |
2 |
√ |
|
|
є) 81x |
2 |
− 36xy + 4y |
2 |
= 0; |
||
|
|||||||||||
|
− 2 3xy + 9 = 0; |
|
|
||||||||
г) 18x2 + 24xy + 11y2 − 3 = 0; |
ж) 3x2 − 4√ |
|
xy + 4y2 = 0. |
||||||||
5 |
|||||||||||
8.97. Довести, що крива другого порядку, яка в деякiй системi координат задається рiвнянням
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0, A2 + B2 + C2 =6 0
154
має центр симетрiї тодi i тiльки тодi, коли AC − B2 =6 0, причому координати центра симетрiї (x0, y0) задовольняють наступну систему
лiнiйних рiвнянь |
( Bx0 |
+ Cy0 |
+ E = 0. |
|
|||
|
Ax0 |
+ By0 |
+ D = 0, |
8.98. Кожне з наступних рiвнянь звести до канонiчного виду, визначити який геометричний образ вони визначають, в кожному випадку зобразити на рисунку осi старої i нової систем координат, а також геометричний образ (якщо це можливо), який визначається цим рiвнянням:
а) 2x2 − 4xy + 5y2 + 8x − 2y + 9 = 0;
б) 4xy − 3y2 − 4x + 10y − 6 = 0;
в) 9x2 − 24xy + 16y2 − 8x + 19y + 4 = 0;
г) x2 − xy + y2 + x + y = 0;
д) xy + 2x + y = 0;
е) x2 − 2xy + y2 − 10x − 6y + 25 = 0;
є) 5x2 + 12xy + 10y2 − 6x + 4y − 1 = 0;
ж) 8x2 + 34xy + 8y2 + 18x − 18y − 17 = 0;
з) 25x2 − 30xy + 9y2 + 68x + 19 = 0;
и) 8x2 + 6xy + 6x + 3y + 1 = 0;
i) 4x2 + 12xy + 9y2 − 8x − 12y − 5 = 0;
ї) 225x2 − 240xy + 64y2 + 30x − 16y + 1 = 0;
к) x2 + 2xy + y2 − 5x − 5y + 4 = 0;
л) 5x2 − 6xy + 5y2 + 2x − 14y + 13 = 0;
м) x2 − 2xy + y2 + 8x − 8y + 22 = 0;
155
н) 5x2 + 8xy + 5y2 − 10x − 8y + 41 = 0;
о) 15x2 − 16xy − 15y2 − 62x − 44y − 13 = 0.
8.99. Задано криву другого порядку γ, рiвняння якої в деякiй системi координат має вигляд
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0, |
|
|
A2 + B2 + C2 6= 0. |
||||||||||||||||||
Нехай |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 |
|
|
||||||||||||||||||
|
деякiй iншiй системi координат. Довести, що мають мiсце |
||||||||||||||||||||
рiвняння γ в |
e |
e |
ee |
e |
e |
|
|
e |
e |
|
|
e |
e |
|
|
e |
|
|
|
|
|
рiвностi |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
A + C = A + C, δ = |
A B |
= |
A B |
, |
|
|||||||||||||||
|
B C |
B C |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|||
|
|
e |
|
e |
|
|
|
|
|
|
|
|
|
|
e |
|
|
||||
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A B D |
|
|
|
|
B D |
|
e |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|||
|
|
= |
B C E |
= |
B C E |
|
|
|
|
|
|||||||||||
|
|
|
|
D E |
F |
|
|
|
|
e |
|
e |
|
e |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
D E |
|
F |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
e |
|
e |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
e |
A B D |
|
||||
|
|
|
|
|
|
|
A B e |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
є ортого- |
|
(тобто величини S = A + C, δ = |
B |
|
C |
, |
|
|
= |
B |
|
C |
E |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D E |
F |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нальними iнварiантами кривої другого порядку вони не змiнюються |
|||
|
|
|
|
|
|
|
|
при переходi вiд одної прямокутної декартової системи координат до |
|
|
|
iншої).
8.100. Довести, що крива другого порядку, яка в деякiй системi координат задається рiвнянням
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0, A2 + B2 + C2 =6 0,
а) є кривою елiптичного типу (елiпсом, виродженим елiпсом або уявним елiпсом), якщо δ > 0 (див. позначення δ в задачi 8.99);
156

б) є кривою гiперболiчного типу (гiперболою або парою перетинних прямих), якщо δ < 0;
в) є кривою параболiчного типу (параболою, парою паралельних прямих, парою уявних паралельних прямих або парою паралельних прямих, якi збiгаються), якщо δ = 0.
8.101. Задано криву другого порядку γ, рiвняння якої в деякiй системi координат має вигляд
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0, A2 + B2 + C2 =6 0.
Довести, що
а) коренi λ1 i λ2 характеристичного рiвняння λ2 −Sλ+δ = 0 є дiйсними i одночасно не обертаються в нуль (див. позначення S, δ в задачi 8.99);
б) нехай K = λ1 − A, тодi за допомогою замiни змiнних
|
|
|
|
|
|
|
|
|
|
|
√B2 |
+ K2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x = |
Bx − Ky |
|
, |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ke |
+ |
|
|
e |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
2 |
|
|
|
|
|
|
2 , |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
By |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
+ |
|
e |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
координат на кут α, де |
|
|
|
||||||||||||||||||||||
тобто повороту системи |
|
|
|
|
, якщо B > 0 |
|
|
|
|
||||||||||||||||||||||
|
α = arctg B |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
− |
arctg |
|
K |
, якщо B < 0, |
|
|
|
||||||||||||||||||
|
|
|
|
|
B |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зведено до вигляду |
|
|
|
|
|
|
|
|||||||||||||||||||
рiвняння γ може бути |
|
|
|
+ 2 e |
|
|
+ 2 e |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
де |
λ1x |
+ |
2 |
|
|
|
|
|
|
|
+ |
|
= 0 |
|
|
|
|||||||||||||||
|
|
2 |
|
|
λ y2 |
|
|
|
Dx |
|
|
|
|
Ey |
|
|
F |
|
, |
|
|
||||||||||
|
|
e |
|
|
+ e |
|
|
|
|
e |
|
|
|
|
|
|
|
e BK + BE |
|||||||||||||
D = |
|
BD |
|
EK |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
, |
|
|
|
E = |
|
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
e |
|
|
√B2 + K2 |
|
|
|
|
e |
|
|
|
|
|
√B2 |
+ K2 |
||||||||||||||||
157

8.102. Звести рiвняння задачi 8.98 до канонiчного виду, використовуючи результат задачi 8.101.
9Поверхнi другого порядку
Вцьому роздiлi використовуються такi поняття та результати.
1.Сфера. Рiвняння сфери. Координати центра, радiус сфери.
2.Цилiндричнi поверхнi. Рiвняння цилiндричної поверхнi. Напрямна, твiрна цилiндричної поверхнi. Цилiндричнi поверхнi другого порядку. Конiчнi поверхнi. Рiвняння конiчної поверхнi. Напрямна, вершина конiчної поверхнi. Конiчнi поверхнi другого порядку.
3.Поверхня обертання. Рiвняння поверхнi обертання. Твiрна обертання, вiсь обертання. Приклади поверхонь обертання другого порядку: елiпсоїд обертання, однопорожнинний i двопорожнинний гiперболоїди обертання, елiптичний параболоїд обертання.
4.Елiпсоїд, однопорожнинний гiперболоїд, двопорожнинний гiперболоїд, елiптичний параболоїд, гiперболiчний параболоїд: канонiчнi рiвняння. Прямолiнiйнi твiрнi однопорожнинного гiперболоїда, гiперболiчного параболоїда.
Приклади розв’язання задач
Приклад 9.1. Скласти рiвняння поверхнi, яка утворена обертанням навколо осi Oz кривої γ, яка лежить в площинi xOz, i задана рiвнянням:
а) F (x, z) = 0; |
в) |
x2 |
− |
z2 |
= 1; |
г) |
x2 |
− |
z2 |
= −1; |
||||
|
x2 |
|
z2 |
|
a2 |
c2 |
a2 |
c2 |
||||||
б) |
+ |
= 1; |
|
|
|
|
|
д) x2 = 2pz, p > 0. |
||||||
2 |
2 |
|
|
|
|
|
||||||||
|
a |
|
c |
|
|
|
|
|
|
|
|
|
|
|
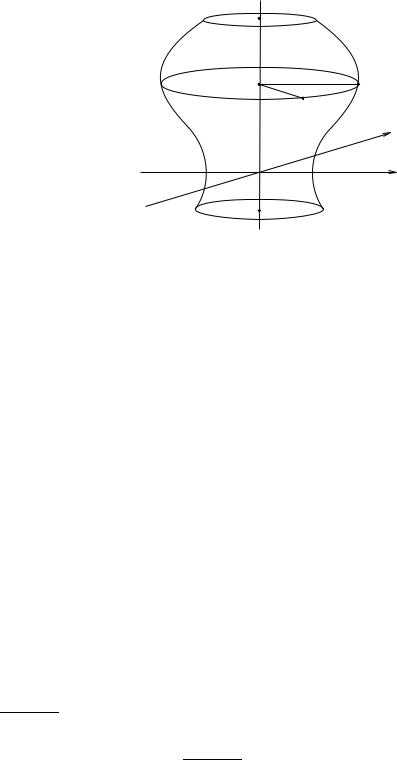
Розв’язання. a) Точка M (x, y, z) належить шуканiй поверхнi обертання тодi i тiльки тодi, коли знайдеться точка M0 (x0, 0, z0) заданої кривої
γтака, що точки M i M0 лежать на колi (позначимо його γ1), причому
•центр γ1 лежить на осi Oz,
158
 z
z
|
γ |
|
r |
|
0 |
r |
M0 |
γ |
M |
1 |
|
|
y |
O |
x |
•γ1 лежить в площинi, паралельнiй xOy (з цiєї умови випливає, що z = z0).
Оскiльки точка M0 належить γ, то F (x0, z0) = 0. |
|
|
|
|
Знайдемо вiдстань r вiд точки M до осi Oz : r = |
|
x2 + y2. Ця |
||
|
вiдстань r |
|
вiд |
|
вiдстань дорiвнює радiусу кола γ1. Аналогiчно, знайдемо |
p |
0 |
|
|
точки M0 до осi Oz : r0 = |x0|. Ця вiдстань так само дорiвнює радiусу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кола γ1, тобто r0 = r або x0 = ± |
|
x2 + y2. |
|
|
|
|||||||||||
Об’єднаємо всi знайденi |
умови в одну систему рiвнянь i вилучимо з |
|||||||||||||||
|
|
|
|
p |
|
|
|
|
|
|||||||
неї параметри x0, z0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z = z0, |
|
|
|
|
|
|
|
|
|
F ( |
|
|
x2 + y2, z) = 0. |
|||
|
F (x0, z0) = 0, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
± |
|
|
|
||
|
|
x |
2 |
|
|
y |
2 |
|
|
|
|
|
||||
x |
0 = ±p |
|
+ |
|
|
|
|
|
|
p |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отримане рiвняння i є рiвнянням шуканої поверхнi обертання.
Таким чином, якщо в площинi xOz крива γ задана рiвнянням F (x, z) = 0, то для того, щоб отримати рiвняння поверхнi обертання γ
навколо осi Oz, достатньо в цьому рiвняннi замiнити змiнну x на вираз p
±x2 + y2.
б) Скористаємось результатом пункту а) i замiнимо в рiвняннi кривої p
γ змiнну x на вираз ± x2 + y2. В результатi ми отримаємо рiвняння
159

поверхнi обертання елiпса |
x2 |
+ |
z2 |
= 1 навколо осi Oz : |
||||||
2 |
2 |
|
||||||||
|
a |
|
|
c |
|
|
|
|||
|
|
x2 |
|
y2 |
|
z2 |
||||
|
|
|
+ |
|
|
+ |
|
= 1. |
||
|
2 |
2 |
2 |
|||||||
|
|
a |
|
|
|
a |
|
c |
||
Отримана поверхня називається елiпсоїдом обертання.
|
z |
|
|
|
c |
γ |
y |
|
|
|
|
|
|
|
a |
-a |
O |
|
a x |
|
-a |
|
|
|
-c |
|
|
в) Скористаємось результатом пункту а) i замiнимо в рiвняннi кривої
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ змiнну x на вираз ±px |
2 |
|
|
y2. В результатi ми отримаємо рiвняння |
|||||||||
|
|
+x2 |
|
|
|
z2 |
|
|
|
||||
поверхнi обертання гiперболи |
|
|
− |
|
|
= 1 навколо осi Oz : |
|||||||
a2 |
|
c2 |
|||||||||||
|
|
|
x2 |
|
|
y2 |
|
z2 |
|||||
|
|
|
|
+ |
|
− |
|
= 1. |
|||||
|
|
|
a2 |
a2 |
c2 |
||||||||
Отримана поверхня називається однопорожнинним гiперболоїдом обертання.
г) Скористаємось результатом пункту а) i замiнимо в рiвняннi кривої
γ змiнну x на вираз ±p |
x2 |
|
|
y2. В результатi ми отримаємо рiвняння |
||||||||
|
|
+x2 |
z2 |
|||||||||
поверхнi обертання гiперболи |
|
|
− |
|
|
= −1 навколо осi Oz : |
||||||
a2 |
c2 |
|||||||||||
|
|
x2 |
|
y2 |
|
z2 |
||||||
|
|
|
+ |
|
− |
|
= −1. |
|||||
|
|
a2 |
a2 |
c2 |
||||||||
Отримана поверхня називається двопорожнинним гiперболоїдом обертання.
д) Скористаємось результатом пункту а) i замiнимо в рiвняннi кривої p
γ змiнну x на вираз ± x2 + y2. В результатi ми отримаємо рiвняння
160
