
2_Kinematyka
.pdf
Розділ 2
ОПИС МЕХАНІЧНОГО РУХУ (КІНЕМАТИКА)
2.1. Кінематика точки
Кінематика (від грецького κίνήματος (kinématos) - рух, зміна) - розділ механіки, в якому розглядаються способи математичного опису механічного руху тіл не торкаючись його причин.
Відповідний рівень абстракції в кінематиці такий, що матеріальний характер точок, які рухаються,
не має ніякого значення. Замість матеріальної точки в кінематиці можна оперувати поняттям точки відомим з геометрії і кінематика, таким чином, зводиться до вивчення геометричних властивостей руху тіл.
Залежно від характеристик об’єкту, рух якого вивчається, можна говорити про кінематику точки (відповідає моделі матеріальної точки), кінематику абсолютно твердого тіла та кінематику неперервно деформованих тіл, рідин та газів.
Основна задача кінематики точки та абсолютно твердого тіла1, які будуть розглянуті в цьому та наступному параграфах, є кількісний опис (за допомогою аналітичних виразів, графіків,
таблиць тощо) рухів, що їх здійснюють точки або тверді тіла відносно обраної системи відліку, і
визначення всіх кінематичних характеристик цих рухів. Кінематика розглядає також рухи віднос-
но систем відліку, що рухаються одна відносно одної, і зв’язок між кінематичними характеристиками руху відносно цих систем відліку.
Нижче ми розглянемо три способи опису руху точки: векторний, координатний та так званий природний.
2.1.1. Векторний спосіб
Нехай нас цікавить рух деякої точки A відносно деякої наперед заданої системи відліку.
Оберемо деяку точку O нерухому відносно цієї системи відліку. Назвемо її початком відліку.
Проведемо відрізок прямої з початку O до точки A . Напрямлений відрізок OA , тобто такий, для
1Надалі ми будемо вживати терміни тверде тіло та тіло , маючи на увазі тіла, що не деформується в процесі руху, замість більш довгого виразу абсолютно тверде тіло, якщо спеціально не вказано на деформованість цих тіл.

|
|
|
|
|
|
26 |
якого вказано початок (точка O ) |
та кінець (точка |
|
A |
|||
A )2, називають радіус-вектором r точки |
||||||
відносно початку O . При зміні з часом положення точки A вона описує в просторі криву, |
яка |
|||||
називається траєкторією точки A |
|
|
|
|||
(Рис. 2.1). При цьому змінюється і радіус-вектор r , тобто він є |
||||||
функцією часу t . Таким чином траєкторію точки |
A можна розглядати як геометричне місце |
|||||
|
|
3 |
. Рівняння траєкторії у векторному вигляді записують як залежність |
|||
кінців радіус-вектора r (t) |
|
|||||
радіус-вектора від часу |
|
|
|
|
|
|
|
|
|
|
(2.1) |
|
|
r |
r (t) |
|
|
|
|
|
Залежно від форми траєкторії розрізняють прямолінійний рух частинки, рух по колу,
криволінійний рух тощо.
Зауважимо, що поняття траєкторії застосовне
Рис. 2.1.
лише для макроскопічних тіл. Для мікрочастинок
(наприклад, електронів, протонів, нейтронів) поняття траєкторії у багатьох випадках або незастосовне зовсім або застосовне з обмеженою точністю.
2.1.2. Координатний спосіб |
|
|
|
Векторний спосіб є по суті геометричним і |
|
||
вельми наочним, але часто прагнуть до |
|
||
арифметизації опису руху. Для цього з обраною |
|
||
системою відліку зв’язують систему |
координат |
|
|
(декартову прямокутну, сферичну, циліндричну |
|
||
тощо). Вибір тієї чи іншої системи координат та її |
|
||
орієнтація визначається постановкою задачі, її |
|
||
симетрією та прагненням спростити розгляд руху. Як |
|
||
приклад розглянемо декартову прямокутну систему |
|
||
координат (Рис. 2.2). Положення |
точки |
A |
|
однозначно визначається трьома її координатами |
Рис. 2.2 |
||
x, y, z , які є функціями часу t : |
|
|
|
2 Це означає, що положення точок O і A визначено відносно системи відліку, наприклад, відстанями li від цих точок до тіл відліку системи відліку.
3 Поняттю траєкторії в аналітичній геометрії відповідає поняття годографа.
|
27 |
x x(t) , y y(t) , z z(t) |
(2.2) |
Ці три рівняння описують траєкторію точки |
A . У математиці такий спосіб задання кривої |
називається параметричним. Рівняння траєкторії в явному вигляді, тобто у вигляді рівняння, яке пов’язує між собою декартові координати x, y, z можна отримати виключаючи параметр t із
системи рівнянь (2.2).
На практиці часто початок системи координат зв’язують з одним із тіл відліку, а орієнтацію її осей задають за допомогою інших тіл відліку. Наприклад, у космонавтиці часто використовують систему координат, початок якої співпадає з центром мас космічного апарату, а осі напрямлені на обрані ―нерухомі‖, тобто дуже віддалені, зірки.
Зауважимо, що в останньому прикладі до системи відліку належить не тільки одне тіло відліку – космічний апарат, як часто вважають, а й тіла відліку – зірки, що забезпечують визначеність орієнтації осей.
Необхідно підкреслити, що яку б систему координат ми не обрали: декартову прямокутну, сферичну,
циліндричну або ще якусь, положення точки буде завжди визначатись трьома дійсними числами, що відбиває тривимірність простору, в якому ми живемо.
Між векторним та координатним способами опису руху точки існує найтісніший зв’язок,
зумовлений тим, що з точки зору математики задати координатну систему в просторі розмірності n означає задати n лінійно незалежних векторів (так званий векторний базис). На Рис. 2.2 такий
базис декартової прямокутної (ортогональної) системи координат утворено взаємно
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перпендикулярними одиничними векторами (ортами) i , j, k . Радіус-вектор r |
точки |
A відносно |
|||||||||||
початку O |
|
|
|
|
|
|
|
|
|
|
|
|
|
може бути поданий у вигляді суми трьох векторів-складових rx , |
ry , |
rz , напрямлених |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вдовж векторів i , j, k , тобто вздовж осей Ox,Oy,Oz : |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
rx |
ry |
rz . |
|
|
|
|
|
|
|
(2.3) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кожну з цих складових можна виміряти відповідним ортом: rx |
xi |
, |
ry |
yj |
, rz |
zk і |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подати радіус-вектор r в остаточному вигляді |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
xi |
|
yj |
zk , |
|
|
|
|
|
|
|
(2.4) |
|
де дійсні числа x, y, z у цій сумі за означенням є декартові координати точки A .

28
Підкреслимо, що радіус-вектор r є геометричний об’єкт, що існує незалежно від того, чи обрано
якусь систему координат чи ні. Тим більше радіус-вектор r не залежить від того, яку саме систему
координат обрано. В той же час координати x, y, z вектора |
|
|
|
|
r залежать від вибору системи координат. |
||||
|
|
|
|
|
Нехай точка A нерухома відносно обраної системи відліку. Тоді її радіус-вектор r є сталим, тобто його |
||||
|
r |
|
|
|
орієнтація відносно системи відліку і його довжина (модуль) |
r |
не змінюються з часом. Якщо тепер |
||
|
|
|
|
|
обирати різні декартові системи координат, то для одного й того ж самого вектора r |
отримаємо різні |
|||
набори координат. Наприклад, будемо по черзі обирати системи координат, в яких одна з координатних
|
|
|
Ox |
маємо x r, y 0, z 0 |
|
|
Oy |
осей направлена вздовж радіуса-вектора r . Тоді, |
при r |
|
; при r |
|
маємо x y, y r, z 0 ; при r Oz маємо x 0, y 0, z r .
Таким чином, систему відліку та систему координат не можна ототожнювати, як це іноді роблять.
Система відліку – це поняття суто фізичне, яке ґрунтується на виборі певних матеріальних об’єктів. Поняття системи координат – абстрактно-математичне. В одній і тій же фізичній системі відліку можна ввести безліч систем координат різних типів по-різному з нею пов’язаних, у тому числі й таких, що рухаються відносно цієї системи відліку. З огляду на це немає жодних підстав для включення системи координат до означення системи відліку як це іноді трапляється.
2.1.3. Природний спосіб
Якщо траєкторія руху точки наперед відома, то рух точки можна описати в такий спосіб. У
деякій точці траєкторії обирають початок відліку O , а також виділений напрям уздовж траєкторії.
(Рис. 2.3). Тоді положення точки A відносно початку O можна однозначно описувати дуговою координатою s – відстанню вздовж траєкторії від точки A
до початку O , взятою зі знаком плюс або мінус, залежно від того, в якому напрямку, у виділеному (додатному) чи у протилежному (від’ємному), треба рухатись вздовж
траєкторії з точки O , щоб досягти точки A .
Саме в такий природний спосіб найчастіше характеризують положення об’єкту або місце події в повсякденному житті, прив’язуючись до мережі транспортних
магістралей на поверхні Землі. Коли ми читаємо в газеті повідомлення про пригоду на такому-то кілометрі

29
залізниці Київ - Фастів, то ми дістаємо однозначне уявлення про місце події, незважаючи на те, що нам не
сповіщають ні його координати, ні його радіус-вектор.
2.1.4. Шлях, вектори переміщення, швидкості та прискорення
Введемо деякі поняття необхідні для більш повного опису руху матеріальної точки
(частинки). Нехай деяка частинка перемістилась з однієї точки простору в іншу.
Вектором переміщення або просто переміщенням частинки називають вектор, початок якого співпадає з початковим положенням частинки, а кінець — з її кінцевим положенням. Наприклад,
на Рис. 2.4 показано вектор переміщення із точки 1 в точку 2 позначений як r12 .
Рух частинки можна також характеризувати шляхом, що його проходить частинка при переміщенні з однієї точки простору в іншу. Шляхом називається довжина дуги траєкторії,
що з’єднує початкове та кінцеве положення частинки. На
Рис.2. 4 шлях на відрізку траєкторії частинки між точками 1 і 2
позначено як s12 .
Одному й тому ж вектору переміщення можуть відповідати різні траєкторії, і, відповідно, різні шляхи.
Переміщення за означенням є величина векторна, а шлях - скалярна, причому завжди додатно визначена, і їх не слід плутати. Нехай, наприклад, частинка рухається таким чином, що її кінцеве положення співпадає з початковим. При цьому переміщення дорівнює нулю (вектор переміщення є нуль-вектор), а шлях,
пройдений частинкою, не дорівнює нулю, а дорівнює довжині замкненої траєкторії.
|
|
|
|
|
|
|
|
|
|
|
|
|
Нехай радіус-вектор частинки в деякий момент часу t1 |
є |
r1 |
r (t1 ) , а в момент часу t2 — |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
r (t2 ) . З Рис. 2.4 видно, що вектор переміщення |
|
r12 r2 r1 |
можна розглядати як приріст r |
|||||||
|
|
|
|
t t2 t1 |
|
|
|
|
|
|
|
радіус-вектора r |
за проміжок часу |
: |
r |
r12 . |
Середнім вектором швидкості |
||||||
називають векторну величину |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
(2.5) |
|
|
|
t |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ясно, що |
|
r . Зрозуміло також, що середній вектор швидкості залежить від проміжку |
часу t , на якому він обчислюється. Якщо ми будемо при незмінному t1 , наприклад, зменшувати
t , то середній вектор швидкості буде змінюватись, в загальному випадку і за модулем і за

|
|
30 |
|
|
|
напрямком, оскільки буде змінюватись і приріст r |
радіус-вектора r |
набутий за цей проміжок |
часу. Точка 2, що визначає кінець вектора (Рис. 2.4), буде наближатися до точки 1. Можна r
|
|
поставити питання про границю, до якої прямує середній вектор швидкості |
при прямуванні |
t до нуля, а отже і при нескінченному наближенні точки 2 до точки 1. Ця границя буде характеризувати рух частинки в момент часу t1 , коли вона знаходиться в точці траєкторії 1, і
називається вектором швидкості або миттєвою швидкістю або просто швидкістю. Таким чином,
вектор швидкості в момент часу t визначається як границя
|
|
|
|
|
|
|
|
|
|
r (t t) r (t) |
|
r |
|
dr |
|||
lim |
t 0 |
|
|
lim |
t 0 t |
|
|
r . |
|
t |
dt |
||||||
|
|
|
|
|
||||
В математиці така границя називається похідною радіус-вектора
(2.6)
|
|
r |
за часом t 4. Вектор |
|
|
швидкості |
направлений так само як нескінченно малий вектор елементарного переміщення dr , |
що здійснюється за нескінченно малий проміжок часу dt , тобто по дотичній до траєкторії в точці,
де знаходиться частинка в момент часу t . Отже вектор швидкості частинки направлений по дотичній до її траєкторії в напрямі руху. Модуль швидкості визначається як модуль вектора
швидкості :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
dr |
|
|
dr |
|
ds |
|
ds |
|
r |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim s 0 |
|
|
|
|
|
, |
|
(2.7) |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
dt |
|
ds |
dt |
dt |
|
|
s |
|
|
|
||||||||||||||
|
|
|
||||||||||||||||||||||||
Оскільки при t 0 |
різниця між довжиною хорди |
та довжиною дуги s , яку вона |
||||||||||||||||||||||||
r |
||||||||||||||||||||||||||
стягує, прямує до нуля, тобто |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
lim |
s 0 |
r 1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.8) |
|||||||||
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
то для модуля швидкості справедлива рівність |
|
|
||||||||||||||||||||||||
|
ds |
|
s . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.9) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
Похідну за часом (і лише її!) в механіці часто позначають крапкою над відповідною функцією часу, як це |
|
|
|
зроблено в правій частині виразу (2.6). |
31
Таким чином, модуль швидкості дорівнює похідній шляху за часом, яка в свою чергу може
бути подана як відношення елементарного шляху ds до нескінченно малого проміжку часу який частинка проходить цей шлях.
Із уведених означень випливає зв’язок між швидкістю та елементарним переміщенням
dr dt
і між модулем швидкості та елементарним шляхом
ds dt .
dt , за
(2.10)
(2.11)
Ці співвідношення можуть бути використані для обчислення переміщення і шляху частинки за скінченні проміжки часу шляхом інтегрування (послідовного додавання) елементарних переміщень чи шляхів.
Наприклад, якщо відома залежність модуля швидкості від часу, то шлях, який проходить частинка за проміжок часу t2 t1 , можна обчислити за формулою, що безпосередньо випливає з
(2.11)
t2 |
|
s12 (t)dt |
(2.12) |
t1 |
|
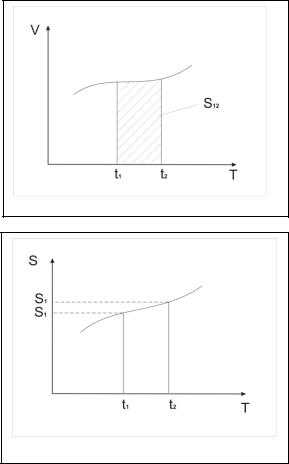
Геометричну інтерпретацію цього інтегрування подано на
Рис. 2.5: шуканий шлях s12 на графіку залежності модуля швидкості від часу t чисельно дорівнює
заштрихованій площі під кривою. Елементарний шлях
зобразився б на такому графіку нескінченно вузьким
(шириною dt ) вертикальним прямокутником висотою
. На Рис. 2.6 показано графік залежності пройденого
частинкою шляху s від часу t . Модуль швидкості
частинки в будь-який момент часу може бути визначений з такого графіка як кутовий коефіцієнт дотичної до кривої.
Для відшукання переміщення частинки за деякий
проміжок часу t2 t1 треба діяти аналогічно,
використовуючи (2.10):
|
t2 |
|
r12 |
(t)dt |
|
|
t1 |
|
Рис. 2.5
Рис. 2.6
(2.13)
32
Це дає можливість записати формули для відшукання швидкості в такому вигляді
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
s12 |
|
|
|
(t)dt |
|
|
||
|
|
|
|
|
|
|
t1 |
|
|
(2.14) |
||
|
t |
2 |
t |
1 |
t |
2 |
t |
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
(t)dt |
|
|
||||
|
r |
|
|
|
t |
|
|
|
|
|||
|
|
|
12 |
|
|
|
1 |
|
|
|
(2.15) |
|
t |
2 |
t |
|
t |
2 |
t |
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
||
Як уже відзначалося, швидкість частинки в загальному випадку змінюється з часом. Ці зміни |
||||||||||||
|
(t) |
|
можна охарактеризувати відношенням нескінченно малого (елементарного) |
|||||||||
величини |
|
|||||||||||
приросту вектора швидкості до нескінченно малого проміжку часу, за який цей приріст набуто,
|
|
|
|
|
тобто похідною від (t) за часом: |
|
|||
|
|
|
|
|
|
d |
(2.16) |
||
a lim t 0 |
t |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
Величина a |
називається вектором прискорення або просто прискоренням частинки. Вектор |
|||
прискорення співпадає |
з напрямом елементарного приросту вектора швидкості |
|
||
d , а не з |
||||
напрямом самого вектора швидкості .
Підставляючи в (2.16) вираз для швидкості з (2.6) отримаємо
|
|
|
d (t) |
||
a(t) |
|
|
dt |
||
|
|
d |
|
|
|
|
|
|
|
dr (t) |
|
d 2r (t) |
||||
|
|
|
|
|
|
||
|
|
|
2 |
||||
|
dt |
dt |
|
|
dt |
||
|
|
|
(2.17) |
r (t) , |
звідки випливає, що прискорення частинки є другою похідною за часом від її радіус-вектора.
Отже, якщо відомий закон руху частинки, поданий як залежність її радіус-вектора від часу,
, то шляхом послідовного диференціювання радіус-вектора за часом можна знайти r r (t)
швидкість і прискорення частинки в будь-який момент часу.
Наведені вище співвідношення між прискоренням, швидкістю і радіус-вектором частинки можуть бути записані і в координатній формі. Наприклад, проектуванням відповідних векторних рівностей на осі декартової системи координат отримаємо для компонент радіус-вектора, швидкості та прискорення такі вирази
x x(t) , |
|
|
(t) |
dx |
x |
(t) , |
a |
(t) |
d |
x |
|
d 2 x |
x(t) |
|
x |
|
|
|
|
2 |
|||||||||
|
|
|
dt |
|
|
x |
|
dt |
|
|
dt |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||

33
y y(t) , |
|
|
(t) |
dy |
y |
(t) , |
a |
|
(t) |
d y |
|
|
d 2 y |
y(t) |
(2.18) |
||||||||
y |
dt |
y |
dt |
|
dt |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z z(t) , |
|
|
(t) |
|
dz |
|
z(t) , |
a |
|
(t) |
|
d |
z |
|
|
d 2 z |
|
z(t) |
|
||||
z |
|
dt |
z |
|
dt |
|
|
|
dt |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким чином, якщо задано закон руху частинки в координатній формі, як залежність її координат від часу, можна знайти проекції векторів швидкості і прискорення на координатні осі, а отже й самі вектори.
Наприклад, модуль вектора :
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
(x)2 ( y)2 (z)2 . |
|
||
|
(2.19) |
||||||||
|
|
|
x |
y |
z |
|
|
|
|
При цьому напрям вектора швидкості визначається кутами, які він утворює з осями Ox,Oy,Oz
(Рис. 2.7) і які можна знайти за напрямними косинусами:
cos x , cos y , cos z . (2.20)
На практиці часто виникає обернена задача: за відомою залежністю прискорення частинки від часу
|
|
|
a(t) знайти залежність від часу її швидкості |
(t) та |
|
положення (радіуса-вектора |
|
разом |
r (t) ), які |
||
визначають так званий механічний стан частинки. Ця задача може бути розв’язана однозначно лише тоді, Рис. 2.7.
коли відомі так звані початкові умови, а саме швидкість та радіус-вектор частинки в деякий
початковий момент часу t 0 , відповідно (0) та r (0) , тобто її початковий механічний стан.
Дійсно, за відомим прискоренням a(t) ми можемо, користуючись означенням прискорення (2.16),
отримати лише приріст швидкості за проміжок часу (0,t) :
t
(t) a(t)dt
0 |
(2.20) |
|
Щоб знайти саму швидкість у момент часу t треба до цього приросту додати початкову швидкість
|
|
|
|
t |
|
(t) (0) |
|
(t) (0) |
a(t)dt. |
0 |
(2.21) |
|

Аналогічно розв’язується питання і про радіус-вектор:
|
|
|
|
t |
|
r (t) r (0) |
r (t) r (0) |
(t)dt. |
|||
|
|
|
|
0 |
|
|
|
|
|
|
|
де для знаходження r використано формулу (2.13), а (t) повинно бути взяте з (2.21).
34
(2.22)
Така обернена задача є практично важливою і розв’язується, наприклад, у так званих інерціальних системах навігації різноманітних рухомих об’єктів, таких як літаки, підводні човни, балістичні та крилаті ракети. В таких системах шляхом двократного інтегрування безперервно вимірюваних на борту компонент вектора прискорення за відомими координатами старту (початкова умова) визначають поточні координати рухомого об’єкта без спостереження яких би то не було зовнішніх орієнтирів.
2.1.5. Прискорення частинки, що рухається по криволінійній траєкторії
Вектор швидкості частинки може бути поданий у вигляді добутку модуля швидкості на
|
|
|
|
|
|
|
|
|
|
|
|
||
одиничний вектор |
|
направлений вздовж : |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.23) |
. |
|
|
|
|||
Підставляючи (2.20) в (2.12), дістанемо |
|
|||||
|
|
d ( ) |
|
|
|
(2.24) |
a(t) |
|
|
, |
|||
|
|
|
|
|
|
|
dt
тобто вектор прискорення частинки в загальному випадку можна подати у вигляді двох
складових, одна з яких, , направлена так само як швидкість, тобто по дотичній до траєкторії, а
друга, , як ми покажемо нижче, перпендикулярна до першої.
Друга складова існує лише тоді, коли частинка рухається по криволінійній траєкторії. Ми дослідимо її більш детально, обмежившись випадком плоскої траєкторії, тобто такої, яка повністю лежить в одній площині. У випадку довільної гладенької плоскої кривої в будь-якій її точці (наприклад, у точці 1 на Рис. 2.8) можна побудувати так зване стичне коло (круг кривини),
яке найщільніше прилягає до кривої в точці 1 порівняно з будь-якими іншими колами, що дотикаються до кривої в тій самій точці 1. Центр стичного кола називають центром кривини, а
радіус - радіусом кривини R кривої в даній точці.5 Апроксимація (наближення) ділянки траєкторії
5Іноді користуються оберненою до радіусу кривини величиною R 1 , яка зветься просто кривиною кривої в даній точці.
