Praktika_III_Algoritmy

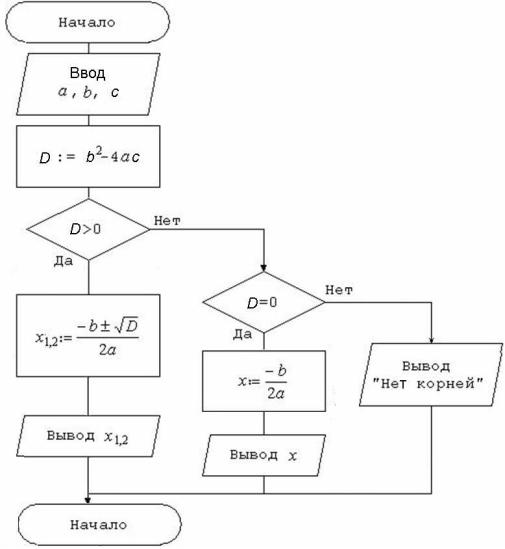
Рис. 3.6. Блок-схема решения квадратного уравнения

Задачи и упражнения

Записать алгоритмы решения следующих задач с помощью блок-схем.

1.Даны две точки A(x1,y1) и В(x2,y2). Определить, которая из точек находится ближе к началу координат.

3.Даны три положительных числа. Определить, можно ли построить треугольник с длинами сторон, равным этим числам. Если можно, то ответить на вопрос, является ли он остроугольным.

11

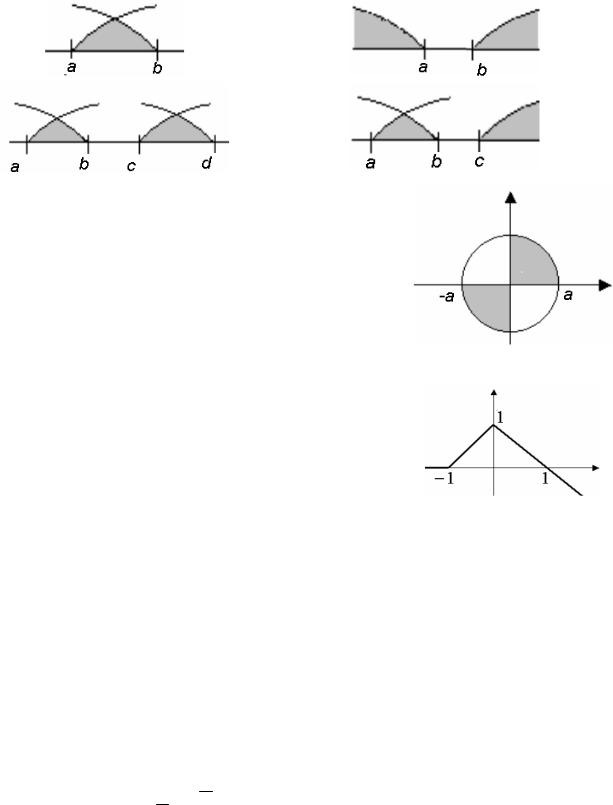
4. Определить принадлежит ли значение x одному из отрезков

5.Определить принадлежит ли некоторая точка М с произвольными координатами х, y заштрихованной области.

6.Вычислить значение функции, заданной графически.

7.Определить в какой четверти находится точка с координатами x,y.

9.Заданы три положительных числа a, b и с. Определить являются ли они последовательно стоящими элементами арифметической прогрессии. Если являются, то определить разность прогрессии.

10.Дано число x. Вывести в порядке возрастания значения функций:

sin x, tg x, ln x, 1 , x Если при каком либо x некоторые из выра- x

жений не имеют смысла, вывести сообщение об этом и сравнивать значения только тех, которые имеют смысл.

12

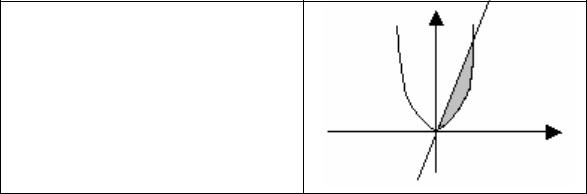
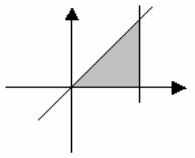
11.Определить принадлежит ли точка с координатами x,y заштрихованной области

,

.

Циклические алгоритмические структуры. Циклические структуры обеспечивают многократное выполнение одной и той же последовательности действий для различных значений, входящих в них переменных. Изменяющиеся в цикле переменные называются пе- ременными цикла. Алгоритм циклической структуры должен содержать:

1.подготовку цикла – задание начальных значений переменных цикла перед первым его выполнением;

2.тело цикла – действия, которые выполняются при различных значениях переменных цикла;

3.изменение значений переменных цикла перед его новым повторением;

4.управление циклом – проверку условия окончания цикла или перехода на начало тела цикла.

Существует два типа элементарных циклических структур:

-цикл с параметром или с повторением,

-цикл с условием.

Циклы с параметром

Циклы с параметром используют тогда, когда количество повторов тела цикла заранее известно. Цикл повторяется пока значение параметра цикла k лежит в интервале [a,b], причем, если a и b являются выражениями, они вычисляются только один раз в начале цикла. Параметр цикла, начальное и конечное значения должны быть одинакового типа. Схематично такой цикл изображен на рис. 3.7.

13

Выполняется такая структура следующим образом:

1.Параметру цикла k присваивается начальное значение a и сравнивается с конечным значением b. Если начальное значение параметра цикла превышает (при положительном шаге цикла) конечное значение, то тело цикла ни разу не выполнится.

2.Выполняется тело цикла.

3.Текущее значение параметра цикла k увеличивается (или уменьшается) на значение шага h. Результат операции k+h присваивается параметру цикла k, старое значение при этом теряется.

4.Проверяется условие окончания цикла: текущее значение параметра сравнивается с конечным значением b. Если значение параметра цикла становится больше конечного (при положительном шаге h), то происходит выход из цикла, иначе происходит переход к пункту 2.

Рис. 3.7. Алгоритмическая структура «Цикл с параметром»: k– параметр цикла, a– начальное значение параметра цикла,

b– конечное значение параметра цикла, h– шаг изменения параметра цикла

Пример 3.4. Вычислить значения функции y = f(x) от некоторой переменной х, изменяющейся от начального значения х0 до конечного хk с постоянным шагом h (протабулировать функцию на заданном промежутке [х0 , хk] с шагом h). Записать алгоритм решения задачи с помощью блок-схемы.

Объекты алгоритма: a, b, h, x, y числового типа. Словесная запись алгоритма:

Поскольку известно начальное и конечное значение переменной х и шаг его изменения (известно, сколько раз выполняется цикл), то для реализации алгоритма используем циклическую структуру типа

14

«Цикл с параметром». Параметром цикла в этом случае является переменная x.

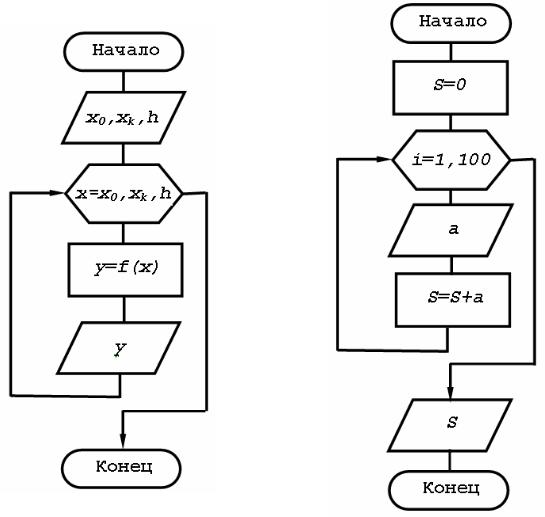
Блок-схема алгоритма: представлена на рис. 3.8.

Пример 3.5. Найти сумму 100 чисел. Записать алгоритм решения задачи с помощью блок-схемы.

Алгоритм решения: вычисление суммы организуется в виде циклического алгоритма, когда при каждом прохождении цикла номер слагаемого увеличивается на 1, а сумма изменяется на величину введенного i-го слагаемого. Цикл повторяется до тех пор, пока не будут просуммированы все 100 слагаемых. Для того чтобы начальное значение суммы не исказило результат, его обнуляют.

Блок-схема алгоритма представлена на рис. 3.9. 15

Циклы с условием

Циклы с условием используются в том случае, если количество повторений тела цикла заранее неизвестно, но задано условие его окончания, причем количество повторений может быть определено в ходе самих вычислений. Если условие окончания цикла проверяется перед выполнением тела цикла, то такие циклические структуры называют циклами с предусловием. Если проверка условия происходит после выполнения тела цикла – циклами с постусловием.

Алгоритмическая структура типа «Цикл с предусловием» изображена на рис. 3.10. Значение логического выражения в условии вычисляется перед каждым выполнением тела цикла. Если значение истинно, то тело цикла выполняется и снова вычисляется выражение условия. Если результат имеет ложное значение, происходит выход из цикла. Таким образом, цикл продолжает свою работу, пока значение логического выражения остается истинным.

Алгоритмическая структура типа «Цикл с постусловием» изображена на рис. 3.11. Вначале выполняется тело цикла, затем проверяется условие выхода из цикла. Если значение логического выражения ложно, тело цикла выполняется еще раз, если истинно – происходит выход из цикла. Таким образом, цикл продолжает свою работу, пока значение логического выражения остается ложным. Тело цикла с постусловием выполняется всегда хотя бы один раз.

Замечание 1. Чтобы циклы с условием успешно завершались, необходимо, что- бы в теле цикла был хотя бы один оператор, изменяющий значения, входящих в логическое выражение переменных.

16

Пример 3.6. Определить количество цифр в целом числе N в десятичной СС. Записать алгоритм решения задачи с помощью блоксхемы.

Алгоритм решения:

Количество цифр в числе вычисляется последовательным делением числа N на 10 до тех пор, пока целая часть числа не станет равной нулю. Количество произведенных делений будет равно числу цифр. Поскольку не известно сколько раз будет выполняться деление, то для реализации алгоритма используем циклическую структуру типа «Цикл с условием». Условие окончание цикла: равенство нулю целой части числа после деления.

Блок-схема алгоритма представлена на рис. 3.12. Здесь k– количество делений, [ ] – выделение целой части числа.

алгоритм решения задачи с помощью блок-схемы.

Алгоритм решения: Вычисление суммы организуется в виде циклического алгоритма. При каждом прохождении цикла номер слагаемого увеличивается на 1, а сумма увеличивается на величину i-го слагаемого. Поскольку для вычисления сумм бесконечного ряда количество слагаемых заранее неизвестно, то для реализации алгоритма используем циклическую структуру типа «Цикл с условием». Условие окончание цикла: модуль очередного слагаемого становится меньше заданной точности вычислений ε: ai < ε . Для того чтобы начальное значение суммы не исказило результат, его обнуляют перед циклом.

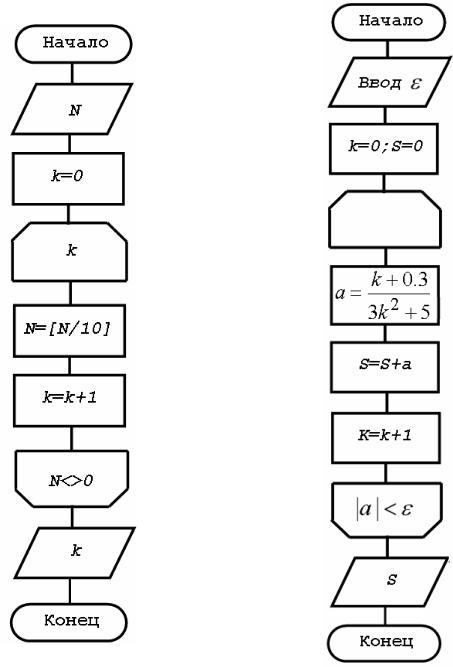
Блок-схема алгоритма представлена на рис. 3.13.

17

Использование рекуррентной формулы для вычисления суммы ряда

Рекуррентной называется всякая формула, выражающая каждый член последовательности через предыдущие члены этой последовательности.

В некоторых случаях при вычислении суммы ряда целесообразно последующий член суммы вычислять, используя предыдущий для

18

уменьшения общего количества арифметических операций и избавления от больших чисел. Как правило, в этом случае рекуррентная формула имеет вид: ak +1 = c × ak . Из этого равенства можно найти коэффициент С, на который умножается предыдущий член последовательности, для того чтобы найти следующий:

c = ak +1 . ak

Таким образом, если известно первое слагаемое и коэффициент С, то можно найти любой член последовательности.

Пример 3.8. Сравнить значение функции sin(x) и значение суммы бесконечного степенного ряда, который получается разложением этой функции в степенной ряд:

Подсчитать количество слагаемых, обеспечивающих заданную точность разложения.

Алгоритм решения: Число членов данного ряда заранее неизвестно и определяется по заданной точности вычисления искомой функции. Кроме того, по соображениям упрощения используемых математических выражений целесообразно организовать вычислительный процесс так, чтобы очередной член этого ряда вычислялся с использованием уже вычисленного предыдущего члена ряда, избавляясь при этом от необходимости возведения в степень и вычисления факториала для каждого слагаемого. Коэффициент С вычисляется по формуле:

Для реализации алгоритма используем циклическую структуру типа «Цикл с условием». Условие окончание цикла: модуль разности значения функции sin(x) и значения суммы становится меньше заданной точности вычислений ε: ai < ε .

Блок-схема алгоритма представлена на рис. 3.14.

19

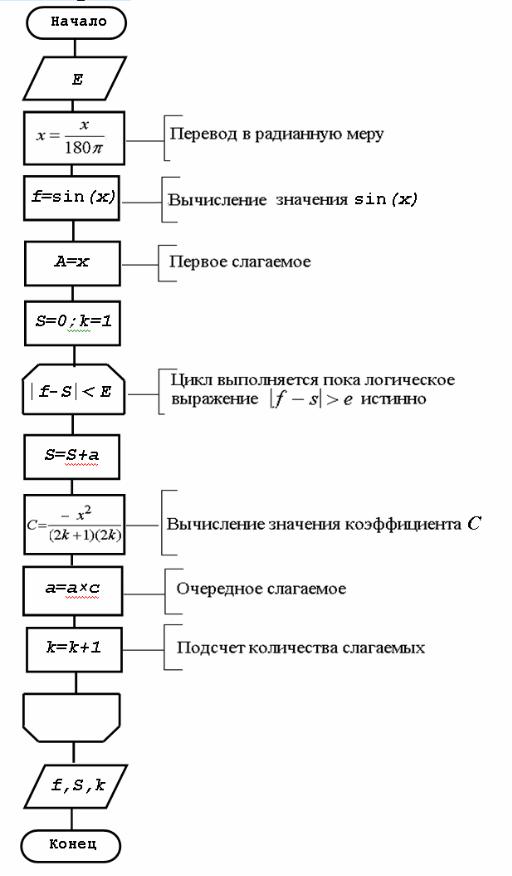
Рис. 3.14. Вычисление бесконечной суммы ряда с помощью рекуррентной формулы

20