
razdel1UMK
.pdf
для проекций векторов на ось справедливы следующие теоремы (без доказательств).
Теорема 1.8. Проекция суммы векторов на ось равна сумме проекции слагаемых векторов на ту же ось:
пр l ( |
|
1 + |
|
|
2 +K+ |
|
|
k )=прl |
|
1 + прl |
|
2 +K+ прl |
|
|
k . |
|
|||||||||||||||
a |
a |
a |
a |
a |
a |
(1.35) |
|||||||||||||||||||||||||
Теорема 1.9. Если вектор |
|
|
умножить на число λ, то его проекция на ось |
||||||||||||||||||||||||||||
a |
|||||||||||||||||||||||||||||||
умножится на это число: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
пр l (λ |
|
)=λ прl |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
a |
a |
|
|
|
|
|
|
|
|
(1.36) |
|||||||||||||||||||||
|
|
|
|
|
|
1.6.4 Линейная комбинация векторов. Базис |
|
||||||||||||||||||||||||
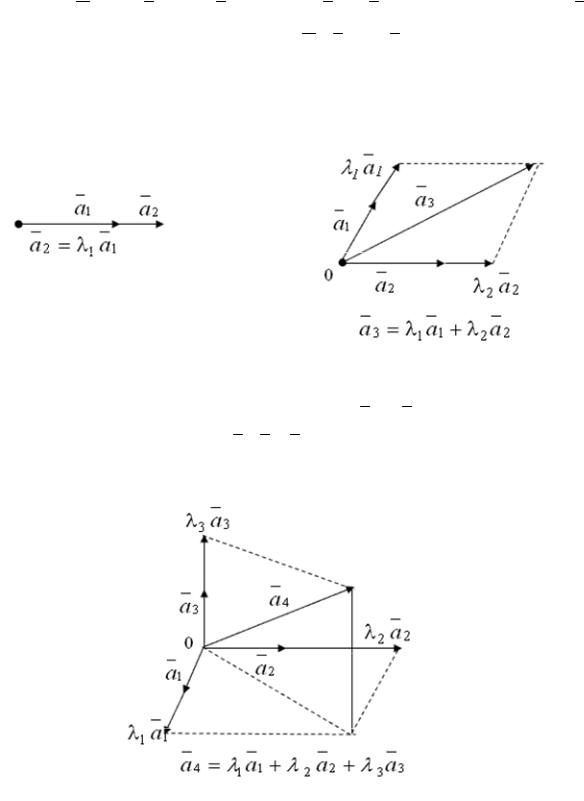
ОПРЕДЕЛЕНИЕ 1.31 Пусть заданы векторы |
|
1, |
|
2 ,K, |
|
k |
|
||||||||||||||||||||||||
a |
a |
a |
и числа |
||||||||||||||||||||||||||||
λ1, λ2 ,K, λk . Выражение λ1 |
|
1 + λ2 |
|
2 +K+ λk |
|
k |
называется линейной |
||||||||||||||||||||||||
a |
a |
a |
|||||||||||||||||||||||||||||
комбинацией векторов a1,a 2 ,K,a k . Очевидно, что линейная комбинация векторов является вектором. Рассмотрим особый случай, когда
λ1 |
|
1 + λ2 |
|
2 +K+ λk |
|
k = |
|
. |
|
a |
a |
a |
0 |
(1.37) |
|||||
ОПРЕДЕЛЕНИЕ 1.32 Если равенство (1.37) возможно только при всех |
|||||||||
λ1, λ2 ,K, λk , равных нулю, то векторы a1,a 2 ,K,a k называются линейнонезависимыми. Если же это равенство справедливо не при всех λ i = 0, где i =1,2,K, k , то векторы называются линейно-зависимыми.
Пусть a1,a 2 ,K,a k линейно-зависимы. Тогда среди λ i найдется хотя бы одно не равное нулю число. Пусть λ1≠ 0. Разделив обе части равенства (1.37) на λ1, получим
|
|
1 |
= − |
λ 2 |
|
2 |
− |
λ 3 |
|
3 |
−K− |
λ k |
|
|
|
k = μ 2 |
|
2 +μ 3 |
|
3 +K+μ k |
|
k , |
|||||
|
a |
a |
a |
a |
a |
a |
a |
||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
λ 1 |
|
λ 1 |
|
|
|
|
λ 1 |
|
|
|
|
|
|
|
|
|
|
|||||
где μ2 |
= − |
λ 2 , μ |
3= −λ 3 |
, K, μ k = − |
|
λ k |
. |
||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
λ |
1 |
|
|
|
λ |
1 |
|
|
|
|
|
|
λ |
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Выражение μ 2a 2 +μ 3a3 +K+μ k a k является линейной комбинацией
векторов a 2 ,a3 ,K,a k . Итак, если векторы линейно-зависимы, то хотя бы
один из них является линейной комбинацией остальных.
Справедливо и обратное утверждение: если хотя бы один вектор является линейной комбинацией других векторов, то вся группа векторов линейнозависима. Пусть, например, a 1 =μ 2a 2 +μ 3 a3 +K+μ k a k .
41
Тогда −a 1 +μ 2a 2 +μ 3 a3 +K+μ k a k = 0 и коэффициент при a1
отличен от нуля. Это означает, что вектора a 1,a 2 ,K,a k линейно-зависимы.
Примерами линейно-зависимых векторов являются любые два вектора прямой; любые три вектора плоскости; любые четыре вектора пространства
(рис. 1.12-1.13).
Рис. 1.12
Рис. 1.13
В то же время два неколлинеарных вектора a1 и a 2 плоскости (рис. 1.13)
или три некомпланарных вектора a1,a 2 ,a3 пространства (рис. 1.14) являются примерами линейно-независимых векторов.
Рис. 1.14
ОПРЕДЕЛЕНИЕ 1.33 Любая группа, составленная из максимального
числа линейно-независимых векторов некоторого пространства R n , называется базисом этого пространства. Число векторов базиса называется
размерностью пространства. Так, базисом на прямой (пространство R1 )
42

является любой ненулевой вектор этой прямой. Размерность прямой равна
единице. Базисом на плоскости (пространство R 2 ) являются любые два неколлинеарных вектора этой плоскости. Размерность плоскости равна двум.
Базисом в объемном пространстве (пространство R 3) являются любые три некомпланарные вектора. Размерность этого пространства равна трем.
Пусть векторы a1,a 2 ,K,a n образуют базис R n . Тогда любой вектор a этого пространства является линейной комбинацией базисных векторов, то есть
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= λ1 |
|
|
|
1 + λ2 |
|
2 +K+ λ n |
|
n . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
a |
a |
(1.38) |
|
|
|
|||||||||||||||||||||||
Представление вектора |
|
|
|
|
в форме (1.38) называется разложением этого |
||||||||||||||||||||||||||||||||||||||||||
a |
|||||||||||||||||||||||||||||||||||||||||||||||
вектора по базисным векторам. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Числа λ1,λ2 ,K,λn |
разложения называются координатами вектора |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
a |
|||||||||||||||||||||||||||||||||||||||||||||||
по базису |
|
1, |
|
2 ,K, |
|
|
|
n . Этот факт записывается в виде |
|
= {λ1 ;λ2 ;Kλn }. |
|
|
|
||||||||||||||||||||||||||||||||||
a |
a |
a |
a |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Векторы λ1 |
|
1,λ2 |
|
|
|
2 ,K,λn |
|
n называется компонентами вектора |
|
по |
|||||||||||||||||||||||||||||||||||||
a |
a |
a |
|||||||||||||||||||||||||||||||||||||||||||||
a |
|||||||||||||||||||||||||||||||||||||||||||||||
базисным векторам |
|
1, |
|
2 ,K |
|
n . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
a |
a |
a |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1, |
|
2 ,K |
|
n , образующие базис, имеют общее начало |
0 |
|||||||||||||||||||||||||||||||||
Если векторы |
|
|
a |
a |
a |
||||||||||||||||||||||||||||||||||||||||||
и вектор |
|
= |
|
, |
|
|
|
где |
M − некоторая точка пространства, |
то числа |
|||||||||||||||||||||||||||||||||||||
a |
OM |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
λ1,λ2 ,K,λn называются также координатами этой точки. Этот факт |
||||||||
записывают в виде M (λ1;λ2 ;K;λn |
). |
|
|
|
|
|
|
|
1.6.5 Прямоугольная декартова система координат |
|
|
|
|
|
|
|
|
ОПРЕДЕЛЕНИЕ 1.34 Пусть |
в пространстве R 3 векторы |
|
|
1, |
|
2 , |
|
3 |
a |
a |
a |
||||||
образуют базис этого пространства. |
Выберем в R 3 произвольную точку O и |
|||||||
отложим с началом в этой точке базисные векторы. Совокупность точки O и |
||||||||
трех базисных векторов называется системой координат в пространстве R 3. |
||||||||
Ввиду произвольности выбора точки и выбора базисных векторов в R 3 можно |
||||||||
построить бесконечное множество |
систем координат. Выберем |
в качестве |
||||||
базисных векторов три взаимно перпендикулярных единичных вектора
i = a10 , j = a 02 , k = a30 . Совокупность точки O и базисных векторов i, j,k
называется прямоугольной декартовой системой координат в пространстве
R 3.
Выберем в R 3 произвольную точку M и построим вектор OM. Так как векторы i, j,k образуют базис, то согласно (1.38) вектор OM можно разложить
на компоненты по этому базису: |
|
OM = λ1 i + λ2 j + λ3 k , |
(1.39) |
43
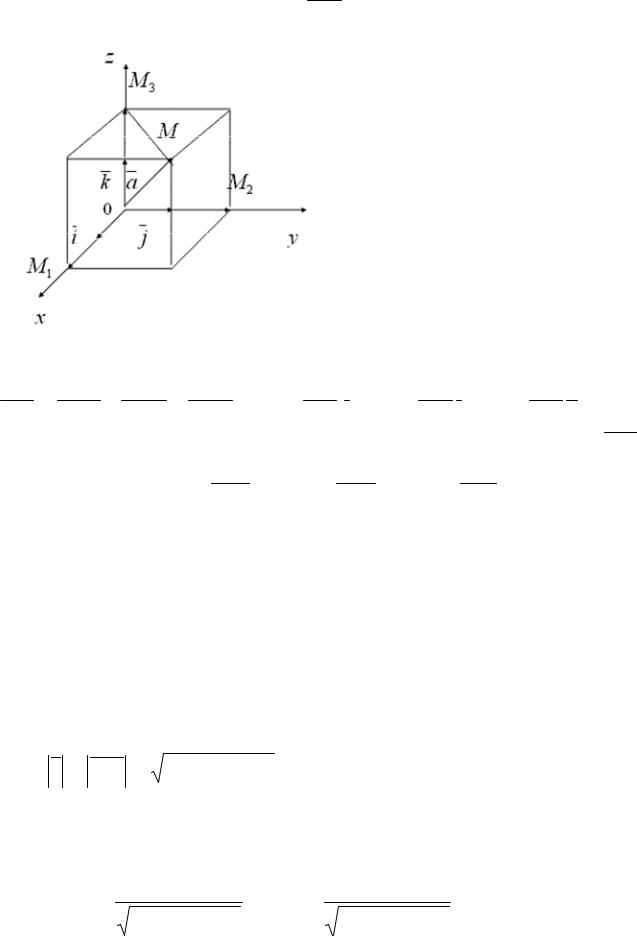
где λ1 ,λ2 ,λ3 − координаты вектора OM в заданном базисе.
Проведем через точку O в
направлении |
векторов |
|
|
|
|
|
|
|
|
оси |
i, j,k |
||||||||||
0X,0Y, 0Z |
соответственно |
и |
||||||||
спроектируем |
вектор |
|
|
|
|
на |
||||
|
|
OM |
||||||||
каждую из осей (рис. 1.15). |
|
|||||||||
Пусть |
точки M1, M2 , M3 |
|||||||||
есть проекции точки M на оси абсцисс, ординат и аппликат соответственно.
Рис. 1.15
Тогда
OM = OM1 + OM2 + OM3 =прOX OM i + прOY OM j + прOZ OM k . (1.40)
Из сравнения (1.40) с (1.39) следует, что координаты вектора OM определяется по формулам
λ1 =прox OM, λ2 =прoy OM, λ3 =прoz OM..
Впрямоугольной декартовой системе эти координаты принято
обозначать через x, y, z соответственно |
|
и называть |
прямоугольными |
|||||||||||||||||||
декартовыми координатами вектора |
|
|
|
|
или декартовыми координатами |
|||||||||||||||||
OM |
||||||||||||||||||||||
точки M R 3. Итак, |
|
|
|
|
||||||||||||||||||
|
|
|
|
= λ1 |
|
+λ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
OM |
i |
j +λ3 k = xi + y j + zk ={x; y;z}. |
(1.41) |
||||||||||||||||||
Координаты точки M R 3 записываются в форме |
M(x; y; z) Пусть |
|||||||||||||||||||||
вектор |
|
= |
|
задан в координатной форме |
|
|
= {x; y;z}. Так как этот вектор |
|||||||||||||||
a |
OM |
a |
||||||||||||||||||||
совпадает с диагональю прямоугольного параллелепипеда (рис.1.15), то его длина равна длине этой диагонали. Следовательно,
a = OM = x 2 + y2 + z2 |
(1.42) |
|
Обозначим через α,β, γ углы, между вектором |
|
и осями координат |
a |
||
OY, OY, OZ . Тогда из прямоугольных треугольников |
|
|
OMM1, OMM2 , OMM3 получим |
|
|
cos α = |
x |
, cosβ = |
y |
, |
x 2 + y2 + z2 |
x 2 + y2 + z2 |
44

cos γ = |
z |
(1.43) |
x 2 + y2 + z2 |
ОПРЕДЕЛЕНИЕ 1.35 Косинусы углов α,β,γ , определяемые по (1.43),
называются направляющими косинусами вектора a . Нетрудно проверить,
что направляющие косинусы связаны между собой соотношением
|
|
cos2 α + cos2 β+ cos2 γ =1 |
|
|
|
|
|
|
(1.44) |
||||||||||||||||||||||||||||||||||
|
|
ПРИМЕР 1.21 Доказать, что в прямоугольной декартовой системе |
|||||||||||||||||||||||||||||||||||||||||
координат векторы |
|
|
|
|
|
|
|
имеют координаты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
i, j,k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
={1;0;0}, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
i |
j ={0;1;0}, k ={0;0;1}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Доказательство. Так как векторы |
|
|
|
|
|
|
образуют базис прямоугольной |
||||||||||||||||||||||||||||||||||
|
|
i, j,k |
|||||||||||||||||||||||||||||||||||||||||
декартовой |
|
системы |
координат, |
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= |
|
|
|
=1. |
|||||||||||
|
|
|
|
|
i |
j,i k, j k, |
i |
j |
k |
||||||||||||||||||||||||||||||||||
Следовательно, прi i =1, прj i = 0, прk i = 0
Но прi i = прOX i, прj i = прOY i, прk i = прO Z i
По формуле (1.38) получим, что
i = (прOX i)i + (прOY i)j + (прOZ i)k =1i + 0j + 0k = {1;0;0}.
Аналогично доказываются оставшиеся равенства.
1.6.6 Линейные операции над векторами, заданными в координатной форме
Пусть векторы a1 и a 2 заданы в координатной форме:
a1 = {x1; y1;z1}= x1i + y1 j + z1 k, (1.45) a 2 = {x 2 ; y2 ;z2 }= x 2 i + y2 j + z2 k.
Непосредственно из теорем 1.5 и 1.6 о проекциях векторов на ось и определения координат вектора (1.38) вытекают правила:
|
|
|
|
|
= |
|
|
|
|
|
|
, если |
x1 = x 2 , y1 = y2 , z1 = z2 ; |
|
|
||||||||||||||||||||||||||
|
|
|
a1 |
a 2 |
(1.46) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
+ |
|
|
|
|
|
= (x1 |
+ x 2 ) |
|
|
|
+ (y1 |
+ y2 ) |
|
|
|
+ z2 ) |
|
|
|
|
|
||||||||||||||
|
|
|
a1 |
|
a 2 |
i |
j +(z1 |
k; |
(1.47) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
− |
|
|
= (x1 |
− x 2 ) |
|
|
+ (y1 |
− y2 ) |
|
|
− z2 ) |
|
|
|
|
|||||||||||||||||||
|
|
|
a1 |
|
|
a 2 |
i |
j + (z1 |
k; |
(1.48) |
|||||||||||||||||||||||||||||||
|
|
|
λ |
|
= λ x1 |
|
|
+ λ y1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
a1 |
i |
j + λ z1 k , где λR |
(1.49) |
|||||||||||||||||||||||||||||||||||
ПРИМЕР 1.22 (Условие коллинеарности двух векторов). |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
, если |
|||||||||||||||||||||||||||||||||
Установить условие коллинеарности векторов |
a1 |
и |
a 2 |
||||||||||||||||||||||||||||||||||||||
|
|
= {x1; y1;z1}, |
|
= {x 2 ; y2 ;z2 }. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
a1 |
a 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
45
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= λ |
|
|
, |
где λ − |
||||||||
Решение. |
Так |
как векторы коллинеарны, то |
|
a1 |
a 2 |
||||||||||||||||||||||||||||||||||||||
некоторое число. Согласно (1.46) - (1.49) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x1 |
|
+ y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
i |
j + z1 k = λ x 2 i + λ y2 j + λ z2 k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x = λ x 2 , y1 = λ y2 , z1 = λ z2 |
λ = |
x1 |
= |
y1 |
= |
z1 |
|
(1.50) |
||||||||||||||||||||||||||||||||||
|
x 2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
z2 |
|
||||||||
Легко проверяется, что если координаты векторов удовлетворяют |
|||||||||||||||||||||||||||||||||||||||||||
|
|
= λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
равенствам (1.50), то |
a1 |
a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Равенства (1.50) называются условием коллинеарности двух векторов. |
|||||||||||||||||||||||||||||||||||||||||||
ПРИМЕР 1.23 (Координаты единичного вектора). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 , если |
|
= {x; y;z}. |
|||||||||||||||||||||||||||||||
Определить координаты единичного вектора |
a |
a |
|||||||||||||||||||||||||||||||||||||||||
Решение. |
Согласно формуле (1.33) |
|
= |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
a |
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
a0 = |
1 a = xi + y j + zk |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
a |
x2 + y2 + z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
x 2 + y2 + z2 i + |
x 2 + y2 + z2 j |
+ |
|
|
|
x 2 + y2 + z2 k . |
|
|
|
|
||||||||||||||||||||||||||||||||
Из (1.43) следует, что
a0 = cos αi +cosβj +cos γk = {cosα;cosβ;cos γ}.
Под простейшими задачами аналитической геометрии понимаются задачи определения расстояния между двумя точками и деления некоторого отрезка в данном отношении.
Задача определения расстояния между двумя точками
Пусть в пространстве R 3 |
заданы своими координатами две точки |
|||||||
M1 (x1; y1;z1 ) и M2 |
(x 2 ; y2 ;z2 ). Построим векторы |
|
1, |
|
2 , |
|
|
|
OM |
OM |
M1M2 |
||||||
(рис. 1.16). |
|
|
|
|
|
|
|
|
46

Рис 1.16
.
Тогда OM1 ={x1; y1;z1}, OM2 = {x2 ; y2 ;z2 }, M1M2 = OM2 −OM1
Согласно правилу (1.48) |
|
M1M2 = (x 2 − x1 )i +(y2 − y1 )j +(z2 − z1 )k . |
|
Так как длина вектора M1M2 равна расстоянию между точками M1 и |
|
M2 , то d = M1M2 = (x 2 − x1 )2 +(y2 − y1 )2 +(z2 − z1 )2 |
(1.51) |
Заметим, что в процессе решения этой задачи установлена формула определения координат вектора, если заданы координаты его начальной и
конечной точек: |
|
|
= (x 2 − x1 ) |
|
+(y2 + y1 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
M1M2 |
i |
j + (z2 − z1 )k |
|
|
|
(1.52) |
|||||||||||||||
|
|
|
|
|
|
|
Задача деления отрезка в данном отношении |
|
||||||||||||||||
|
Пусть даны две точки M1 (x1; y1; z1 ) и M2 (x 2 ; y |
2 ; z2 ). Требуется на |
||||||||||||||||||||||
прямой M1M2 |
(рис. 1.17) найти точку |
M0 (x0 ; y0 ; z0 ), которая разделила |
||||||||||||||||||||||
бы отрезок |
[M1M2 ] |
в |
заданном |
отношении |
λ, т.е. |
так, что |
||||||||||||||||||
|
M1M0 |
= λ |
M0M2 |
. Согласно формуле (1.52) |
|
|
|
|
||||||||||||||||
|
|
|
|
|
= {x0 − x1; y0 − y1; z0 − z1}, |
|
|
|
|
|||||||||||||||
|
|
|
M1M0 |
|
|
|
|
|||||||||||||||||
|
|
|
|
= {x 2 − x0 ; y2 − y0 ; z2 − z0 }. |
|
|
|
|
||||||||||||||||
|
|
|
M0M2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
= λ |
|
|
|
|
||||||||||||
|
Тогда по правилу (1.49) равенство |
|
|
M1M0 |
M0M2 |
примет вид |
||||||||||||||||||
|
x0 − x1 = λ (x 2 − x0 ), y0 − y1 = λ (y2 − y0 ), z0 − z1 = λ (z2 − z0 ). |
|||||||||||||||||||||||
|
Определяя x0 , y0 , z0 |
из этих равенств, получим |
|
|
|
|
||||||||||||||||||
|
|
|
x0 = |
x1 + λ x 2 |
, y0 |
= |
y1 + λ y2 |
, z0 = |
z1 + λ z2 |
, |
(1.53) |
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
1+ λ |
|
|
|
1+ λ |
|
|
|
|
|
1+ λ |
|
|
|
|
|||
|
где λ R, λ ≠ −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
47
Рис. 1.17
Формулы (1.53) являются формулами деления отрезка в данном отношении. В частности, при λ = 1 получим формулы деления отрезка пополам:
|
x0 = |
x1 + x 2 |
, y0 |
= |
y1 + y2 |
|
, z0 = |
z1 + z2 |
. |
(1.54) |
|||||||||
|
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||
ПРИМЕР 1.24 |
|
|
Вершины треугольника ABC имеет координаты |
||||||||||||||||
A(2;4;0), B(0;3;5),C(2;5;7) . Найти длину медианы |
AD этого треугольника. |
||||||||||||||||||
Решение. Точка D делит отрезок [BC] пополам. Тогда, согласно формул |
|||||||||||||||||||
(1.54), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x D |
= |
|
x B + xC |
= |
|
0 + 2 |
=1, yD = |
yB + yC |
= |
3 +5 |
= 4, |
||||||||
|
|
2 |
|
|
2 |
||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
|||||||||||
zD |
= |
zB + zC |
|
= |
5 + 7 |
|
= 6. |
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Искомое расстояние найдем по формуле (1.51)
d = AD =  (x D − x A )2 + (yD − yA )2 + (zD − zA )2 =
(x D − x A )2 + (yD − yA )2 + (zD − zA )2 =
= 1+ 0 +36 =
1+ 0 +36 =  37.
37.
1.6.7Скалярное произведение векторов
Пусть даны два вектора a и b . В векторной алгебре рассматриваются два вида умножения векторов: скалярное, результатом которого является число, и векторное, результатом которого является вектор.
ОПРЕДЕЛЕНИЕ 1.36 Скалярным произведением векторов a и b
называется число, равное произведению модулей перемножаемых векторов на косинус угла ϕ между ними (рис.1.18). Скалярное произведение
обозначается символом ab . Итак,
48
|
|
|
|
|
|
|
|
|
|
|
cos ϕ. |
(1.55) |
ab = |
a |
|
b |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.18 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos ϕ = пр |
|
|
|
|
|
|
|
|
|
|
|
cos ϕ = пр |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Так как |
b |
b, |
a |
a, |
|||||||||||||||||||||||||||||||||||
|
|
|
a |
b |
|||||||||||||||||||||||||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ab = |
a |
пр |
|
b = |
b |
пр |
|
a. |
(1.56) |
||||||||||||||||||||||||||||||
a |
b |
||||||||||||||||||||||||||||||||||||||
Из (1.56) следует, что скалярное произведение векторов a и bравно модулю одного из векторов, умноженному на проекцию другого на направление первого вектора.
Свойства скалярного произведения векторов:
1)a b = b a;
2)ab = 0, если a b или хотя бы один из векторов есть нулевой вектор
(справедливо и обратное утверждение);
3)a a = a 2 ;
4)λ(ab) = (λa)b = a(λb) для λ R;
5)(a + b)c = a c + b c.
Справедливость первых четырех свойств непосредственно следует из определения скалярного произведения. Докажем справедливость распределительного свойства 5. Согласно формуле (1.56) и теореме 1.5 о проекции имеем
(a + b)c = c прс (a + b)= c ( прс a + прс b) = c прсa + c прс b = = c a + c b = a c + b c.
Пусть векторы a и b заданы своими координатами: a = x1i + y1 j + z1 k, b = x 2 i + y2 j + z2 k.
Найдем скалярное произведение a b. Вычислим предварительно скалярные произведения единичных векторов.
Имеем ii = i
 i cos 0 =1 1 1 =1, jj =1, kk =1. Векторы i, j,k взаимно
i cos 0 =1 1 1 =1, jj =1, kk =1. Векторы i, j,k взаимно
перпендикулярны. Тогда, согласно свойству 2, их произведения друг на друга равны нулю.
49
Используя распределительный закон скалярного произведения, получим ab = (x1i + y1 j + z1 k)(x 2 i + y2 j + z2 k)= x1x 2 ii + x1y2 i j + x1z2 ik +
+y1x 2 i j + y1y2 jj + y1z2 jk + z1x 2 ki + z1y2 k j + z1z2 kk =
=x1x 2 + y1y2 + z1z2
Итак, если векторы a и b заданы своими координатами, то
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ab = x1x 2 + y1y2 + z1z2 . |
|
|
|
|
(1.57) |
|||||||||||||||||||
Следствие 1. Если |
ϕ = |
π, то |
|
|
|
|
|
|
|
|
|||||||||||||||
ab = 0 или |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1x 2 + y1y2 + z1z2 |
= 0. |
|
|
|
|
|
|
|
|
|
(1.58) |
|||||||||||||
Условие (1.58) называется условием перпендикулярности двух |
|||||||||||||||||||||||||
векторов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следствие 2. Так как |
ab = |
a |
|
b |
cos ϕ,то |
|
|
|
|
|
|||||||||||||||
|
|
ab |
|
|
|
|
|
|
|
|
|
x1x 2 + y1y2 + z1z2 |
|
|
|
|
|||||||||
cos ϕ = a b = |
|
|
x12 + y12 + z12 x 2 |
2 + y2 |
2 + z2 |
2 |
, |
(1.59) |
|||||||||||||||||
ПРИМЕР 1.25 Вычислить работу по перемещению материальной точки вдоль отрезка, из точки B(1;−2;3) в точку С(3;4;2) под действием постоянной
по величине и направлению силы F = {2;1;5}.
Решение. Из курса физики известно, что работа A, совершаемая при |
|
указанных в примере условиях, находится по формуле A = F S = F BC. Так |
|
как BC ={2;6;−1},F ={2;1;5}, то |
|
A = FBC = 2 2 +1 6 +5 (−1) = 5. |
Ответ: 5. |
ПРИМЕР 1.26 Даны вершины треугольника A(−1;−2;4), B(−4;−2;0) и C(3;−2;1) . Определить внутренний угол треугольника при вершине B (рис. 1.19).
|
|
|
|
Рис. 1.19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Имеем |
|
|
Решение. Построим векторы |
BA |
|
и |
BC |
|||
|
|
= {3;0;4}, |
|
= {7;0;1} . Тогда |
|
|
|
|
|
BA |
BC |
|
|
|
|
|
|||
50
