Lab_rab_3

В работе описана методика исследования временных характеристик типовых звеньев. Описан порядок проведения работы, требования к оформлению отчета. Приведены необходимые сведения по динамическим характеристикам звеньев.

Составители: Аязян Г.К., канд. техн. наук., профессор; Хоробров В.Р., доцент, канд. техн. наук

Рецензент: Веревкин А.П., д-р техн. наук, профессор

Уфимский государственный нефтяной технический университет, 1987 Электронная редакция: О.В. Кирюшин, 2002

1. Цель работы.

Целью работы является исследование динамических свойств типовых звеньев автоматических систем регулирования (АСР) и определение параметров звеньев по экспериментальным характеристикам. В процессе работы студент должен закрепить теоретический материал по разделам «Динамические характеристики линейных систем» и «Типовые динамические звенья», уметь определять по виду переходной характеристики уравнения звеньев и их параметры.

2. Описание установки.

Экспериментально-исследовательская часть работы проводится на компьютерах с использованием пакетов «ТАУ», «SIAM», «VisSim» или др.

3. Порядок выполнения работы.

Каждый студент проводит исследование трех типовых звеньев. Типы звеньев, численные значения коэффициентов их уравнений и начальные условия задаются преподавателем из табл. 1.

3.1.Получить индивидуальное задание от преподавателя (см. табл. 1, согласно варианту).

3.2.Подготовить ответы на контрольные вопросы. В процессе подготовки студент должен изучить необходимый для проведения работы теоретический материал. Необходимо знать способы описания динамических свойств линейных звеньев. Уметь по передаточной функции или дифференциальному уравнению определять аналитические выражения временных характеристик, освоить методику качественного анализа переходных характеристик по передаточным функциям. Для проверки готовности в разделе 6 приведены контрольные вопросы.

3.3.Произвести необходимые подготовительные расчеты, необходимые для моделирования заданных звеньев на компьютере.

3.4.В соответствующем пакете имитационного моделирования (по выбору студента) составить расчетные схемы моделей, произвести расчет при заданных начальных условиях, построить переходные кривые.

3.5.Получить аналитические выражения переходных процессов указанных звеньев при нулевых начальных условиях.

3.6.Оформить отчет и защитить работу.

4. Теоретическая часть.

4.1. Способы описания динамических свойств АСР.

Динамические свойства линейного звена или системы могут быть описаны при помощи дифференциальных уравнений (ДУ), передаточных функций, частотных, временных характеристик и т.д.

Продолжение табл. 1

4.1.1 Дифференциальные уравнения.

Как правило, АСР представляет собой соединение нескольких звеньев, каждое из которых может быть описано дифференциальным уравнением. Таким образом, АСР описывается системой линейных дифференциальных уравнений. Исключая промежуточные переменные, можно получить дифференциальные уравнения n-го порядка:

где y(t), x(t) – выходная и входная величины соответственно;

y0 = y(0), y (0i) = y(i) (0) – начальные условия выходной величины и ее про-

изводных.

4.1.2 Передаточная функция.

Динамические свойства линейных звеньев (систем) удобнее описы-

вать передаточной функцией W(s), которая представляет собой отношение изображения по Лапласу выходной величины Y(s) к изображению вход- ной величины X(s) при нулевых начальных условиях, т.е.

∞

где L{f(t)} = ∫f (t)e −pt dt - оператор преобразования Лапласа.

0

Преобразуем по Лапласу обе части уравнения (1) при нулевых начальных условиях, используя теорему о дифференцировании оригинала

откуда в соответствии с формулой (2) получим выражение для передаточной функции:

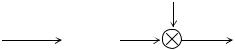
Преобразуя по Лапаласу обе части уравнения (1) с учетом последних

формул, получено:

(an pn + … a1 p + a0) Y(p) – Pн(p) = (bm pm + … + b1 p + b0) X(p), (5) где Pн(p) = an y0pn-1 (an-1 y0 + an y’0) pn-2 + … + (a2 y0 + a3 y’0 + … + an yo(n-2))p +

Слагаемое Fн(р) в уравнении (8) можно рассматривать как изображение некоторого воздействия fн(t), эквивалентного начальным условиям системы и приведенного к выходу (рис. 1).

где первое слагаемое определяет выходной сигнал при нулевых начальных условиях, второе – реакцию на воздействие, эквивалентное начальным условиям. Формулы обратного преобразования Лапласа приведены в Приложении 1. Пример определение выходного сигнала звена, описываемого дифференциальным уравнением с начальными условиями, приведен в Приложении 2.

4.1.3 Временные характеристики.

Динамические свойства систем автоматического управления и их звеньев могут быть однозначно определены временными характеристиками: переходной и импульсной (весовой). Для получения указанных характеристик на вход системы (звена) подают определенного вида воздействие x(t) и исследуют реакцию системы (звена) y(t) на это воздействие (рис. 2).

Рис. 2

Переходной характеристикой системы (звена) h(t) называется ре-

акция звена на единичное ступенчатое воздействие x(t) = 1 (t) при нулевых начальных условиях.

Изображение единичного ступенчатого воздействия по Лапласу рав-

но L{1(t)} = 1 . Изображение переходной функции находится из (9) при p

Замечание. При экспериментальном исследовании динамических характеристик на вход объекта подают скачкообразное воздействие x(t) = A.1(t), где А – амплитуда воздействия. Реакцию объекта на это воздействие иногда называют кривой разгона. Кривая разгона отличается от переходной кривой лишь масштабом.

При x(t) = 1(t) и ненулевых начальных условиях выходной сигнал

Импульсной или весовой характеристикой системы (звена) на импульсное воздействие типа δ-функции при нулевых начальных условиях.

т.е. импульсная характеристика является оригиналом передаточной функции. Известно, что импульсная характеристика равна производной пере-

4.2. Типовые звенья АСР.

Реальные элементы АСР можно аппроксимировать с достаточной степенью точности отдельными типовыми элементарными звеньями или их соединениями.

Типовыми элементарными звеньями принято называть линейные звенья, динамические свойства которых описываются дифференциальными уравнениями не выше второго порядка с постоянными действительными коэффициентами.

В зависимости от свойств все звенья можно разбить на три группы: статические (пропорциональные), дифференцирующие и интегрирующие.

Передаточная функция статических звеньев имеет вид

порционального звена стремится к некоторому пропорциональному значению (рис. 3)

hуст = lim h(t) = W(0) = K .

t →∞

h(t)

t

Рис. 3 Примерами пропорциональных звеньев являются звенья с переда-

точными функциями

Передаточная функция дифференцирующего звена имеет вид: W(p) = pr W1(p), (17)

где r ≥ 1, а W1(p) соответствует пропорциональному звену. Таким образом, W(p) имеет сомножителем pr. Дифференцирующее звено можно получить из передаточной функции (16), если в последней b0 = 1 (r = 1), b0 = b1 = 0 (r = 2) и т.д.

Из (17) следует, что hуст = W(0) = 0.

Примерный вид переходных кривых дифференцирующих звеньев показан на рис. 4.