Композиция двумерных преобразований

Понятие композиции было введено в предыдущем разделе. В данном разделе мы покажем, каким образом можно использовать композицию преобразований для объединения фундаментальных матриц R, S и Τ с целью получения желаемых общих результатов. Основное преимущество объединенных преобразований состоит в том, что к точке более эффективно применять одно результирующее преобразование, чем ряд преобразований друг за другом.

Рассмотрим, например, поворот объекта относительно некоторой произвольной точки Pi. Поскольку нам известно, лишь как поворачивать вокруг начала координат, разобьем исходную (трудную) проблему на три более легкие задачи. Таким образом, чтобы произвести поворот относительно точкиPi, необходимо выполнить последовательно три элементарных преобразования:

1. Перенос, при котором точка Pi перемещается в начало координат.

2. Поворот.

3. Перенос, при котором точка из начала координат возвращается в первоначальное положение Ρi.

Эта последовательность показана на рис. 2.3, на котором вокруг точки Ρi(x, у) поворачивается контур домика. Первый перенос производится на(-x₁, -y₁),в то время как последующий — на (x₁, y₁) — является обратным ему. Результат существенно отличается от того, который получился бы, если бы применялся один только поворот.

Результирующее преобразование имеет вид

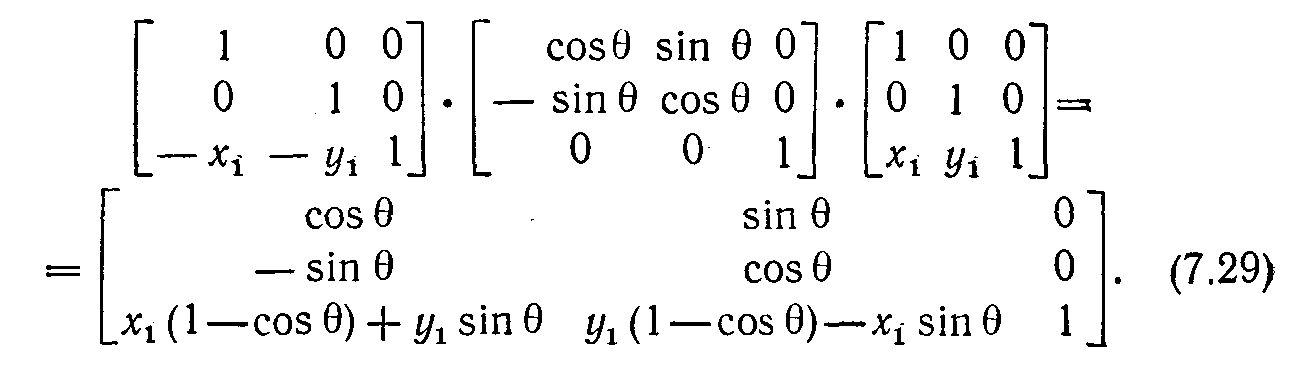
Эта композиция преобразований путем умножения матриц служит примером того, как применение однородных координат упрощает задачу.

Используя аналогичный подход, можно промасштабировать объект относительно произвольной точки Рi: перенестиΡi в начало координат, промасштабировать, перенести назад в точкуΡi. Результирующее преобразование в этом случае будет иметь вид

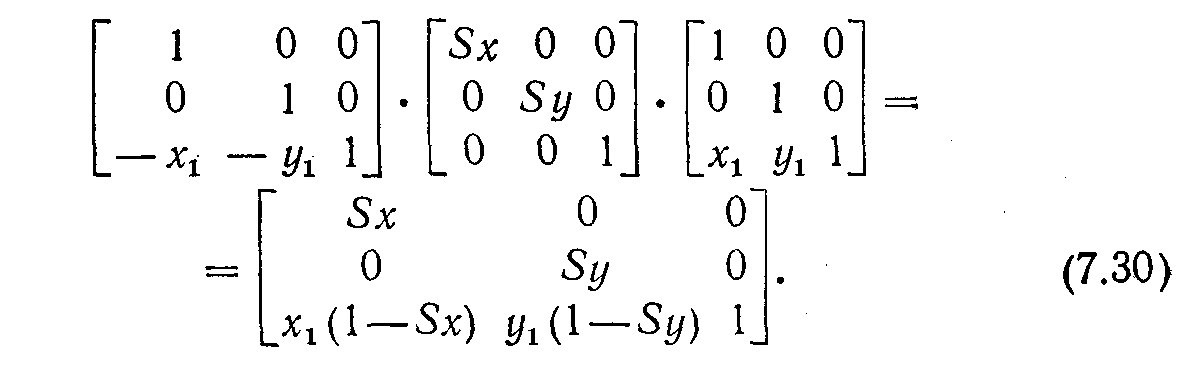
Предположим, что нам необходимо промасштабировать, повернуть и расположить в нужном месте домик, показанный на рис.2.3, где центром поворота и масштабирования является точка Ρ₁. Последовательность преобразований заключается в переносе точкиΡ₁ в начало координат, проведении масштабирования и поворота, а затем переносе из начала координат в новую позицию Р₂, в которой домик должен оказаться (эта последовательность показана на рис. 2.3). В структуре данных, в которой содержится это преобразование, могут находиться масштабный множитель (множители), угол поворота и величины переноса или может быть записана матрица результирующего преобразования:

Если известно, что M₁ иM₂представляют собой элементарные перенос, масштабирование или поворот, то при каких условияхΜ₁ иΜ₂ коммутативны? В общем случае умножение матриц некоммутативно. Однако легко показать, что в следующих частных случаях коммутативность имеет место (в этих случаях можно не беспокоиться о порядке перемножения матриц – см. Таблицу 2.1).

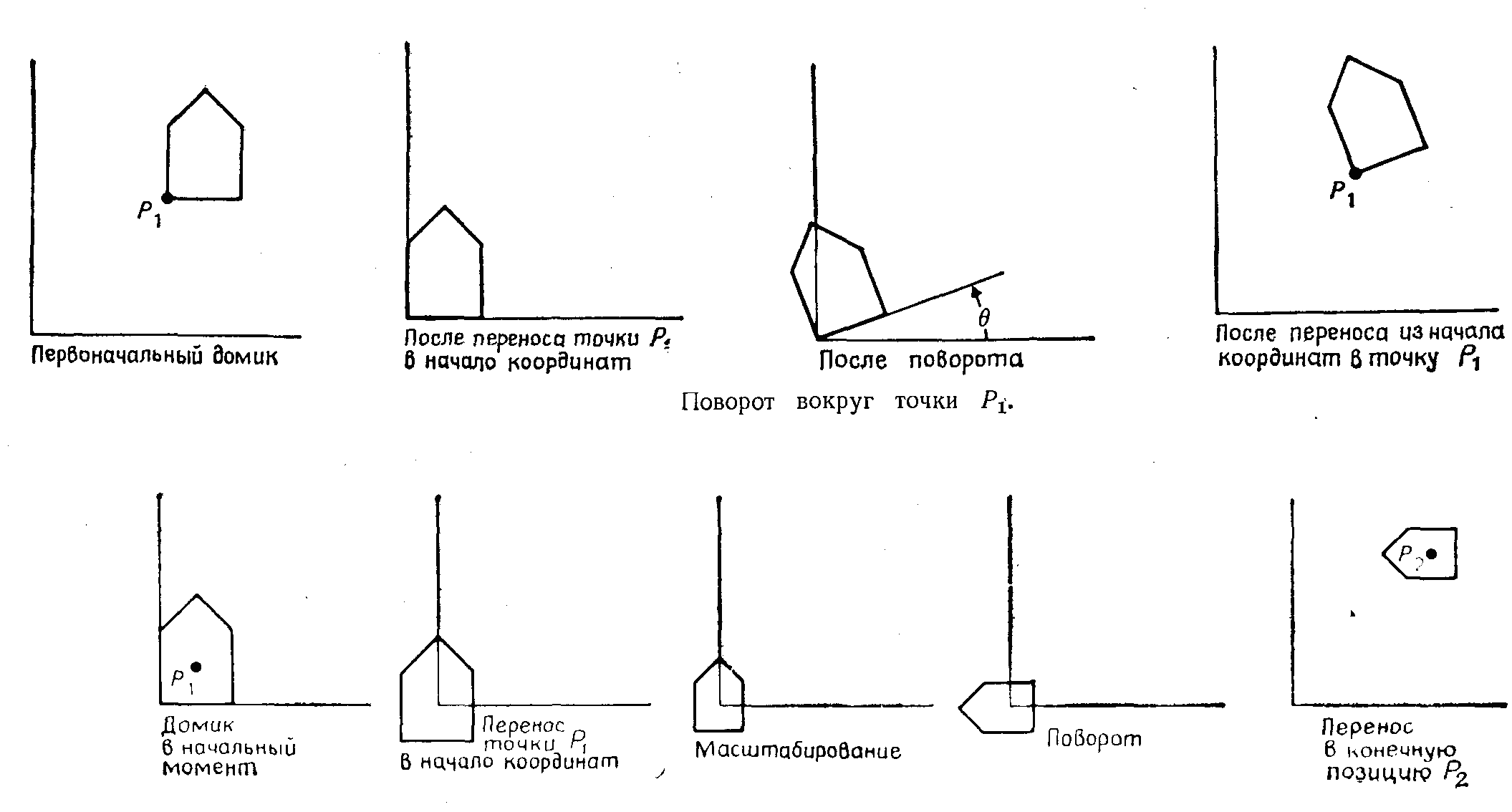
Рис. 2.3 Композиция преобразований

Таблица 2.1

M1	М2
Перенос	Перенос
Масштабирование	Масштабирование
Поворот	Поворот
Масштабирование (при Sx = Sy)	Поворот

Матричное представление трехмерных преобразований

Аналогично тому, как двумерные преобразования описываются матрицами размером 3x3, трехмерные преобразования могут быть представлены в виде матриц размером 4x4. И тогда трехмерная точка (x,у, z) записывается в однородных координатах как(W∙x, W∙y, W∙z, W), гдеW≠0. ЕслиW≠1, для получения трехмерных декартовых координат точки(х, у, z) первые три однородные координаты делятся наW. Отсюда, в частности, следует, что две точкиΗ₁ иH₂в пространстве однородных координат описывают одну и ту же точку трехмерного пространства в том и только в том случае, когдаH₁=cH₂ для любой константыс, не равной нулю.

Трехмерная система координат, применяемая в этой книге, является правосторонней (рис.2.4). Примем соглашение, в соответствии с которым положительными будем считать такие повороты, при которых (если смотреть с конца положительной полуоси в направлении начала координат)поворот на 90° против часовой стрелки будет переводить одну положительную полуось в другую. На основе этого соглашения строится следующая таблица, которую можно использовать как для правых, так и для левых систем координат:

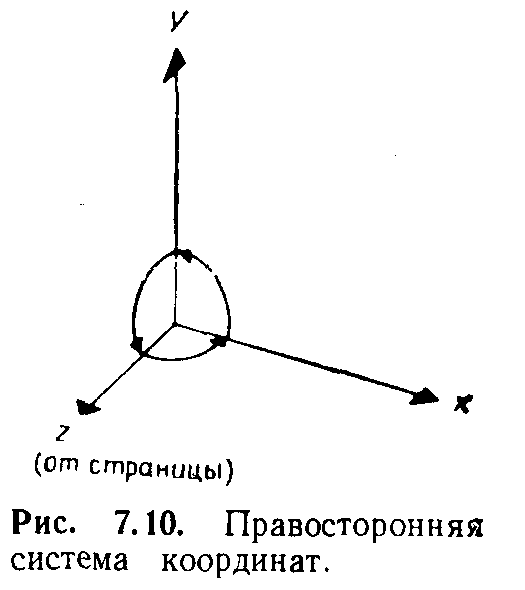
Рис. 2.4. Правосторонняя система координат

Таблица 2.2. Правосторонняя система координат

Если ось вращения	Положительным будет направление поворота
x у z	от у к z от zкx от xкy

Мы применяем здесь правостороннюю систему координат, поскольку она хорошо знакома большинству людей, хотя в трехмерной графике чаще более удобна левосторонняя система, так как ее легче представить наложенной на поверхность экрана дисплея. Это позволяет естественно интерпретировать тот факт, что точки с большими значениями zнаходятся дальше от наблюдателя. Отметим, что в левосторонней системе положительными будут повороты,выполняемые по часовой стрелке, если смотреть с конца положительной полуоси в направлении начала координат.

Трехмерный перенос является простым расширением двумерного:

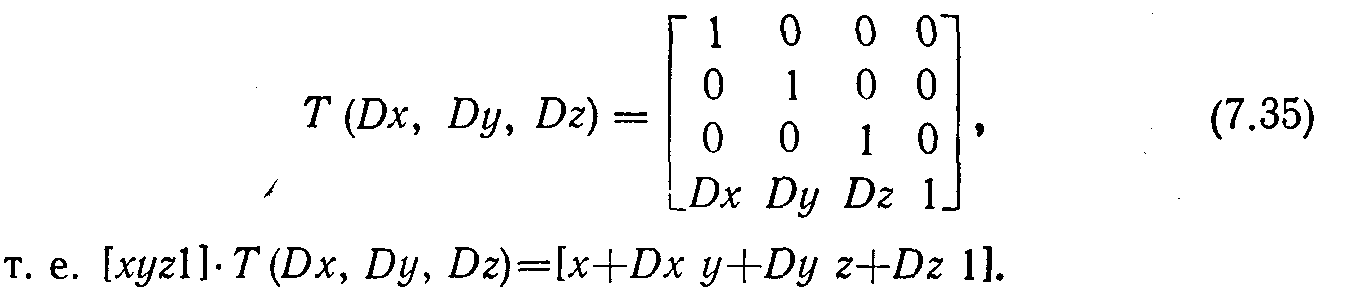
Масштабирование расширяется аналогичным образом:

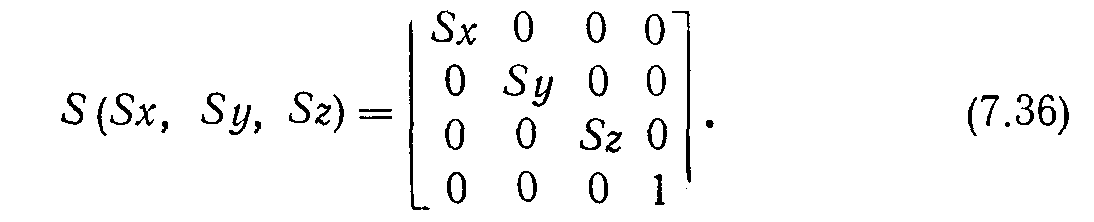
В самом деле,

Двумерный поворот является в то же время трехмерным поворотом вокруг оси z. В трехмерном пространстве поворот вокруг осиz описывается выражением

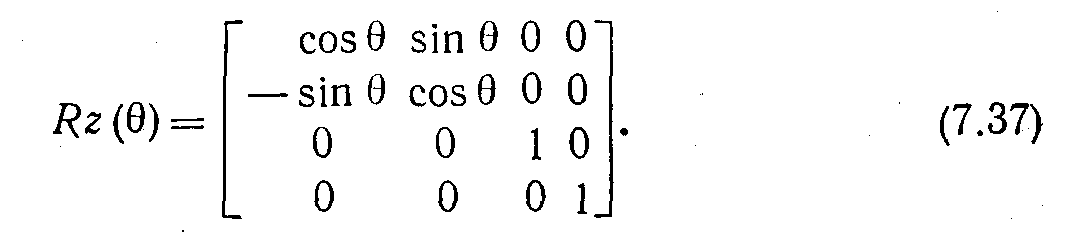
Это легко проверить: в результате поворота на 90° вектора [1 0 0 1], являющегося единичным вектором оси х, должен получиться единичный вектор [0 1 0 1] осиy. Вычисляя произведение

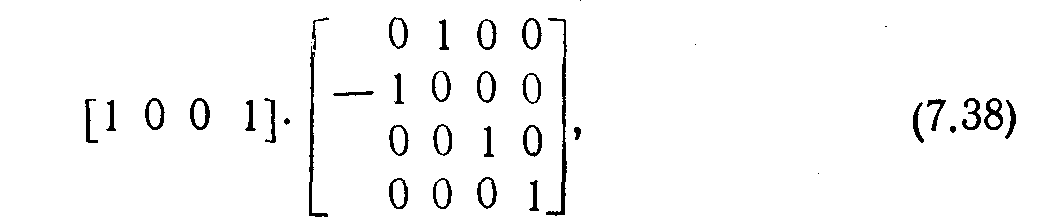
получаем предсказанный результат [0 1 0 1]. Матрица поворота вокруг оси x имеет вид

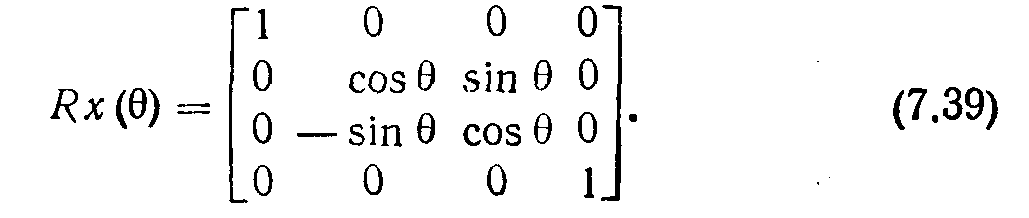
Матрица поворота вокруг оси у записывается в виде

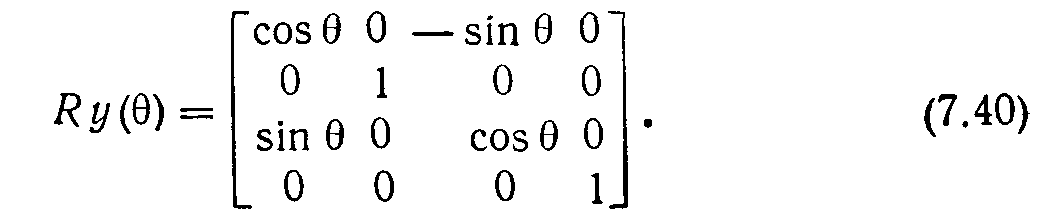
Столбцы (и строки) верхней левой подматрицы размером 3x3 матриц Rz, RxиRyпредставляют собой взаимно ортогональные единичные векторы, интерпретация которых такая же, что и в двумерном случае.

Все эти матрицы преобразований имеют обратные матрицы. Матрица, обратная Т, получается подстановкой знака минус передDx, Dy иDz; обратнаяS— заменойSx, Sy иSz на обратные им значения, а для каждой из трех матриц поворота — выбором отрицательного угла поворота.