Лабораторный практикум по механике

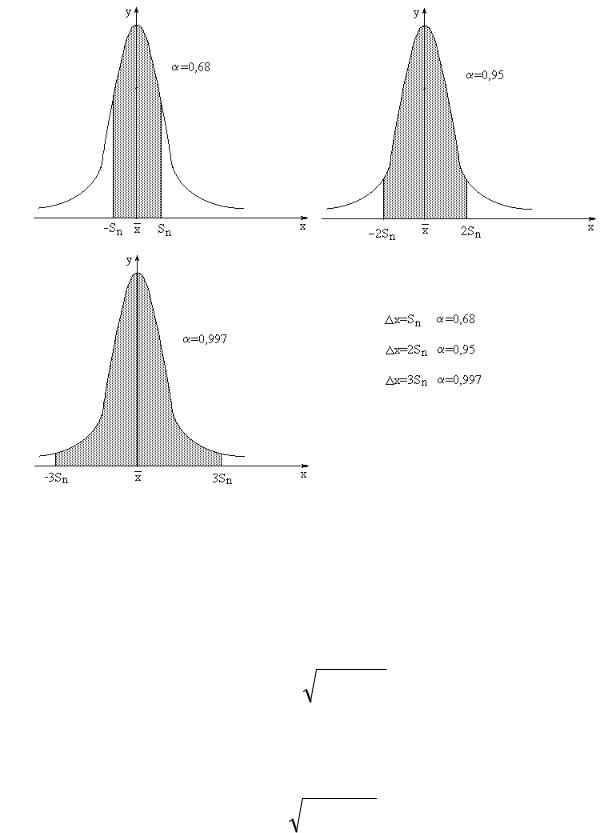
Рис. 2

8. Закон сложения случайных ошибок

Если измеряемая величина z является суммой (или разностью) двух величин X и Y, результаты измерений которых независимы, тогда дисперсии Sz этих величин связаны соотношением

Sz2 = Sx2 + Sy2

или

т.е. средняя квадратичная ошибка суммы (или разности) двух (или нескольких величин) независимых величин равна корню квадратному из суммы дисперсий отдельных слагаемых. Для средних арифметических ошибок закон сложения будет тот же самый:

Из закона сложения ошибок следуют два чрезвычайно важных вывода:

а) значение отдельных ошибок очень быстро падает по мере их уменьшения. Этот вывод всегда нужно иметь в виду, и при повышении точности измерений в первую очередь уменьшать ошибку, имеющую большую величину;

11

б) средняя квадратичная погрешность среднего арифметического равна средней квадратичной погрешности отдельного результата, деленной на корень квадратный из числа измерений:

Это фундаментальный закон возрастания точности при росте числа наблюдений. Разумеется, это рассуждение относится лишь к измерениям, при которых точность результата полностью определяется случайной ошибкой.

9. Определение доверительного интервала и доверительной вероятно-

сти

Очевидно, важнее знать, насколько может уклоняться от истинного значе-

Тогда для аргумента ε, который используется в табл. 1, справедлива зависимость

При применении формул (8) и (9) считается известной средняя квадратичная погрешность σ. Однако, для того чтобы определить последнюю, нужно сделать очень много измерений, что не всегда возможно и удобно. В тех случаях, когда выполняются измерения с помощью уже хорошо исследованного ме-

тода, ошибки которого известны, то заранее известна и величина σ. Но, как правило, погрешность метода приходится определять в процессе измерений. Обычно можно определить только величину Sn, соответствующую сравнительно небольшому числу измерений (см. формулу (3)). Если для оценки доверительной вероятности α считать, что Sn совпадает с σ, и пользоваться табл. 1, то получаются неверные значения α.

Из формулы (14) видно, что tα,n – величина, аналогичная ε: она играет ту же роль, но в случае, когда число измерений, из которых определена ошибка Sn, не очень велико. Величины tα,n, носящие название коэффициента Стьюдента, вычислены для различных значений n и α и приведены в табл. 2 (Прил. 5)

12

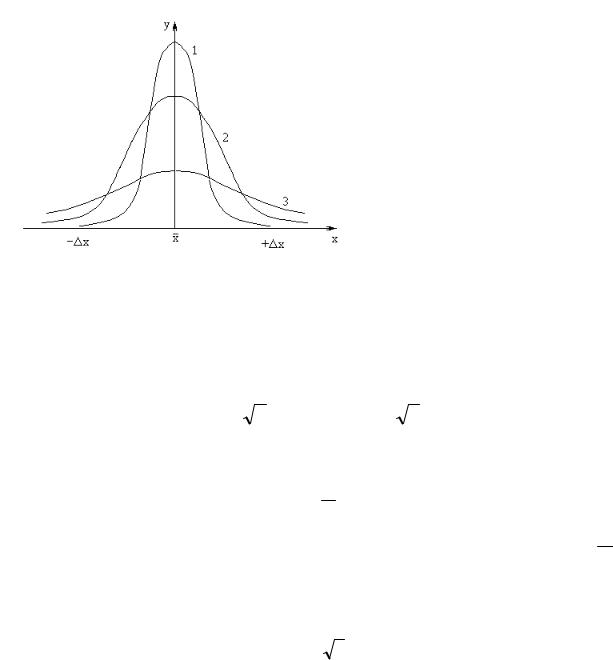
Рис. 3

Сравнивая приведенные в ней данные с табл. 1, легко убедиться, что при больших n величины tα,n стремятся к соответствующим значениям ε. С увеличением n Sn стремится к σ. Используя коэффициенты Стьюдента, равенство (8) можно переписать в виде:

Пользуясь этим соотношением и табл. 2, легко определить доверительные интервалы и доверительные вероятности при любом небольшом числе измерений.

Пример. Среднее арифметическое X из 5 измерений равно 31.2. Средняя квадратичная ошибка, определенная из этих 5 измерений, равна 0.24. Найти до-

верительную вероятность того, что x отличается от истинного значения X не более чем на 0.2, так как будет выполняться неравенство

31 < x < 31.4.

Значение tα,n найдем, подставив наши величины в формулу (15):

По табл. 2 (Прил. 5) находим для n = 5 при tα,n = 1.5 , α= 0.8; при tα,n = 2.1, α = 0,9. Вообще говоря, можно удовлетвориться ответом, что доверительная

вероятность для этого случая лежит между 0.8 и 0.9. Если получить более точное значение, применяют метод интерполяции. В рассматриваемом примере

получается α = 0.86.

10. Погрешность определения погрешности

Если средняя квадратичная ошибка Sn определяется из очень большого числа измерений, то получается величина, как угодно мало отличающаяся от своего предельного значения σ. Но когда n невелико, то Sn отягчена случайными погрешностями. Для определения доверительного интервала, в котором на-

13

ходится σ при заданной доверительной вероятности α, пользуются табл.3 в соответствии с алгоритмом

Приведем два примера пользования табл. 3.

1.Средняя квадратичная погрешность, определенная из 5 измерений, равна

2.Нужно вычислить доверительный интервал для σ c надежностью 0,95.

Из табл. 3 имеем для n = 5 и α = 0.95, γ1 = 0.599 и γ2 = 2.87. Для σ можно записать неравенство, выполняемое с вероятностью 0.95.

0.599 . 2 < σ < 2.87 . 2 или 1.2 < σ < 5.7. 2. При 40 измерениях γ1 = 0.821, γ2 = 1.28

1.6 < σ < 2.6.

По сравнению с первым случаем здесь интервал значительно ýже и почти симметричный.

11. Необходимое число измерений

Для уменьшения случайной ошибки результата могут быть использованы 2

пути: улучшение точности измерений, т.е. уменьшение σ, и увеличение числа измерений, т.е. использование соотношения, аналогичного (12):

Предположим, что все возможности совершенствования техники (т.е. первый путь) измерений уже использованы. Пусть систематическая ошибка изме-

рений равна δ. Известно, что уменьшать случайную ошибку целесообразно до тех пор, пока общая погрешность измерений не будет полностью определяться систематической ошибкой. Практически должно выполняться требование

где x – половина доверительного интервала для величины σ. Надежность α, с которой требуется установить доверительный интервал, в большинстве случаев не должна превышать 0.95. Для оценки необходимого числа измерений приве-

дена табл. 4 (Прил. 5), в которой x дано в долях средней квадратичной ошибки.

Пример. Измеряется напряжение с помощью вольтметра, имеющего погрешность в I В. Средняя квадратичная погрешность измерений равна 2.3 В. Сколько измерений нужно проделать, чтобы получить ошибку не более 1.5 В. с надежностью 0.95?

Положим:

из табл. 4 находим в колонке α = 0.95 : для ε = 0.3 n=46 и для ε = 0.2 n = 99. Методом интерполяции определяем, что для

12. Обнаружение промахов

Если осуществляется ряд одинаковых измерений, подверженных случайным ошибкам, то в этом ряду могут встретиться измерения с очень большими случайными ошибками. Однако большие ошибки имеют малую вероятность, и если среди результатов измерений встретится одно, имеющее резко отличное от других значение, то мы будем склонны приписать такой результат промаху и отбросить его как заведомо неверный. Естественно, следует объективно оценить, является ли данное измерение промахом или же результатом случайного, но совершенно закономерного отклонения.

Для оценки вероятности β случайного появления выскакивающих значений в ряду n измерений (для n < 25) на основании результатов, даваемых теорией вероятностей, была составлена табл. 5 (Прил. 5). При пользовании этой таб-

лицей вычисляется среднее арифметическое X и средняя квадратичная погрешность Sn всех измерений, включая подозреваемое хk, которое, на наш взгляд, недопустимо велико или мало.

Вычисляется относительное уклонение этого измерения от среднего арифметического, выраженное в долях средней квадратичной ошибки

По табл. 5 (Прил. 5) можно определить, какой вероятности β соответствует полученное значение ϑmax. Разумеется, следует договориться, при каких значениях β будет отбрасываться (считаться промахом) измерение. Табл. 5 (Прил. 5) составлена так, что наименьшее значение β = 0.01. Оставлять измерения, вероятность появления которых меньше этой величины, обычно нецелесообразно.

Пример. Среднее арифметическое значение измеряемой величины, полученное из 15 измерений, равно 257.1, среднее квадратичное значение Sn = 2.6. Определить, является ли промахом одно из измерений, равное 266.0. Определяем:

ϑmax = 266 − 257.1 = 3.42 . 2.6

Наибольшее значение ϑmax для n = 15, приведенное в табл. 5, равно 2.8, чему соответствует β = 0.01. Так как с ростом ϑmax соответствующее значение β уменьшается, то при ϑmax = 3.42 должно быть значительно меньше 0.01. Из того, что β << 0.01, следует, что результат 266 надо отбросить, считая его промахом.

Если вероятность появления данного измерения в ряду лежит в промежутке 0.1 > β> 0.01, то представляется одинаково правильным оставить это измере-

15

ние или отбросить. Решая вопрос об отбрасывании выскакивающего измерения, полезно посмотреть, как сильно оно меняет окончательный результат.

В тех случаях, когда β выходит за указанные пределы, вопрос об отбрасывании решается просто.

При n, большем 25, оценку β можно производить с помощью соотношения:

β ≈ (1 – α)n. (19)

Здесь α – доверительная вероятность, определяемая для нормального рас-

пределения (α берется из табл. 1, полагая Sn = σ).

Учет систематической и случайной ошибки. Измерения следует прово-

дить так, чтобы погрешность результата целиком определялась систематической ошибкой измерений, которая обычно задается погрешностью измерительного прибора. Для этого следует определенным образом выбирать необходимое число измерений. Однако не всегда это удается сделать. В результате часто приходится мириться с положением, когда систематическая и случайная ошибки измерений близки друг к другу, и они обе в одинаковой степени определяют точность результата. При этом качестве верхней границы суммарной ошибки можно принять значение

где δ – систематическая ошибка, σ – среднеквадратичная ошибка. Данная оценка верна с вероятностью не менее 0.95.

13. Правила обработки результатов измерений

Указанные правила можно применять для случаев нормального распределения результатов или мало отличающихся от него.

1. Определяют среднее арифметическое значение измеряемой величины:

x = 1 n xi .

n i=1

2. Находят абсолютные погрешности отдельных измерений:

xi = x − xi .

3. Вычисляют среднюю абсолютную погрешность отдельных измерений:

4. Вычисляют среднюю квадратичную погрешность отдельных измерений: Sn = 1.253 x

n

( xi )2

5.Отбрасывают промахи, если x > 3Sn. Повторяют пункт (1-5).

6.Определяют среднюю квадратичную погрешность среднего значения:

16

7.По числу наблюдений n и выбранной вероятности α по табл. 2 сами определяют коэффициент Стьюдента tα,n.

8.Записывают величину доверительного интервала от среднего значения измеряемой величины :

9.Записывают результат измерений:

x= x ± x.

10.Определяют относительную погрешность:

ε = xx 100% .

Примечание. При малом числе наблюдений нужно пользоваться средней квадратичной погрешностью, для которой в этом случае легко определить доверительную вероятность, пользуясь таблицами коэффициентов Стьюдента. При большом числе измерений можно пользоваться средней арифметической или средней квадратичной погрешностью:

x = 0.8Sn .

Пример. Определить доверительный интервал с соответствующей доверительной вероятностью для дальности полета снаряда по следующим результа-

там опыта: 101.5; 105.0; 95.0; 98.5; 100.0 см.

1.x = xi ; X=100 см. n

2.Таблица абсолютных погрешностей.

x = Sntα ,n = 1.7 × 3.75 = 6 .

Следовательно, на 98% можно ручаться, что рассеивание снарядов будет не больше ± 6 см от дальности полета в 100.0 см.

x = 100 ± 6 (см).

14. Обработка результатов прямых измерений

Задание. Измерение линейных размеров тела (длины).

1. Выполните n измерений длины тела и запишите их результаты в табл. 1. Таблица 1

xi

xi

x2i

2.Произведите обработку результатов измерений, выполняя пункты 1-10 параграфа 12.

3.Определите необходимое число измерений для доверительной вероятно-

сти α1 = 0.95 и α2 = 0.9 и средней квадратичной ошибки Sn при X i = X и

X 2 = X стат. по табл. 4 (Прил. 5).

4. Определите доверительный интервал для Sn по формуле 16 при α = 0.95. 5. Определите доверительную вероятность α для интервала x = x по

формуле 14.

6. Запись окончательного ответа X = X + X при доверительной вероятно-

сти α = 0.95.

7. Постройте гистограмму результатов измерений длины тела, используя данные компьютерной обработки.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Типы ошибок.

2.Охарактеризовать 3 группы систематических ошибок.

3.В каких случаях измерение производится один раз, а в каких несколько

раз?

4. Чем определяется необходимое число измерений?

18

5. Какие предположения приводят к Гауссову закону распределения оши-

бок?

6.Средняя квадратичная и средняя арифметическая ошибки.

7.Какие два числа характеризуют величину случайной ошибки?

8.Правила пользования табл. 1.

9.Закон сложения случайных ошибок.

10.Чему равна средняя квадратичная погрешность среднего арифметиче-

ского?

11.Порядок определения доверительных интервалов и доверительных вероятностей при любом небольшом числе измерений.

12.Как определяется доверительный интервал, внутри которого находится

σ?

13.Назначение табл. 4 и правила пользования ею.

14.Правило обнаружения промахов.

15.Оценка результирующей ошибки, когда систематическая и случайная ошибки измерений близки друг к другу.

16.Правило определения точности вычислений.

Литература

1.Касандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. М.:

Наука, 1970.

2.Зайдель А.Н. Элементарные оценки ошибок измерений. М.: Наука, 1967.

3.Щиголев Б.Н. Математическая обработка наблюдений. М.: Физматгиз,

1962.

ЛАБОРАТОРНАЯ РАБОТА 2

ОЦЕНКА ТОЧНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ ПРОВОДНИКА

Цель работы:

1.Ознакомиться с методами оценки результатов косвенных измерений и расчета погрешностей.

2.Определить удельное сопротивление провода и интервал погрешности измерения.

Оборудование: установка (FPM-01) для определения удельного сопротивления проволоки, штангенциркуль, микрометр, проволока.

Краткая теория

В большинстве случаев измеряется не непосредственно интересующая величина Y, а другая - X, зависящие друг от друга тем или иным образом. При таких измерениях, называемых косвенными, необходимо также уметь вычислять ошибку измерений.

19

Первый способ:

1. Величина Y зависит от одной измеряемой величины X. Y = f(x)

Если Y = f(x), то, когда ошибки малы по сравнению с измеряемой величиной, можно записать

2. Пусть x является некоторой функцией y и z, т.е. x = f(y,z).

Тогда наилучшее значение при оценке x равно

x = f( y, z).

Погрешности косвенных измерений x определяют как приращение функ-

ции f(y,z):

Более точным является выражение:

Второй способ:

На практике при вычислении погрешностей косвенных измерений удобнее сразу вычислить относительную погрешность по правилу дифференцирования натурального логарифма функции.

Прологарифмируем правую и левую часть функции Y = f(x, z): ln y = ln x + ln z.

Продифференцируем правую и левую часть: (ln y)`= (ln x)` + (ln z).

Пример вычисления погрешностей при косвенных измерениях удельного сопротивления проводника

Пусть электрическое сопротивление участка однородного линейного проводника

где R – сопротивление отрезка проводника, L – его длина, S – площадь поперечного сечения, ρ – удельное сопротивление проволоки. Отсюда:

ρ = R SL .

Для измерения сопротивления с использованием закона Ома собирают электрическую цепь (см. рис. 1). Участок цепи АВ – отрезок проволоки, Е – источник тока, А – амперметр, V – вольтметр. Чтобы определить ρ, необходимо

20