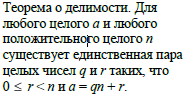вопросы

вопросы

ответы

задачи

1

Решите уравнение 3x + 5y = 7 в целых числах.

Решение:

Найдем сначала какое-нибудь конкретное решение (эта идея, кстати, часто помогает и при решении других задач). Так как 3 • 2 + 5 • ( – 1) = 1, то 3 • 14 + 5 • ( – 7) = 7 и, следовательно, x₀ = 14, y₀ =  – 7 – это решение нашего уравнения (одно из многих, не более!). Итак,

Вычтем одно уравнение из другого, обозначим x – x₀ и y – y₀ через a и b, и получим 3a + 5b = 0. Отсюда мы видим, что b делится на 3, а a – на 5. Положим a = 5k, тогда b =  – 3k – здесь k, очевидно, может быть любым целым числом. Итак, мы получаем набор решений:

где k может быть любым целым числом. Других решений, конечно, нет.

2

Найдите все целые решения уравнения 21x + 48y = 6.

Решение:

x = 16k – 2, y =  – 7k + 1; k – любое целое число.

3

Задачи такого типа решаются так: 7^1 заканчивается на 7 7^2 заканчивается на 9 7^3 заканчивается на 3 7^4 заканчивается на 1 7^5 заканчивается на 7 Т.е видно, что цифры 7, 9,3,1 циклически повторяются. Теперь делим 777 на 4 с остатком. Остаток =1, значит попследняя цифра - 7.

4

3/7=0 остаток 3 9/7=1 остаток 2 27/7=3 остаток 6 81/7=11 остаток 4 243/7=остаток 5 729/7=104 остаток 1 Остатки образуют ряд чисел из повторяющейся послед-ности 3 2 6 4 5 1 Цикл состоит из 6 делений значит 1989/6=331 остаток три, смотрим третью строку , в третьей строке остаток 6, значит остаток от деления 3^1989 на 7 = 6

5

Теорема о делимости

Для любого а и любого ненулевого n существуют единственные (целые) частное q и

остаток r, такие, что а = nq + r, 0 <= r < |n|.

Доказательство.

Рассмотрим множество целых чисел вида

а — kn,

где k пробегает все множество целых чисел, положительных и неположительных; т.е. рассмотрим прогрессию

... , а - 3n, а - 2n, а - n, a, a + n, a + 2n, а + 3n,....

Выберем в этой последовательности наименьшее неотрицательное число и обозначим его r, и пусть q обозначает соответствующее значение k. (Такое r существует, потому что множество

{а — кn} содержит отрицательные и неотрицательные значения, а из полной упорядоченности следует, что непустое множество неотрицательных целых чисел содержит наименьший элемент.) По определению

r = а — qn >= 0.

Для доказательства единственности допустим, что

a=nq1+r1, 0<=r1<|n|

и что r1 не = r.

Пусть для определенности r1 < r, так что 0 < r - r1 < |n|; тогда

r - r1 = (q1 - q)n и n|(r — r1), что противоречит неравенствам 0 < r - r1 < |n|

6

Теорема

Если а и b — произвольные целые числа, отличные от нуля, то величина НОД (а, b) равна наименьшему положительному элементу множества {ах + by : х,уZ} линейных комбинаций чисел а и b.

Доказательство.

Обозначим через s наименьшую положительную из таких линейных комбинаций чисел а и b, и пусть s = ах + by при некоторых х, у Z.

Пусть также q = [a/s]. Тогда из равенства a mod n = a – [a/n]n следует

a mod s = a — qs = а — q (ах + by) = а (1 — qх) + b (—qy) ,

поэтому величина a mod s также является линейной комбинацией чисел а и b.

Но поскольку 0 <= a mod s < s, выполняется соотношение а mod s = 0, так как s — наименьшая положительная из таких линейных комбинаций. Поэтому s|а; аналогично можно доказать, что s|b. Таким образом, s — общий делитель чисел а и b, поэтому справедливо неравенство НОД (а, b) >= s. Из уравнения d|a и d|b следует d|(ax+by) следует, что НОД (a, b)|s, поскольку величина НОД (a, b) делит и а, и b, a s — линейная комбинация чисел а и b. Но из того, что НОД (а, b) | s, и s > 0 следует соотношение НОД (а, b) <= s. Совместное применение неравенств НОД (a, b) <= s и НОД (а, b) >= s доказывает справедливость равенства НОД (a, b) = s; следовательно, можно сделать вывод, что s — наибольший общий делитель чисел а и b.

7

Теорема 1.

Для любых целых чисел а и b из соотношений d|а и d|b следуете d | НОД (а, b).

Доказательство.

Это следствие является результатом уравнения d|a и d|b следует d|(ax+by) поскольку, согласно теореме (билет 6), величина НОД (а, 6) является линейной комбинацией чисел а и b.

Теорема 2.

Для любых целых чисел а и b и произвольного неотрицательного целого числа n справедливо соотношение

НОД (an, bn) = п НОД (a, b) .

Доказательство.

Если n = 0, то следствие доказывается тривиально. Если же n > 0, то НОД (an, bn) — наименьший положительный элемент множества {аnх+bnу}, в n раз превышающий наименьший положительный элемент множества {ах + by}.

8

Теорема 1.

Для всех положительных целых чисел n, а и b из условий n|ab и НОД (a, n) = 1 следует соотношение n |b.

Доказательство. нет

Теорема 2.

Для любых целых чисел a, b и р из соотношений НОД (a,p) = 1 и НОД (b,р) = 1 следует соотношение НОД (ab,p) = 1.

Доказательство.

Из теоремы (билет 6) следует, что существуют такие целые числа х, у, х'и у' для которых

ах+ру = 1,

bх'+ ру' = 1.

Умножив эти уравнения друг на друга и перегруппировав слагаемые, получим:

аb (х x') + р (ybx' + у'ах + руу') = 1.

Поскольку положительная линейная комбинация чисел аb и р равна 1, применение

теоремы (билет 6) завершает доказательство.

9

Теорема 1.

Для любого простого числа р и всех целых чисел а и b из условия р|аb следуют либо соотношение р | а, либо соотношение р | b, либо они оба.

Доказательство.

Проведем доказательство методом "от противного". Предположим, что р|аb, но р не|а и р не|b. Таким образом, НОД (а, р) = 1 и НОД (b, р)= 1, поскольку единственными делителями числа р являются 1 и р, и, согласно предположению, на р не делится ни а, ни b. Тогда из теоремы (билет 8) следует, что НОД (ab,p) = 1, а это противоречит условию, что р | ab, поскольку из него следует,

что НОД (ab, р) = р. Это противоречие и служит доказательством теоремы.

Теорема 2.(Единственность разложения на множители).

Целое составное число а можно единственным образом представить как произведение вида а =

= где - простые числа, р1 < Р2 < … < , а ei — целые положительные числа.

Доказательство.

10

Теорема. (Рекурсивная теорема о НОД)

Для любого неотрицательного целого числа а и любого положительного целого числа b справедливо соотношение НОД (a, b) = НОД (b, а mod b).

Доказательство.

Покажем, что величины НОД (a, b) и НОД (b, a mod b) делятся друг на друга, поэтому они должны быть равны друг другу (поскольку оба они неотрицательны) согласно уравнению (из а | b и b | а следует а = ±b).

Сначала покажем, что НОД (а, b) | НОД(b, а mod b). Если d = НОД (а, b), то d | a и d | b. Согласно уравнению (a mod n = а — [a/n] n), (a mod b) = а — qb, где <q = [a/b]. Поскольку величина (a mod b) представляет собой линейную комбинацию чисел а и b, то из уравнения (из d | а и d | b следует d|(ах + by)) следует, что d | (a mod b). Таким образом, поскольку d|b и d|(a mod b), согласно следствию (Для любых целых чисел а и b из соотношений d | а и d | b следуете d| НОД (а, b)), d|НОД (b, a mod b) или, что то же самое, НОД (a, b) | НОД (b, a mod b).

Соотношение НОД (b, а mod b) | НОД (а, b) доказывается почти так же. Если ввести обозначение d=НОД (b, a mod b), то d|b и d|(a mod b). Поскольку а = qb + (а mod b), где q = [a/b], a представляет собой линейную комбинацию величин b и (a mod b). Согласно уравнению (из d|а и d|b следует d|(ах + by)), можно сделать вывод, что d|а.

Поскольку d|b и d|a, то, согласно следствию (Для любых целых чисел а и b из соотношений d|а и d|b ) следует d|НОД (а, b)), справедливо соотношение d|НОД(a, b) или эквивалентное ему НОД(b,a mod b)| НОД (a, b).

11

УсловиеДокажите, что n3 – n делится на 24 при любом нечетном n. ПодсказкаДокажите, что указанное число делится и на 3, и на 8. Решениеn3 – n = (n – 1)(n + 1). Из трёх последовательных чисел одно делится на 3. n – 1 и n + 1 – последовательные четные числа. Поэтому одно из них не только чётно, но и делится на 4. Значит, всё произведение делится на 2·4·3 = 24.

12

Группа (group) S, ) — это множество S, для элементов которого определена бинарная операция обладающая перечисленными ниже свойствами.

1. Замкнутость: для всех элементов a,b S имеем a b S.

2. Существование единицы: существует элемент е S, который называется единичным (identity) элементом группы; для этого элемента и любого элемента а S выполняется соотношение

Е a=а е=а.

3. Ассоциативность: для всех a,b,c S выполняется соотношение (а b) с = а (b с).

4. Существование обратного элемента: для каждого элемента а S существует единственный элемент b S (он называется обратным (inverse) к элементу а), такой что а b = b а = е.

В качестве примера рассмотрим уже знакомую нам группу (Z, +) целых чисел с операцией сложения: в ней единичный элемент — 0, а обратный элемент к любому числу а — число —а. Если группа S, ) обладает свойством коммутативности (commutative law) а b = b а для всех а, b S, то это абелева группа (abelian group). Если группа (S, ) удовлетворяет условию |S| < , т.е. количество ее элементов конечно, то она называется конечной (finite group).

Если (S, ) — группа, S' S и (S', ) — тоже группа, то (S', ) называется

подгруппой (subgroup) группы (S, ). Например, четные числа образуют подгруппу группы целых чисел с операцией сложения. Полезным инструментом для распознавания подгрупп является сформулированная ниже теорема.

Теорема. (Непустое замкнутое подмножество конечной группы является подгруппой).

Если (S, ) — конечная группа, a S' - любое непустое подмножество множества S, такое что

a b S' для всех a,b S', то S', ) — подгруппа группы (S, ).

Условие Целые числа a и b таковы, что 56a = 65b. Докажите, что a + b - составное число. Подсказка Выразите a + b через a. Решение 65(a + b) = 65a + 65b = 65a + 56a = 121a. Так как числа 65 и 121 взаимно просты, то a + b делится на 121. Поскольку 121 - составное число, то и a + b - составное.

13

На основе определения операции сложения по модулю n определяется аддитивная группа по модулю n (additive group modulo n) (). Размер аддитивной группы по модулю n равен

На основе операции умножения по модулю n определяется мультипликативная группа по модулю n (multiplicative group modulo n) (). Элементы этой группы образуют множество , образованное из элементов множества , взаимно простых с n:

Чтобы убедиться, что группа вполне определена, заметим, что для 0 <= а < n при всех целых к выполняется соотношение а = (а + кn) (modn). Поэтому из НОД (a, n) = 1, для всех целых к следует,

что НОД (a + nk, n) = 1. Поскольку = {а + kn : k Z}, множество вполне определено. Примером такой группы является множество

= {1,2,4,7,8,11,13,14}, в качестве групповой операции в которой выступает операция умножения по модулю 15.

gcd((2^100-1) ,(2^120-1) ) Since ,a^nb^n=(ab)K =>(2^100-1)=(2^20-1)k and 2^120-1= (2^20-1)m where gcd(k,m)=1 hence, gcd((2^100-1) ,(2^120-1) ) = (2^20-1)

gcd=НОД (Наибольший общий делитель)

Например, можно найти НОД чисел 2120 -1 и 2100 -1. Это будет равно 220 -1 – последний ненулевой остаток = наибольший общий делитель. Или НОД чисел 111…1 – сто единиц и 111…1 – шестьдесят единиц. НОД = 111…1 – двадцать единиц. Зная НОД, естественно, сразу, не разлагая на множители, находим НОК (наименьшее общее кратное) чисел a, b .

14

Необходимость Пусть p - простое. Способ 1. Рассмотрим . Множество ненулевых классов классов вычетов по простому модулю p по умножению является группой, и тогда - это произведение всех элементов группы . Поскольку - группа, то для каждого ее элемента существует единственный обратный элемент . Соответствие разбивает группу на классы: если (что равносильно , то есть , поскольку у уравнения второй степени может быть не более двух решений), то класс содержит один элемент , в противном случае класс состоит из двух элементов - . Значит, если класс содержит один элемент , то произведение всех его элементов равно , а если класс содержит 2 элемента, то произведение всех его элементов равно 1. Теперь в произведении сгруппируем элементы по классам, все произведения по 2-хэлементным классам просто равны 1: ■ Способ 2. Группа циклична, т.е. существует элемент такой, что для всякого элемента существует такое, что . Поскольку имеет элемент, то пробегает значения от 0 до , когда пробегает всю группу вычетов. Тогда ■ Способ 3. - поле, поэтому в нем имеет место теорема Безу, т.е. многочлен степени имеет не более корней. Рассмотрим многочлены и . Оба многочлена имеют корни (для это получается по малой теореме Ферма), степени многочленов равны , старшие коэффициенты одинаковы. Тогда многочлен имеет как минимум те же корней, но его степень не более . Значит по теореме Безу тождественно равен нулю, т.е. для всех будет , в частности , что равносильно . Получаем утверждение теоремы для , т.к. четно и значит .■ Достаточность Если составное и , то , а при получаем .

15

16

Теорема (Теорема Эйлера).

При любом целом значении n > 1 для всех a

Теорема (Теорема Ферма).

Если р — простое число, то для всех a

Доказательство.

Согласно уравнению Ф(р) = р – 1, для простых чисел р функция Эйлера равна ф (р) = р — 1.

Это следствие применимо к каждому элементу группы за исключением нуля, поскольку Однако для всех а , если р — простое число, справедливо соотношение .

Если , то каждый элемент группы является степенью элемента g по модулю n, и говорят, что g — первообразный корень (primitive root), или генератор (generator) группы . Например, 3 — первообразный корень по модулю 7, но 2 таковым не является. Если в группе существует первообразный корень, то говорят, что она циклическая (cyclic).

17

18

19

19. Условие Найдите остатки от деления а) 1989 × 1990 × 1991 + 19922 на 7; б) 9100на 8. Решение Произведение (сумма) двух целых чисел дает такой же остаток при делении на n, как и произведение (сумма) их остатков при делении на n. а) Данное выражение дает при делении на 7 такой же остаток, как и 2 × 3 × 4 + 52 = 49. Значит, искомый остаток равен 0. б) Данное выражение дает при делении на 8 такой же остаток, как и 1100 = 1. Ответ а) 0; б) 1.

20

20. 143=11*13. Значит если число делится и на 11 и на 13 то оно делится и на 143, так как 11 и 13 простые. Нам нужно доказать что Но если мы докажем что и , то мы докажем что 7^120-1 делится на 143. Используем малую теорему ферма и получим что: . Возведем обе части в натуральную степень 12 получим что . То есть . Таким же образом доказывается для числа 13.

21 Теорема 31.17. Для любой конечной группы E, ф) и любого ее элемента a € S

порядок элемента равен размеру генерируемой им подгруппы, т.е. ord (a) = |(a)|.

Следствие 31.18. Последовательность аA\с№\ ... является периодической с пе-

риодом t = ord (а); т.е. a^ = a^') тогда и только тогда, когда г = j (modi).

Теорема 31.20. Для всех положительных целых чисел а и п из соотношения

d = gcd (a, n) следует, что

(а) = (d) = {0, d, 2d,..., {{n/d) - 1) d} C1.22)

в Zn, так что I (a) I = n/d.

22

23

24

25

Дихотомический алгоритм возведения в степень.

В общем виде дихотомический алгоритм позволяет вычислить n–ю степень в

моноиде. Будучи применён к множеству целых чисел с операцией сложения, этот

метод позволяет умножать два целых числа и более известен как египетское

умножение.

Классический алгоритм возведения в степень посредством последовательного

умножения характерен, главным образом, своей неэффективностью в обычных

обстоятельствах – его время работы линейным образом зависит от показателя

степени.