
- •Контрольная работа 6 Обыкновенные дифференциальные уравнения
- •Основные теоретические сведения
- •1. Основные понятия теории дифференциальных уравнений 1-го порядка
- •Геометрический смысл основных понятий
- •Что есть что?
- •Чтобы решить однородное уравнение, нужно
- •Что необходимо для решения линейных уравнений
- •Что необходимо для решения уравнений 2-го порядка допускающих понижение порядка
- •Что нужно знать для составления общих решений уравнения
- •Контрольная работа 7 Теория рядов
- •Основные теоретические сведения
- •Для определения области сходимости степенного ряда
- •Контрольная работа 8 Дифференциальное исчисление функций нескольких переменных
- •Основные теоретические сведения
- •Чтобы изменить порядок интегрирования
Чтобы изменить порядок интегрирования
в данном повторном интеграле, нужно:
1) записать область интегрирования по пределам повторного интеграла в виде неравенств и построить их;
2) записать область интегрирования иначе, изменив порядок интегрирования на обратный порядок интегрирования;
3) расставить новые пределы.
В результате перемены порядка интегрирования может вместо одного интеграла получиться два и больше и, наоборот, из нескольких – один повторный интеграл.
Помните, что внешние пределы постоянны, а внутренние чаще всего переменны.
▲ 1)
Из пределов интегрирования в повторном
интеграле следует, что область
интегрирования G
данного повторного интеграла ограничена
прямыми линиями
![]() и
и
![]() ,
линией
,
линией
![]() и прямой
и прямой
![]() ,
т. е.
,
т. е.
![]()
Линия
![]() представляет собой дугу окружности
представляет собой дугу окружности
![]() с центром в точке
с центром в точке
![]() и радиусом равным 1 (см. рис. 8).
и радиусом равным 1 (см. рис. 8).
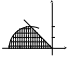 у
у
![]()
![]()
−0.5
−2 −1 O х
Рис. 8
2)
Область интегрирования G,
правильная относительно оси Oy,
проектируется на ось Ox
в отрезок
![]() .
Верхняя граница области интегрирования
.
Верхняя граница области интегрирования
![]() на отрезке
задана двумя аналитическими выражениями:
на отрезке
задана двумя аналитическими выражениями:
![]() и
и
![]() .
Следовательно, разбиваем область
интегрирования прямой, параллельной
оси Oy и проходящей
через точку пересечения линий
и
,
абсцисса которой ,
на две области
.
Следовательно, разбиваем область
интегрирования прямой, параллельной
оси Oy и проходящей
через точку пересечения линий
и
,
абсцисса которой ,
на две области
![]() и
и
![]() :
:
![]()
3)
Получаем
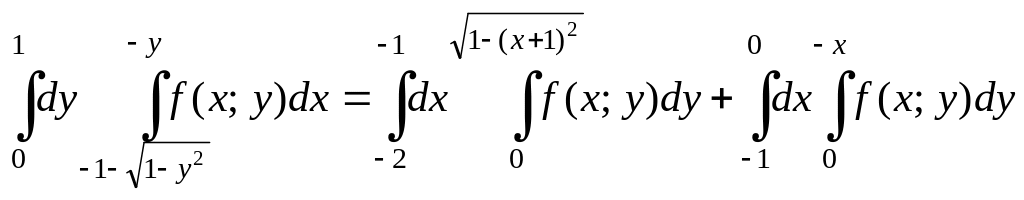 .
▼
.
▼
Пример
2. Вычислить объем тела, ограниченного
поверхностями
![]() ,
,
![]() .
.
▲ По
заданным уравнениям поверхностей строим
область методом
сечений (находим сечения тела координатными
плоскостями и плоскостями, параллельными
им):
![]() парабола;
парабола;
![]() парабола;
парабола;
![]() окружность.
окружность.
Следовательно,
![]() параболоид вращения.
Область G (сечение
параболоида плоскостью
параболоид вращения.
Область G (сечение
параболоида плоскостью
![]() )
окружность
)
окружность
![]() .
.
Перейдем к цилиндрической системе координат.
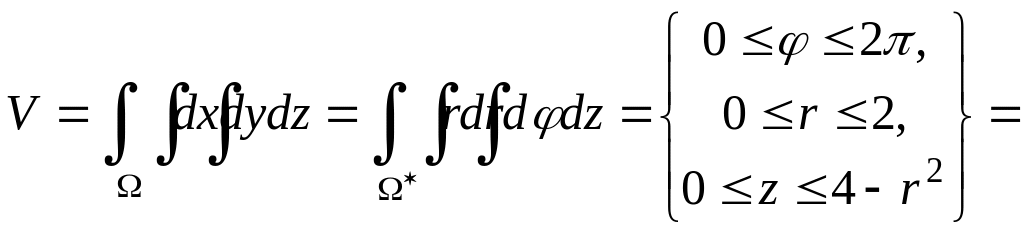
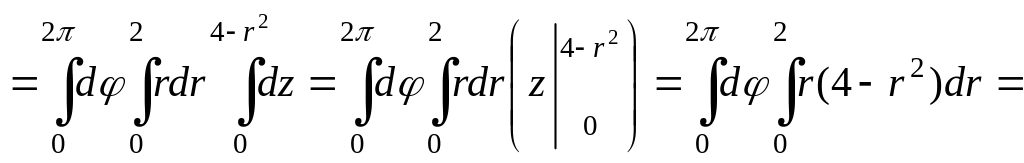
![]() .
▼
.
▼
Пример
3. Вычислить криволинейный интеграл
![]() от точки
от точки
![]() до точки
до точки
![]() :
1) по прямой линии
:
1) по прямой линии
![]() ,
2) по дуге параболы
,
2) по дуге параболы
![]() ,
3) по дуге эллипса
,
3) по дуге эллипса
![]() .
.
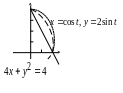 у
у
1
O 0.5 х
![]()
Рис. 9
▲ Сделаем чертеж (рис. 9).
1)
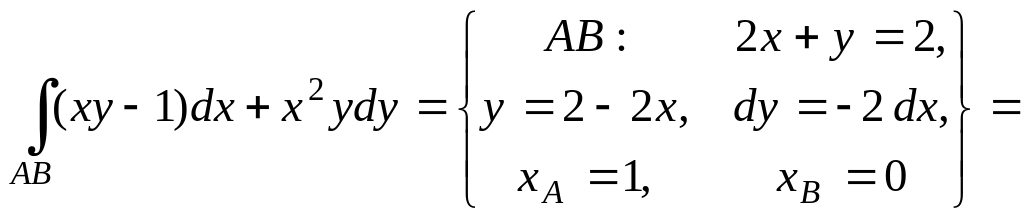
![]()
![]() .
.
2)
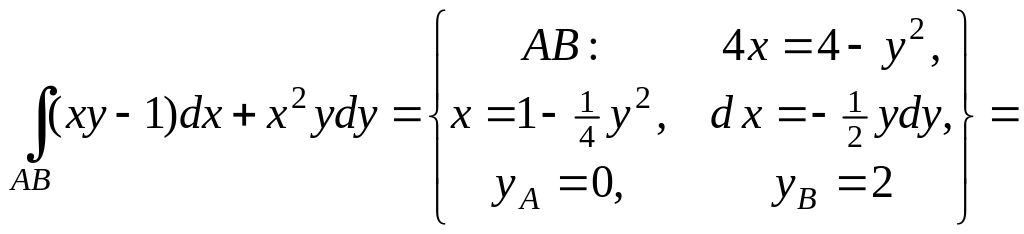
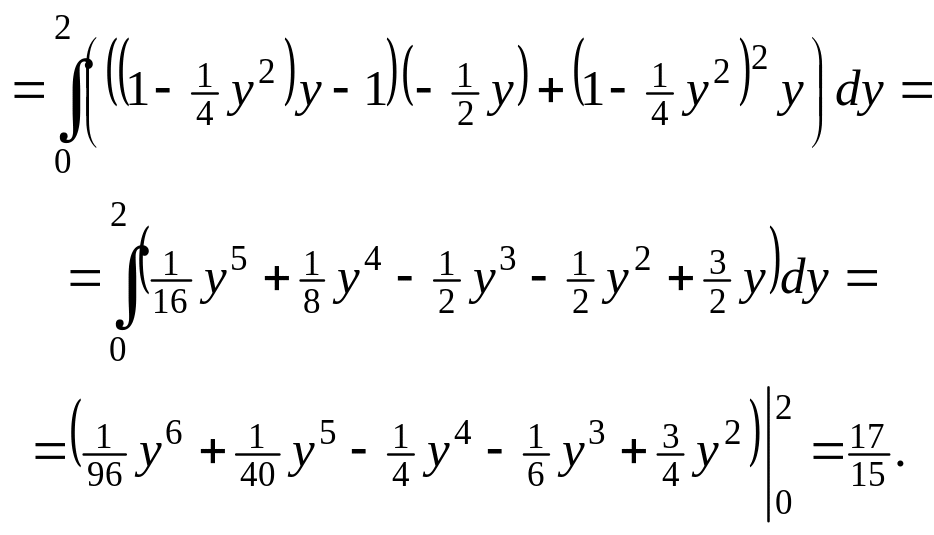
3)
![]()
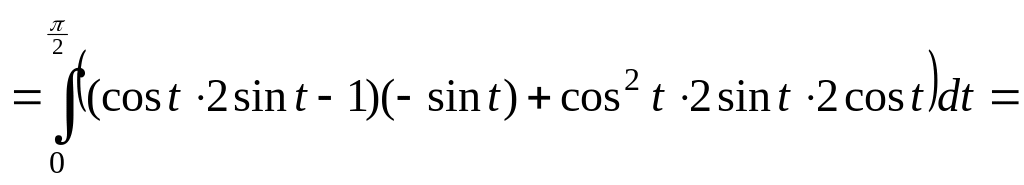
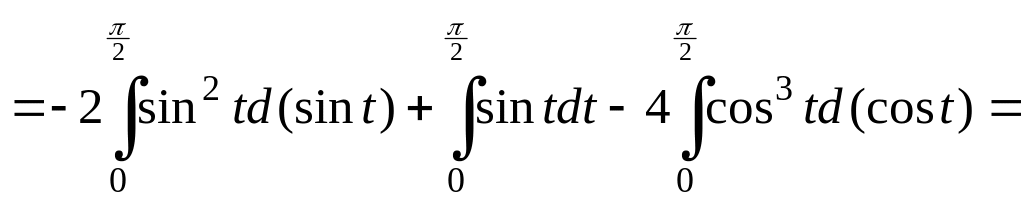
![]() .
▼
.
▼
Пример
4. Вычислить поток векторного поля
![]() через замкнутую поверхность S,
образованную плоскостью
через замкнутую поверхность S,
образованную плоскостью
![]() и частью конуса
и частью конуса
![]() .
Проверить результат с помощью формулы
ОстроградскогоГаусса.
.
Проверить результат с помощью формулы
ОстроградскогоГаусса.
▲ Поверхность
S состоит из двух
поверхностей:
![]() части конуса
части конуса
![]() и
и
![]() части плоскости
.
Поэтому поток через поверхность S
равен сумме потоков вектора a
через составляющие поверхности:
части плоскости
.
Поэтому поток через поверхность S
равен сумме потоков вектора a
через составляющие поверхности:
![]() ,
,
где
![]() и
и
![]() внешние единичные
нормали к конусу и плоскости соответственно
(см. рис. 10).
внешние единичные
нормали к конусу и плоскости соответственно
(см. рис. 10).
 у
у
 n2
n2

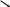 n1
n1
 О х
О х
Рис. 10.
Вычислим
поток через поверхность
,
уравнение которой в явном виде
![]() (так как
(так как
![]() ).
Исключая z из уравнений
и
).
Исключая z из уравнений
и
![]() ,
получим уравнение границы области G
(проекции поверхности
на плоскость
,
получим уравнение границы области G
(проекции поверхности
на плоскость
![]() ):
):
![]() .
Вектор внешней нормали к поверхности
.
Вектор внешней нормали к поверхности
![]()
![]()
![]() .
.
Здесь
в выражении для нормали выбран знак
«», так как угол
между осью
![]()
и
нормалью n1
тупой, и, следовательно,
![]() .
.
Найдем
скалярное произведение векторов
![]()
![]() .
.
Учитывая, что на поверхности
![]() ,
,
по
формуле (9.16) получаем
![]() .
Область G есть круг
.
Область G есть круг
![]() .
Поэтому переходим к полярным координатам
.
Поэтому переходим к полярным координатам
![]()

![]()
![]()
![]()
Вектор
внешней нормали к поверхности
![]()
![]() .
.
Здесь
в выражении для нормали выбран знак
«+», так как
![]() .
Тогда имеем
.
Тогда имеем
![]() ;
;
![]() ;
;
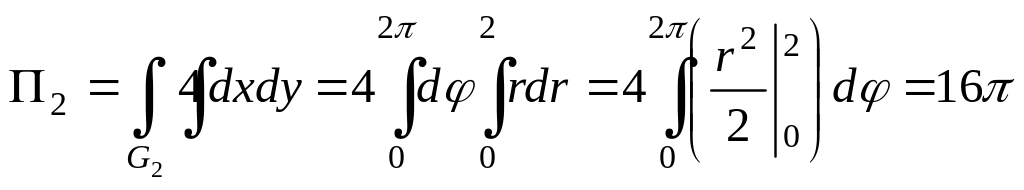 .
.
Таким
образом, поток векторного поля через
поверхность
![]() равен
равен
![]() .
.
Найдем
решение этой задачи с помощью формулы
ОстроградскогоГаусса
(9.20). Дивергенция поля
![]() равна
равна
![]() ,
,
а поток (в цилиндрической системе координат)
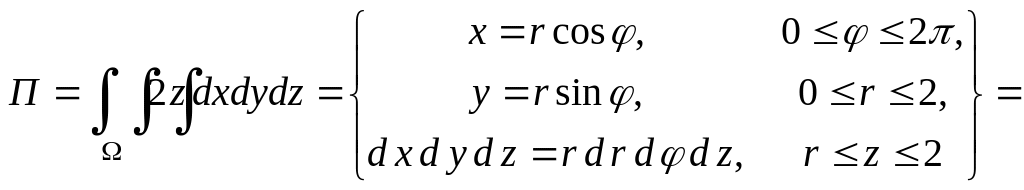
![]()
![]() .
.
Следовательно,
как и в первом случае,
![]() .
▼
.
▼
Пример
5. Вычислить циркуляцию векторного
поля
по контуру l, образованному
пересечением поверхностей
![]()
![]() и
и
![]() .
Проверить результат
с помощью формулы Стокса.
.
Проверить результат
с помощью формулы Стокса.
▲ Пересечением
указанных поверхностей (см. пример 4)
является окружность
.
Направление обхода контура выбираем
так, чтобы ограниченная им область G
(круг) оставалась слева. Запишем
параметрические уравнения контура
(окружности)
![]() .
По формулам (9.20) и (9.15) получаем
.
По формулам (9.20) и (9.15) получаем

![]()
![]()
![]() .
.
Применим
теперь формулу Стокса (9.21). При возрастании
параметра t от 0 до 2
движение по окружности происходит
против часовой стрелки относительно
единичного вектора
![]() .
Ротор данного векторного поля находим
по формуле (9.18)
.
Ротор данного векторного поля находим
по формуле (9.18)

![]()
![]() .
.
Скалярное
произведение вектора
на вектор
![]()
![]() .
.
Поэтому искомая циркуляция (9.21)
![]()
![]()
![]() ,
,
что совпадает со значением циркуляции, полученным непосредственным вычислением.
Вопросы для самопроверки
1. Что такое интегральная сумма?
2. Что называется двойным интегралом от функции по области X? Укажите его геометрический смысл.
3. Сформулируйте теоремы о двойном интеграле от суммы и вынесении постоянного множителя за знак двойного интеграла.
4. Напишите формулы, выражающие линейность и аддитивность двойных интегралов.
5. Сформулируйте теорему о формуле среднего значения для двойного интеграла, аналогичную теореме для определенного интеграла.
6. Что называется повторным интегралом от функции по области X? Как он вычисляется?
7.
Сведите двойной интеграл
![]() к повторному интегралу двумя способами,
если G − круг, ограниченный окружностью
к повторному интегралу двумя способами,
если G − круг, ограниченный окружностью
![]() .
.
8.
Что называется тройным интегралом от
функции
по пространственной области
![]() ?
?
9. Что называется трехкратным интегралом от функции по области V? Как он вычисляется?
10. Напишите формулы, выражающие линейность и аддитивность тройных интегралов.
11. Сформулируйте теорему о среднем для тройного интеграла.
12. Сформулируйте определения: а) интегральных сумм для криволинейного интеграла 1-го рода; б) предела интегральных сумм.
13. Что называется криволинейным интегралом по координатам? Сформулируйте известные вам свойства криволинейного интеграла.
14. Сформулируйте определения: а) интегральных сумм для криволинейного интеграла 2-го рода; б) предела интегральных сумм.
15. Что называется криволинейным интегралом по длине дуги плоской кривой?
16.
Как вычисляется криволинейный интеграл
по кривой, заданной уравнением
![]() ?
?
17. Какое направление обхода замкнутой кривой принимают за положительное направление?
18.
Каков смысл обозначения
![]() ?
?
19. Сформулируйте теорему о связи между криволинейными интегралами 1-го и 2-го рода.
20. Сформулируйте свойства линейности и аддитивности криволинейных интегралов 2-го рода.
21. Напишите формулу Грина и сформулируйте условия, при которых она верна.
22. Выведите формулу для вычисления площади плоской фигуры с помощью криволинейного интеграла.
23. Что означает утверждение: «Криволинейный интеграл не зависит от пути интегрирования»?
24.
Что означает утверждение: «Выражение
![]() является полным дифференциалом в области
G?
является полным дифференциалом в области
G?
25. Дайте определение односвязной области на плоскости.
26. Что называется поверхностным интегралом? Напишите формулы для его вычисления.
27. Сформулируйте понятие векторного поля.
28. Дайте определение поверхности: а) двусторонней; б) односторонней; в) ориентированной.
29. Каким характеристическим свойством обладает, двустороння поверхность; односторонняя поверхность?
30. Зависят ли от ориентации поверхности: а) поверхностный интеграл 1-го рода и его интегральные суммы; б) поверхностный интеграл 2-го рода?
31. Как вводится положительное направление обхода контура, согласованное с ориентацией поверхности, ограниченной этим контуром?
32. Напишите формулу Стокса и сформулируйте условия, при которых эта формула верна.
33. Напишите формулу Остроградского-Гаусса и сформулируйте условия, при которых эта формула справедлива.
34. Дайте определение скалярного и векторного полей и приведите примеры физических полей.
35. Что такое поверхности уровня?
36. Что такое векторные линии?
37. Дайте определение производной по направлению для скалярного и векторного полей. Как связана производная по направлению с частными производными?
38.
Найдите производную скалярного поля
![]() в точке
в точке
![]() по направлению: а) оси Ox;
б) оси Oy; в) вектора l
= {1; 1; 1}.
по направлению: а) оси Ox;
б) оси Oy; в) вектора l
= {1; 1; 1}.
39. Дайте определение градиента скалярного поля. Как связана производная по направлению l с градиентом скалярного поля в данной точке?
40. Какое векторное поле называется потенциальным?
41. Дайте определение дивергенции векторного поля. Каков физический смысл дивергенции?
42. Что называется потоком векторного поля?
43. Дайте определение ротора векторного поля. Каков физический смысл ротора?
44. Какое векторное поле называется безвихревым?
45. Какое векторное поле называется соленоидальным?
46. Что такое оператор Гамильтона?
47. Запишите с помощью оператора Гамильтона: а) градиент скалярного поля; б) дивергенцию векторного поля; в) ротор векторного поля; г) формулу для производной скалярного поля по направлению l.
48.
Используя правила вычислений с оператором
Гамильтона, докажите, что
![]() .
.
49. Что такое полная производная; локальная производная? Что они характеризуют и каким соотношением связаны?
После изучения тем ”Общая схема построения интегралов. Теория поля“ выполните контрольную работу 9.
