10. Теорема о разложении определителя по произвольному столбцу
Один из методов вычисления определителей высших порядков - разложение их по строке/столбцу.
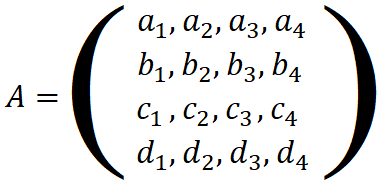
Это следствие позволяет разложить определитель по элементам некоторой строки или столбца: то есть зафиксировав строку/столбец, умножить каждый элемент на его алгебраическое дополнение и сложить с остальными элементами, над которыми было проделано то же самое действие.
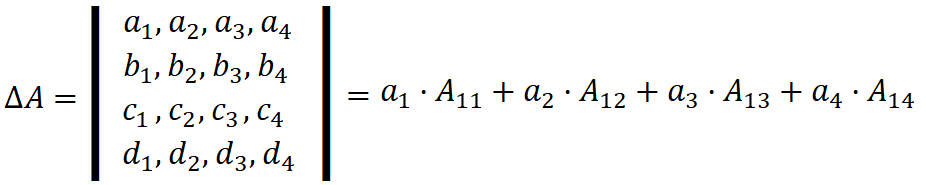
При этом вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка - в данном примере вместо нахождения одного определителя четвертого порядка, мы находим четыре определителя третьего порядка.
Данный метод является частным случаем теоремы Лапласа, где один из аргументов суммы равен единице: то есть при фиксации одной строки или столбца, а не всех элементов матрицы одновременно.
Теорема Лапласа:
Именно поэтому такое преобразование именуют понижением порядка определителя.
11. Теорема Крамера
Теорема Крамера: система уравнений квадратного вида имеет решение тогда и только тогда, когда ее определитель отличен от нуля.
Иначе: в заданной системе n линейных уравнений от n неизвестных, решением будет являться
Где Δ - определитель матрицы из коэффициентов перед неизвестными, а Δi - определитель матрицы, в которой i-ый столбец заменен на столбец со свободными членами - правыми частями неравенств.
Применяется только если Δ ≠ 0.
При попытках выразить значение xn переменной, мы придем к правилу Крамера:
Пример указан для матрицы 3х3.
Которое будет невозможно вычислить, если знаменатель будет равен нулю. Также, если знаменатель не будет равен нулю, то из-за того, что коэффициенты перед неизвестными всегда будут одними и теми же, то и решение для системы уравнений будет единственным.
12. Теорема об определителе с углом нулей
Пусть дана матрица M, состоящая из четырех других матриц - A, B, C и D соответственно:
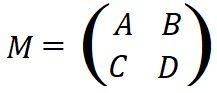
Тогда если один из углов B или C равен нулю, то:
А если A или D равен нулю, то:
Доказательство: на примере, где все элементы матрицы C являются нулями. Приведем матрицу M к треугольному виду элементарными преобразованиями:
Преобразуем первые kA строк (до А), чтобы матрица А приобрела треугольный вид ;
Затем преобразуем kD, начиная с конца (до D), чтобы матрица D приобрела треугольный вид.
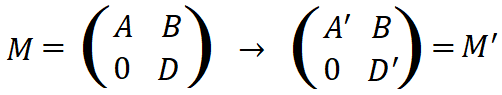
Где штрихи символизируют изменение. Теперь, при нахождении определителя матрицы M’ мы можем разложить ее по первому столбцу:
Что эквивалентно:
Но так как мы применяли элементарные преобразования для преобразования A и D, то определители изменившихся матриц равны определителям изначальных матриц:
Доказательства для других углов аналогичны.
13. Сложение матриц и умножение их на число
Сложение матриц А и В – это нахождение такой матрицы С, все элементы которой представляют собой сложенные попарно соответствующие элементы исходных матриц А и В. Складывать допускается только матрицы одинаковой размерности (допустим m × n), т.е. имеющие равное количество строк и равное количество столбцов.
Свойства сложения матриц:
Коммутативность: A + В = В + А
Ассоциативность: А + (В + С) = (А + В) + С
Сложение с нулевой матрицей: А + О = А Нулевая матрица O – матрица, все элементы которой имеют нулевое значение.
Существование противоположной матрицы: А + (-А) = О
Умножение матрицы на число:
Для того, чтобы произвести умножение матрицы A на произвольное число α, нужно все элементы матрицы A умножить на число α.
Свойства умножения на число:
Дистрибутивный закон относительно матриц: λ⋅(A+B)=λA+λB
Дистрибутивный закон относительно действительных (комплексных) чисел: (λ+μ)⋅A=λA+μA
Ассоциативный закон: λ⋅(μ⋅A)=(λ⋅μ)
Есть особое число λ=1, благодаря которому матрица остаётся неизменной 1⋅A=A⋅1=A
Умножение матрицы на ноль приводит к тому, что каждый элемент матриц обнуляется и матрица становится нулевой той же размерности, которой была изначально: 0⋅A=0