
- •Глава 1:введение в анализ.
- •–Область определения функции. –область значения функции.
- •Параграф 3: последовательность.
- •Параграф 4: предел последовательности.
- •Параграф 5. Предел действительной функции одного действительного переменного
- •Параграф 6: бесконечно малые величины.
- •Параграф 9: теоремы о пределах.
- •Параграф 10: одностороние пределы слева и справа точки .
- •Параграф 11: предел функции на бесконечности.
- •Параграф 12: замечательные пределы.
- •Параграф 13: сравнение бесконечно маЛых.
- •Параграф 14. Классификация точек разрыва
МАТЕМАТИЧЕСКИЙ АНАЛИЗ.
Глава 1:введение в анализ.
ПАРАГРАФ 1:МНОЖЕСТВА.
Понятие множества – первичное понятие, не определяемое через более простые.
Слова: совокупность, семейство, набор – его синонимы.
Примеры множеств: множество студентов в аудитории, множество преподавателей на кафедре, множество автомобилей на стоянке и пр.
Первичными понятиями также являются понятия элемента множества и отношения между элементами множества.
Условимся обозначать множества заглавными буквами: A, B, C, X, Y, …, а их элементы – строчными: a, b, c, x, y, …
Опр1. Множество называется конечным, если оно состоит из определённого конечного числа элементов. В противном случае оно называется бесконечным.
Например, множество студентов в аудитории конечно, а множество натуральных чисел или множество точек внутри отрезка бесконечно.
Опр2. Множество, не содержащее ни одного элемента, называется пустым.
Опр3. Два множества называются равными, если они состоят из одних и тех же элементов.
Пример. А={1, 3, 5}, B={5, 1, 3} A=B.
Т.е. понятие множества не подразумевает того или иного порядка следования элементов.
Опр4. Множество Х называется подмножеством множества Y, если любой элемент множества Х является элементом множества Y (при этом, вообще говоря, не любой элемент множества Y является элементом множества X).
Например, множество апельсинов O является подмножеством множества фруктов F , а множество натуральных чисел N является подмножеством множества вещественных чисел R.
Считают, что каждое множество является подмножеством самого себя. Пустое множество является подмножеством любого множества.
Опр5. Любое непустое подмножество В множества А, не равное А, называется собственным подмножеством.
Опр. 6: Суммой множеств (объединением) – называют множество, каждый элемент которого принадлежит хотя бы одному из данных множеств.
![]()
![]()
![]() –объединение
множеств.
–объединение
множеств.

Общий элемент указывается один раз.
Опр. 7: Пересечением множеств (произведением) называется множество, каждый элемент которого принадлежит данным множествам.
![]()
![]() –пересечение.
–пересечение.

Опр.
8:
Разностью множеств
![]() и
и
![]() называют
называют
![]() множество,
каждый элемент которого принадлежит
множество,
каждый элемент которого принадлежит
![]() и не принадлежит
и не принадлежит
![]() .
.

Промежутки.
Вся ось![]() – множество вещественных чисел.
– множество вещественных чисел.

![]()
![]() –замкнутый
промежуток – сегмент.
–замкнутый
промежуток – сегмент.
![]()
![]() –открытый
промежуток (интервал).
–открытый
промежуток (интервал).
![]()
![]() –полузамкнутый.
–полузамкнутый.
![]()
РАЗЛИЧНЫЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ.
1. Первичное множество
N = {1, 2, 3….} – (применяются для счета предметов) множество натуральных чисел.
2. {0, 1, 2, 3, 4…} – множество целых неотрицательных чисел.
3. Z = {0, ±1, ±2…} – множество целых чисел.
4. Q = {p/q} – рациональное множество чисел, где P Î Z, q = N.
Во множестве Q возможны все 4 арифметических действия, за исключением деления на нуль.
Множество иррациональных чисел – множество чисел, которые изображаются бесконечными не периодичными десятичными дробями.
Множество вещественных чисел (действительных) – множество, являющееся объединением Q и иррациональных чисел.
R – множество вещественных чисел.
R = Q È {иррациональные числа}.
Свойства вещественных чисел:
Упорядоченность.
Для любых двух вещественных чисел верно одно и только одно соотношение:

Плотность:
Между двумя любыми не равными вещественными числами лежит бесконечное множество других вещественных чисел.
Неограниченность:
Каким
бы не было вещественное число
![]() ,
всегда существует точка
,
всегда существует точка
![]() ,
что
,
что
![]() ,
и всегда
существует
,
и всегда
существует
![]() ,
что
,
что
![]() .
.
Несчетность.
Вещественные
числа нельзя занумеровать, т. к. их больше
натуральных (![]() поддается нумерации.)
поддается нумерации.)
Непрерывность.
Опр.
9:
Множество
![]() называется ограниченным с верху, если
существует его верхняя граница
называется ограниченным с верху, если
существует его верхняя граница
![]() (число, которое
не меньше всех чисел множества А)
(число, которое
не меньше всех чисел множества А)

Если существует верхняя граница хоть одна, то существует бесчисленное множество верхних границ.
Опр. 10:
Наименьшей из верхних границ, ограничивающих
с верху числовое множество
![]() ,
называется его точной верхней границей.
,
называется его точной верхней границей.
Обозначается:
![]() (supremum)
(supremum)
Опр. 11:
Множество
![]() называется ограниченным снизу, если
существует его нижняя граница в
(число, которое не больше всех чисел
множества
называется ограниченным снизу, если
существует его нижняя граница в
(число, которое не больше всех чисел
множества
![]() ).
).

Если существует хотя бы одна нижняя граница, то существует бесчисленное множество нижних границ.
Опр. 12:
Наибольшая из нижних границ, ограниченного
снизу числового множества
![]() ,
называют точной нижней границей.
,
называют точной нижней границей.
Обозначается:
![]() (infimum).
(infimum).
Опр. 13: Множество называется ограниченным, если оно ограничено и сверху и снизу.
Формулировка свойства непрерывности множества вещественных чисел.
Если числовое множество
 ограниченно сверху, то оно имеет точную
верхнюю границу.
ограниченно сверху, то оно имеет точную
верхнюю границу.Если числовое множество
 ограниченно
снизу, то оно имеет точную нижнюю
границу.
ограниченно
снизу, то оно имеет точную нижнюю
границу.
Важнейшую роль в математическом анализе играет понятие окрестности точки числовой оси.
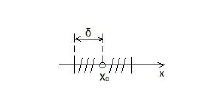
Опр 14. δ -окрестностью точки x0 называют интервал длиной 2δ с центром в точке x0

Опр15. Проколотой δ -окрестностью точки называется окрестность этой точки, из которой исключена сама точка x0
ПАРАГРАФ 2: ФУНКЦИЯ
Опр.
1:
Переменная величина
![]() называется функцией аргумента
называется функцией аргумента
![]() ,
если каждому рассматриваему значению
,
если каждому рассматриваему значению
![]() из некоторого множества
из некоторого множества
![]() соответствует единственное значение
соответствует единственное значение
![]() из множества
из множества
![]() .
.
