Лекции по дискретной математикеl

Если выполнено только свойство 2, множество f называют частичной функцией.

Функция f : X ! Y называется

сюръективной, если она обладает свойством

10: (8y 2 Y )(9x 2 X)(x; y) 2 f (у каждого элемента y из множества Y есть хотя бы один "прообраз"),

инъективной, если она обладает свойством

20: (8y 2 Y )(8x1; x2 2 X)(x1; y) 2 f ^ (x2; y) 2 f ! x1 = x2 (у каждого элемента y

из множества Y не более одного "прообраза"),

биективной (или взаимно-однозначной ), если она одновременно инъективна и сюръекетивна.

На рисунках выше последовательно изображены сюръективная, но не инъективная; инъективная, но не сюръективная; взаимно-однозначная функции и функция, которая не является ни инъективной, ни сюръективной. Условие инъективности функции f : X ! Y можно еще переписать так:

(8x1; x2 2 X)f(x1) = f(x2) ! x1 = x2:

Пример. Функция f : R ! R, заданная формулой f(x) = x2 не сюръективна, поскольку число 1 не имеет прообраза, и не инъективна, поскольку число 1 имеет сразу два прообраза 1 и 1: 1 = 12 = ( 1)2. Если рассмотреть ограничение этой

функции на множество R 0 = fx 2 R: x 0g всех неотрицательных действительных чисел (т.е. функцию f : R 0 ! R 0, заданную той же формулой), она становится взаимно-однозначной. Функция g : R ! R, заданная формулой g(x) = x3 взаимно-

однозначна на всей области определения (для строго доказательства двух последних фактов требуются сведения из математического анализа ).

11

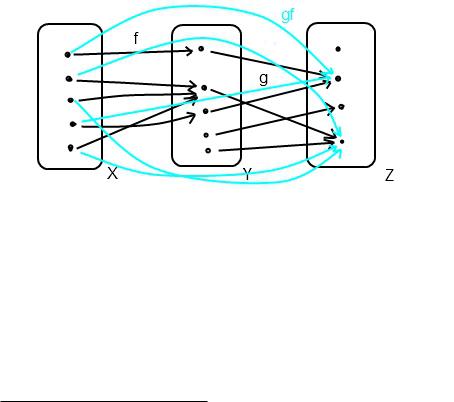
Если для функции f : X ! Y множество f(y; x): (x; y) 2 fg также является функ-

цией, то это множество называется обратной функцией для функции f и обозначается символом f 1. Функция f называется обратимой, если существует функция f 1. Несложно доказать следующее

Предложение 1. Каждая функция обратима тогда и только тогда, когда она взаимно-однозначна.

Тождественной функцией на множестве X называется функция eX, которая каж- дому элементу x множества X ставит в соответствие сам элемент x:

eX = f(x; x): x 2 Xg:

Если даны две функции f : X ! Y и g : Y ! Z, то определена композиция этих функций, обозначаемая символом g(f) или просто gf, т.е. множество

f(x; z): (9y 2 Y )(f(x) = y) ^ (g(y) = z)g:

Свойства композиции функций сформулируем в виде следующих предложений.

Предложение 2. Композиция сюръективных функций сюръективна . Композиция инъективных функций инъективна.

Предложение 3. Пусть даны функции f : X1 ! X2, g : X2 ! X3 è h: X3 ! X4. Тогда h(gf) = (hg)f.5

Предложение 4. Пусть даны функции f : X ! Y и g : Y ! X. Тогда функция g есть обратная для функции f тогда и только тогда, когда gf = eX è fg = eY .

Мощностью конечного множества называется число его элементов. Мощность множества X обозначается символом jXj.6

Имеет место следующее

5Поэтому при записи "длинных" композиций скобки опускают.

6Множество X называется конечным, если для некоторого натурального числа n 2 ! существует взаимно-однозначное отображение f : n ! X. Можно доказать, что для каждого конечного множества X такое число n единственно. Оно называется числом элементов или мощностью X.

12

Предложение 5. Пусть даны конечные множества X и Y . Тогда

öèÿ f : Y ! X.

2: jXj = jY j тогда и только тогда, когда существует взаимно-однозначная функция f : X ! Y .

Понятие мощности множества распространяется и на бесконечные множества. Для его строгого определения требуются дополнительные теоретико-множественные конструкции, которые мы обсуждать не будем. Важным является то, что на мощностях множеств можно ввести линейный порядок с сохранением свойств из предложения 5. Т.е. "сравнивать" множества по мощности можно и не имея точного определе-

ния мощности. При этом очень полезной оказывается следующая

Теорема 1. Для любых множеств X и Y если существуют инъективные функции f : X ! Y и g : Y ! X, то множества X и Y равномощны (т.е. существует биективная функция h: X ! Y ).

Доказательство этой теоремы, несложное, но требующее изобретательности, можно найти в [3].

Множества, которые равномощны множеству натуральных чисел !, называются счетными. Иными словами, каждому элементу x счетного множества X можно приписать какой-нибудь натуральный номер n (задействовав все натуральные числа в ка-

честве номеров) и выстроить множество X в последовательность x0; x1; x2; : : : ; xn; : : :.

Например, счетными являются множества всех четных чисел, всех степеней двоек, всех простых чисел и т.п. Вообще, можно показать, что каждое подмножество счетного множества (в частности, множества натуральных чисел !) либо конечно,

либо счетно.

Покажем далее, что множество всех пар натуральных чисел счетно. Положим первым номером последовательности пару (0; 0). Затем в порядке возрастания первого

номера перечислим все пары (x; y) с суммой членов, равной единице, т.е. продолжим последовательность членами (0; 1) и (1; 0). Затем также поступим с парами, сумма членов которых равна 2 и т.д. Получим последовательность

(0; 0); (0; 1); (1; 0); (0; 2); (1; 1); (2; 0); : : : ;

в которую попадут все элементы множества ! !.

Аналогично можно показать счетность множества всех троек, четверок и т.п. на-

туральных чисел. Более того, можно показать, что множество всех конечных последовательностей натуральных чисел (т.е. множество !<!) тоже счетно. Один из

способов доказательства состоит в следующем. Конечно, существует инъективная функция f : ! ! !<!, которая каждому натуральному числу n ставит в соответ-

ствие последовательность (n) (длины 1). Найдем теперь инъективное отображение g : !<! ! !. Пусть p0; p1; : : : ; pn; : : : последовательность всех простых чисел. Для каждой конечной последовательности x = (x0; x1; : : : ; xn) натуральных чисел поло-

13

этой функции следует из однозначности разложения натурального числа в произведение простых.

Множества Z целых и Q рациональных чисел тоже счетны (это легко вывести из счетности множества ! ! и теоремы 1).

Можно ли привести пример несчетного множества? Да, множество всех бесконечных последовательностей натуральных чисел несчетно. Докажем это с помощью диагонального метода Кантора. Допустим, что нам удалось каким-нибудь образом перечислить все бесконечные последовательности натуральных чисел. Расположим их для наглядности в виде "таблицы"

Каждая n-ая строка этой таблицы есть последовательность с номером n, который

записан в виде верхнего индекса каждого члена последовательности. Рассмотрим диагональ этой таблицы, т.е. последовательность

x00; x11; x22; : : : xnn; : : :

и, далее, следующую последовательность

x00 + 1; x11 + 1; x22 + 1; : : : xnn + 1; : : :

По предположению последовательность присутствует в списке всех перечисленных

последовательностей и имеет свой номер n0, т.е. является n0-îé строкой изображенной

таблицы

xn0 0 ; xn1 0 ; xn2 0 ; : : : xnn0 ; : : : ;

что влечет противоречивое равенство

xn0 = xn0 + 1:

n0 n0

Аналогично можно доказать несчетность множества всех бесконечных последовательностей из нулей и единиц, откуда легко получить несчетность множества R действи-

тельных чисел.

Можно ли привести пример множества, содержащего "еще больше" элементов, чем R. Да. Некоторой модификацией диагонального метода можно доказать, что для любого множества X справедливо строгое неравенство

jXj < jP(X)j:

Таким образом, множество-степень множества R имеет мощность большую, чем jRj.

14

1.4Упражнения и задачи

1. Используя символ 2 в качестве единственного нелогического символа, записать на формальном языке следующие утверждения:

1.1.Множества X и Y имеют одни и те же подмножества.

1.2.Любая инъективная функция f : X ! X сюръективна.

1.3.Существует индуктивное множество.

S

1.4. Для любого множества X множество P(X) равно множеству X.

1.5. Ни одно непустое множество X не совпадает со своим декартовым квадратом

X X (используя определение пары (x; y) = fx; fx; ygg).

2. Проверить истинность следующих тождеств (если они истинны, доказать, если нет, привести контрпример):

2.1.X n (Y \ Z) = (X n Y ) \ (X n Z),

2.2.(X M Y ) M Z = X M (Y M Z),

2.3.X (Y [ Z) = (X Y ) [ (X Z),

2.4.P(X [ Y ) = P(X) [ P(Y ),

2.5.X Y = Y X.

3.Докажите законы двойственности x = x, x [ y = x \ y, x \ y = x [ y, используя только законы алгебры множеств 1-5, ñòð. 8.

4.Являются ли следующие функции инъективными, сюръективными, взаимнооднозначными (ответ обосновать):

4.1.функция f : f0; 1; 2; 3; 4g ! f0; 1; 2; 3; 4g, которая ставит в соответствие числу x

остаток от деления числа 5x на 4,

4.2.функция f : R ! R, заданная формулой f(x) = x + jxj (jxj означает модуль x),

4.3.функция f : R2 ! R2, которая каждой паре (x; y) 2 R2 ставит в соответствие

ïàðó (x 4y; x + 2y),

4.4.функция f : R ! R, заданная формулой f(x) = x3 4x + 1,

4.5.функция f : N ! P(P(N)), которая каждому натуральному числу n ставит в соот-

ветствие множество всех подмножеств множества N, содержащих число n в качестве

элемента.

5. Приведите пример функции f : N ! N, которая

5.1.Инъективна, но не сюръективна,

5.2.Сюръективна, но не инъективна,

5.3.Взаимно-однозначна, но не совпадает с функцией eN.

6. Пусть n натуральное число. Может ли линейный оператор A: Rn ! Rn áûòü

инъективным, но не сюръективным? Каким свойством должна обладать его матрица, чтобы он был взаимно-однозначным?

7.Приведите пример функций f и g из множества натуральных чисел в множество натуральных чисел, для которых fg 6= gf.

8.Докажите предложения 1-4 (ñòð. 12).

9.Докажите, что множество рациональных чисел счетно ( воспользоваться тем, что каждое рациональное число представляется в виде дроби ).

10.Докажите, что множество бесконечных последовательностей из нулей и единиц несчетно (надо чуть-чуть модифицировать доказательство на стр. 14 ).

15

2Отношения и их свойства. Алгебраические структуры.

3Элементы комбинаторики. Биномиальные коэффициенты. Рекуррентные последовательности.

4Замкнутые классы дискретных функций. Постовская классификация замкнутых классов булевых функций.

5 Элементы теории графов.

6 Элементы теории решеток.

Список литературы

[1]В.Б. Гисин. Дискретная математика.

[2]Э. Мендельсон. Введение в математическую логику.

[3]Н. К. Верещагин, А. Шень. Начала теории множеств. Математическая логика и теория алгоритмов.

[4]А. Френкель, И. Бар-Хилел. Основания теории множеств.

16