Лекция 2

8

Лекция 2. Экономико-математические модели оптимизационных задач.

Вопросы:

1. ЭММ задачи производственного планирования.

2. ЭММ задачи транспортных перевозок.

3. ЭММ задачи распределения производственной программы предприятия.

4. ЭММ задачи оптимизации состава промышленных смесей.

5. ЭММ задачи раскроя материалов.

1. ЭММ задачи производственного планирования.

Пусть некоторая производственная единица (цех, завод, объединение и т.д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов, может выпускать n различных видов продукции (товаров), известных под номерами, обозначаемыми индексом j ( j= 1,n ).

Ее будем обозначать П j .

При производстве этих видов продукции предприятие должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т.д.).

Все эти виды ограничивающих факторов называют ингредиентами Ri.

Пусть их число равно m;

припишем им индекс i (i =1,m ).

Они ограничены, и их количества равны соответственно

b1,... , bi,... ,bm условных единиц.

Таким образом, b = (b1;...;bi;...;bm) – вектор ресурсов.

Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т.д. Примем в качестве

такой меры, например, цену реализации

Cj ( j = 1,n ), т.е. c = (c1;...;cj;...;cn) – вектор цен.

Известны также технологические коэффициенты aij, которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-гo вида.

Матрицу коэффициентов aij называют технологической и обозначают буквой А.

Имеем A =|aij|.

Обозначим через x = (x1;...; xj;...; xn) план производства, показывающий, какие виды товаров П1;...; П j;...; Пn

нужно производить и в каких количествах, чтобы

обеспечить предприятию максимум объема реализации при имеющихся ресурсах.

Так как cj – цена реализации единицы j-й продукции, цена реализованных xj единиц будет равна cjxj , а общий объем реализации

Z=c1x1+…+cnxn

Это выражение – целевая функция, которую нужно максимизировать.

Так как aijxj — расход i-го ресурса на производство xj единиц j-й продукции, то, просуммировав расход i-го ресурса на выпуск всех п видов продукции, получим общий расход этого ресурса, который не должен превосходить

bi (i =1,m ) единиц:

ajx1..+ aijxi + …+ainxn <bi.

Чтобы искомый план x* = (x1;...; xj;...; xn) был реален, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объемы xj выпуска продукции:

xj >_ 0( j = 1,n )

Таким образом, модель задачи о наилучшем использовании ресурсов примет вид:

найти

Так как переменные xj входят в функцию Z(x) и систему ограничений только в первой степени, а показатели aij, bi, сj являются постоянными в планируемый период, то

(1) - (3) — задача линейного программирования.

2. ЭММ задачи транспортных перевозок.

Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям; при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были

полностью удовлетворены. Так как от схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача, о наиболее

рациональном прикреплении, правильном, направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.

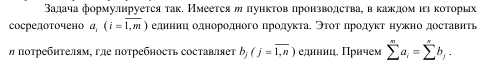
Известны величины сij – затраты на перевозку единицы продукта из i-го пункта производства в j-й пункт потребления. Обозначим через xij количество продукта, перевозимое из i-го пункта производства в j-й пункт потребления.

Матрица

называется матрицей тарифов,

– матрицей перевозок.

С целью удобства построения математической модели матрицы тарифов и перевозок совмещают в одну, именуемую макетом транспортной задачи (табл. 1).

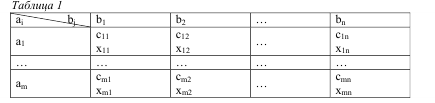
минимизируется при ограничениях:

на возможности поставщиков – весь продукт из пунктов производства должен быть вывезен:

3. ЭММ задачи распределения производственной программы предприятия.

В задаче о наилучшем использовании ресурсов определяется оптимальный план выпуска продукции.

Пусть при производстве какого-то общественно необходимого продукта используется п технологий.

При этом требуется т видов ресурсов, заданных объемами

bi (i =1,m ).

Эффективности технологий, т. е. количество конечной продукции (в ден. ед.), производимой в единицу времени по j-й ( j = 1,n ) технологии, обозначим cj .

Пусть, далее, aij – расход i-го ресурса в единицу времени по j-й технологии.

В качестве неизвестной величины xj примем интенсивность использования j-й технологии, т.е. время, в течение которого продукция производится по j-й технологии. Пренебрегая временем переналадок, необходимым для перехода от одной технологии к другой, получаем следующую математическую модель задачи: найти план интенсивностей использования технологий x* = (x1;...; xj;...; xn), обеспечивающий максимум выпуска продукции в стоимостном выражении:

4. ЭММ задачи оптимизации состава промышленных смесей.

В различных отраслях народного хозяйства возникает проблема составления таких рабочих, смесей на основе исходных материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе задач относятся задачи о выборе диеты, составлении кормового рациона в животноводстве,

шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности, смесей для получения бетона в строительстве и т. д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигают на первый план следующую, задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.

Модель задачи о наилучшем составе смеси рассмотрим на примере задачи о диете.

Имеются пищевые продукты, известные под номерами 1,2,...,n.

Они содержат различные питательные вещества, обозначаемые номерами 1,2,,.. , m (углеводы, белки, жиры, витамины, микроэлементы и др.).

Единица j-гo продукта содержит aij единиц i-го питательного вещества. Для нормальной жизнедеятельности в заданный промежуток времени нужно потреблять не менее bi единиц i-го питательного вещества. Обозначим через cj стоимость единицы продукта j-гo вида. Требуется выбрать рацион минимальнойстоимости, содержащий необходимые количества питательных веществ. План задачи –

это количества xj продуктов каждого вида, обеспечивающие необходимое количество питательных веществ при минимальных затратах на исходные продукты.

5. ЭММ задачи раскроя материалов.

Суть задачи об оптимальном раскрое состоит в разработке таких технологически допустимых планов раскроя, при которых получается необходимый комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму.

Рассмотрим простейшую модель раскроя по одному измерению. Более сложные постановки ведут к задачам целочисленного программирования.

Модель задачи раскроя по одному измерению длинномерных материалов (прутков, труб, профильного проката и др.) может быть сформулирована так. Пусть имеется N штук исходного материала, длина каждой штуки равна L.

Нужны заготовки m видов, длины которых равны

li (i =1,m ).

Известна потребность в заготовках каждого вида, она равна bj.

Изучение вопроса раскроя (построение технологической карты раскроя) показывает, что можно выделить n приемлемых вариантов раскроя исходного материала длиной L на заготовки длиной li.

Обозначим через aij количество заготовок i-го вида, получаемое при раскрое единицы исходного материала по j-му ( j = 1,n ) варианту, cj – отходы при раскрое единицы исходного материала по j-му варианту.

План задачи x* = (x1;...; xj;...; xn),

где xj – количество единиц исходного материала, планируемое к раскрою по j-му варианту.

Функция цели — минимум отходов, получаемых при раскрое: