
10305
.pdf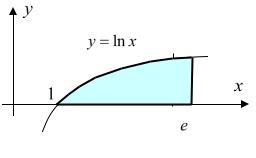
34.1.Интегрирование по частям и замена переменной. Пусть u(x)
иv(x) – функции, непрерывные вместе со своими производными в промежутке [ a,b] . Тогда функция F (x) u(x) v(x) является первообразной для
своей производной
|
F (x) u (x) v(x) v (x) u(x) . |
||||
По формуле Ньютона – Лейбница имеем |
|||||
|
b (u (x)v(x) v (x)u(x))d x u(x)v(x) |
|
ba |
||
|
|
||||
|
|
||||
|
a |
||||
откуда |
|
|
|
|
|
b |
|
|
b |
||
u(x)v (x)d x u(x)v(x) |
|
ba v(x)u (x)d x . |
|||
|
|||||
|
|||||
a |
|
|
a |
||
|
и |
|
|
|
|
Учитывая, что v (x)d x d v |
u (x)d x d u , полученную формулу запи- |
||||
шем более компактно, помня, что u и |
v функции переменной x , изменяю- |
||||
щейся в промежутке [ a,b] : |
|
|
|
|
|
|
|
b |
|
|
b |
|
|
udv uv |
|
ba vdu . |
|
|
|
|
|||
|
|
|
|||
|
|
a |
|
|
a |
Это и есть формула интегрирования по частям в определённом инте-
грале. Как и в случае неопределённого интеграла, её целесообразно применять, если интеграл справа будет «проще», чем исходный интеграл.
Пример. Найти площадь фигуры, ограниченной линией y ln x ,
осью абсцисс и прямой x e . Искомая площадь (см. рис. 34.1) выражается
e
интегралом S ln x d x
1
Рис. 34.1
240
Интегрируем по частям u ln x, |
du |
1 |
dx, dv dx, |
v x |
||||||
|
||||||||||
|
|
|
|
|
|
x |
|
|||
|
|
|
e |
1 |
|
|
|
|
|
|
S x ln x |
|
1e x |
d x e x |
|
1e e e 1 1. |
|||||
|
|
|||||||||
|
|
|||||||||
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формула Ньютона – Лейбница даёт возможность установить правило замены переменной в определённом интеграле. Пусть требуется вычис-
лить интеграл
b
f (x)d x ,
a
где функция f (x) непрерывна в промежутке |
[ a,b] . Пусть функция |
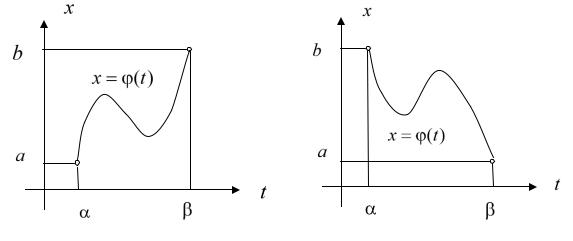
x (t) удовлетворяет следующим условиям: 1) |
(t) непрерывна вместе |
со своей производной (t) в некотором промежутке [ , ]; 2) сложная функция f ( (t)) должна быть определена в этом промежутке (для этого достаточно, например, потребовать, чтобы (t) была монотонна); 3) концам промежутка [ , ] соответствуют концы промежутка [ a,b] , т.е. ( ) a,( ) b или ( ) b , ( ) a (см. рис. 34.2).
Рис. 34.2
При этих условиях имеют место формулы
b |
|
f (x)d x f ( (t)) (t)d t |
|
a |
|
|
(34.1) |
b |
|
f (x)d x f ( (t)) (t)d t |
|
a |
|
|
241 |

Приведём доказательство первой из них. Пусть F (x) – одна из перво-
образных функции f (x) . |
Тогда F ( (t)) – первообразная функции |
|
f ( (t)) (t) . Действительно, |
|
|
F ( (t)) F |
( (t)) (t) f ( (t)) (t) . |
|
t |
|
|
Применяя формулу Ньютона – Лейбница к обоим интегралам в первом из
b
равенств (34.1), получим, с одной стороны, f (x)d x F (b) F (a) , а с дру-
a
гой
f ( (t)) (t)d t F ( (t) F ( ( )) F ( ( )) F (b) F (a) .
Аналогично можно убедиться в справедливости второго равенства в (34.1). Следует заметить, что, в отличие от замены переменной в неопределённом интеграле, здесь нет необходимости возвращаться к «старой» переменной. Если вычислены правые из интегралов (34.1), то, тем самым, вычислены и левые интегралы. Излишне упоминать, что не каждая подстановка ведёт к упрощению: какую замену переменной следует применять –это мо-
жет подсказать лишь опыт.
Пример. Вычислить площадь, ограниченную эллипсом, заданным
уравнением |
x2 |
|
y2 |
1. Ясно, что достаточно вычислить площадь четвёр- |
|||||
a2 |
b2 |
||||||||
той части фигуры. Задача приводит к вычислению интеграла |
|||||||||
|
|
|
|
a |
|
|
|
||
|
|
|
|
|
x2 |
||||
|
|
|
|
Sэл 4b |
1 |
|
|
|
dx . |
|
|
|
|
a |
2 |
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опыт вычисления неопределённых интегралов «подсказывает» замену переменной x(t) a sin t . Она удовлетворяет перечисленным выше условиям:
|
x(t) и x (t) a cost непрерывны в промежутке |
[0, / 2] |
||||||||||||||
|
x(0) 0, |
x( / 2) a |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
функция |
1 x2 (t) |
a2 |
1 sin2 t cost |
определена в [0, / 2] . |
|||||||||||
Произведя эту замену, получаем |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
S |
эл |
4b |
|
cos2t dt 2ab |
|
(1 |
cos 2t )dt ab . |
|||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
242 |
|
|
|
|
|
|
|

34.2. Вычисление площади фигуры в полярной системе координат.
Аналогом криволинейной трапеции в полярной системе координат будет
криволинейный сектор. Это фигура, ограниченная лучами , |
|
||
и кривой AB , заданной уравнением ( ) , определяющим для каждого |
|||
значения угла |
|
расстояние от начала координат до соответствующей |
|
точки кривой |
AB |
(см. рис. 34.3). |
|
Рис. 34.3
Предполагается, что функция ( ) непрерывна в промежутке, . Будем сначала решать задачу вычисления площади криволинейного сектора OAB приближённо. Для этого разобьём отрезок , на n частей
1 2 n n 1 .
Тогда «большой» криволинейный сектор разобьётся на n «узеньких» секторов. Обозначим k k 1 k . Заменим каждый «узенький» криволи-
нейный сектор круговым сектором, радиус которого примем равным( k ) , k [ k , k 1] . Площадь кругового сектора радиуса R и с центральным углом равна
Sсект. 12 R2 .
Поэтому площадь сектора OAB приближённо выражается интегральной суммой
S1 n 2 ( k ) k .
2 k 1
Переходя к пределу при n , причём так, что длина максимального из
частичных отрезков max( k ) стремится к нулю, получаем
k
243
|
1 |
n |
|
|
1 |
|
|
|
S lim |
2 ( k ) k |
|
2 ( )d . |
|||||
|
|
|||||||
n |
2 k 1 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
Замечание. Если начало координат находится внутри области, ограни- |
||||||||
ченной замкнутой кривой ( ) , |
0 2 , то площадь вычисляется по |
|||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|||
|
|
S |
2 ( )d . |
|
||||
|
|
2 |
|
|||||
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
||
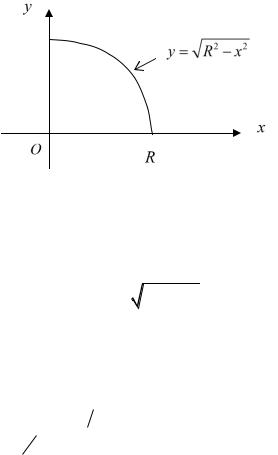
Пример 1. Вычислить площадь круга, граница которого задана уравнением x2 y2 R2 . Ясно, что достаточно найти площадь четверти круга
(см. рис. 34.4).
Рис. 34.4
Если вычисления проводить в декартовой системе координат, то получается «плохой» интеграл
1 |
R |
|
|
|
Skp |
R2 x2 dx . |
|||
4 |
||||
0 |
|
|
||
|
|
|
||
Перейдём к полярным координатам по формулам: x cos , y sin . Уравнение четвёртой части окружности x2 y2 R2 в полярных координа-
тах примет вид R, |
|
0 2 . Поэтому |
|
||||||||
|
|
|
|
|
|
|
|
|
|
R2 |
|
1 |
|
1 |
2 |
1 |
|
|
2 |
|
|||
|
|
Skp |
|
R2d |
|
R2 |
|
|
|
|
Skp R2. |
|
4 |
2 |
2 |
|
0 |
4 |
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
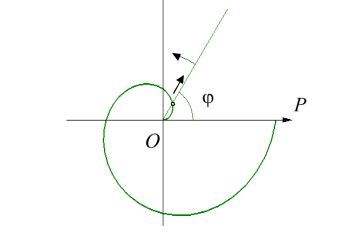
Пример 2. Вычислить площадь, |
ограниченную одним витком спи- |
||||||||||
рали Архимеда и полярной осью. Спираль Архимеда можно рассматривать как траекторию точки, равномерно движущуюся по лучу, исходящему из полюса, в то время как этот луч равномерно вращается вокруг полюса. В полярной системе координат её уравнение имеет вид a ,
244
a 0, a const . Один виток спирали получается при повороте луча на угол2 . Искомая площадь выражается интегралом
|
1 |
2 |
|
|
a |
2 |
|
3 |
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
2 |
3 |
|
|||
S |
|
(a ) |
|
d |
|
|
|
|
|
|
|
|
a |
|
. |
2 |
|
2 |
3 |
|
|
3 |
|||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 34.5
34.3. Вычисление площади фигуры, ограниченной кривыми, за-
данными параметрически. Интерпретируя определённый интеграл площадью криволинейной трапеции, мы предполагали, что кривая y f (x) за-
дана в явном виде. А как быть, если границы фигуры заданы параметрическими уравнениями? Заметим, что задание кривой в явном виде – это частный случай её параметрического задания, когда в качестве параметра избрана переменная x :
x x |
a x b . |
|
|
y f (x) |
|
В выборе параметра мы располагаем большой свободой. Например, при вычислении площади эллипса мы представляли его уравнение в параметрическом виде следующим образом:
x a sin t |
0 t |
|
. |
|
|
||
y b cost |
|
2 |
|
Таким образом, замена переменной в определённом интеграле – это, по сути, переход к другой параметризации кривой y f (x) . Поэтому, если
часть кривой, площадь под которой нас интересует, задана параметрически, то применяется формула
b |
|
x x(t) |
|
|
|
t . |
|
|
|
||
S y(x)dx y(t)x (t)dt , где |
|||
a |
|
y y(t) |
|
|
245 |
|
|
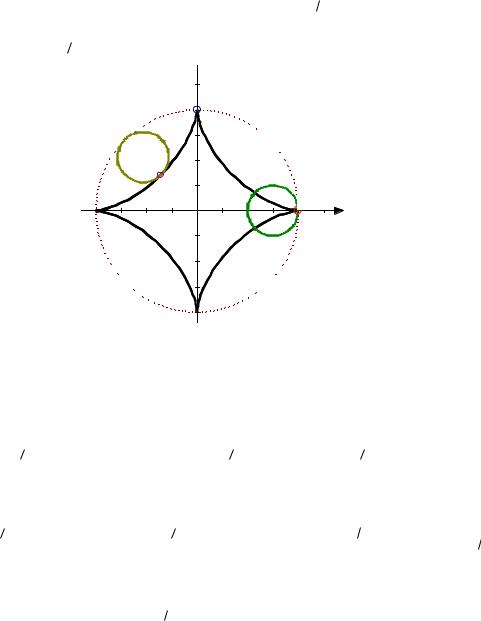
Пример 3. Найти площадь, ограниченную астроидой, заданной уравнениями
x a cos3 t |
|
|
|
|
0 |
t 2 |
|
y asin3 t |
|||
|
|
||
|
|
|
|
|
|
|
Астроиду можно рассматривать как траекторию фиксированной точки окружности, катящейся изнутри по окружности радиуса a и имеющей радиус a / 4 (см. рис. 34.6). В силу симметрии фигуры, вычисляем четвёртую часть её площади
1 |
a |
0 |
2 |
|
S y(x)dx |
asin3 t 3acos2t( sin t)dt 3a2 |
sin2 t cos2t sin2 tdt |
||
4 |
||||
0 |
2 |
0 |
||
|
 Y t=pi/2
Y t=pi/2
|
t=0 X |
0 |
a |
Рис. 34.6
После применения формул понижения степени тригонометрических функций получим
1 |
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
||
S |
|
a |
2 |
sin |
2 |
2t (1 cos2t)dt |
a |
2 |
sin |
2 |
2t dt |
|
a |
2 |
sin |
2 |
2t cos 2tdt |
|
||||||||||||||||||||||||
4 |
8 |
|
|
|
8 |
|
|
8 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
3 |
|
|
|
0 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
a2 |
|
|
(1 cos4t)dt |
|
a2 |
sin2 |
2t d sin 2t |
|
|
a2t |
|
|
|
a2 sin 4t |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
16 |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
16 |
|
|
|
0 |
|
64 |
|
|
|
||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
a2 sin3 2t |
|
2 |
|
a2 |
S |
a2 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Лекция 35. Другие приложения определённого интеграла
246
В предыдущей лекции мы применили определенный интеграл к вычислению площадей фигур. Здесь будут рассмотрены другие его приложения.
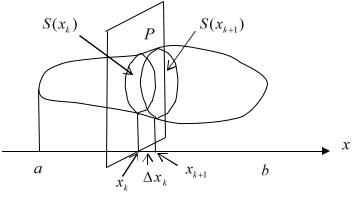
35.1. Вычисление объёма тела с известной площадью поперечного сечения. Пусть некоторое тело в направлении оси абсцисс находится в пределах отрезка [ a,b] . Как обычно, разбиваем этот отрезок на n частей и
через точки деления проводим плоскости P , перпендикулярные оси Ox . Эти плоскости рассекут тело на «дольки». На рисунке изображена одна из них.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 35.1 |
|
|
|
|
|
|||||
Предполагается, что для каждого значения x |
известна площадь |
сечения |
|||||||||
S(x) . Предполагается, что это непрерывная |
функция. Объём |
каждой |
|||||||||
«дольки» можно приближённо вычислить как объём цилиндра с площадью основания S (xk ) и высотой xk . Поэтому объём тела приближённо равен
сумме объёмов таких цилиндров
n
V S (xk ) xk
k 1
Точное значение объёма получим, увеличивая число n точек деления от-
резка [ a,b] . При этом длина наибольшего из отрезков max( xk ) должна
k
стремиться к нулю, т.е. находим предел интегральной суммы
|
n |
|
|
b |
|
V lim S (xk ) xk S (x)d x |
|||||
|
n k 1 |
|
|
a |
|
|
0 |
|
|
|
|
Пример. Найти объём части кругового цилиндра x2 y2 R2 , отсе- |
|||||
чённого плоскостями x 0, |
z 0, |
z |
h |
y . |
|
R |
|||||
|
|
|
|
||
247

Рис. 35.2
Через фиксированную точку x 0, R проводим плоскость, перпендику-
лярно оси Ox . Сечение тела представляет собой прямоугольный треугольник, площадь которого
|
1 |
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S (x) |
|
|
R |
x |
|
|
R |
2 |
x |
2 |
|
|
(R |
2 |
x |
2 |
) . |
|
|
|||||||||||
2 |
|
|
|
|
|
R |
|
|
|
|
2R |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда объём |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V R S (x)d x |
|
h |
R |
(R2 x |
2 )d x |
|
h |
|
(R2 x |
x3 |
) |
|
R |
|
1 |
hR2 . |
||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
0 |
|
|
2R |
0 |
|
|
|
|
|
|
|
|
2R |
|
|
3 |
|
|
0 |
|
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
35.2. Вычисление объёмов тел вращения. Пусть криволинейная тра- |
||||||||||||||||||||||||||||||
пеция, ограниченная кривой y f (x) , |
|
a x b , вращается относительно |
||||||||||||||||||||||||||||
оси Ox . Найдём объём полученного тела вращения.
Рис. 35.3
Поскольку нам известна площадь поперечного сечения тела для каждого
значения x , а именно (сечение – круг): |
S(x) f 2 (x) , то |
b |
b |
Vx S(x)d x f 2 (x)d x . |
|
a |
a |
248
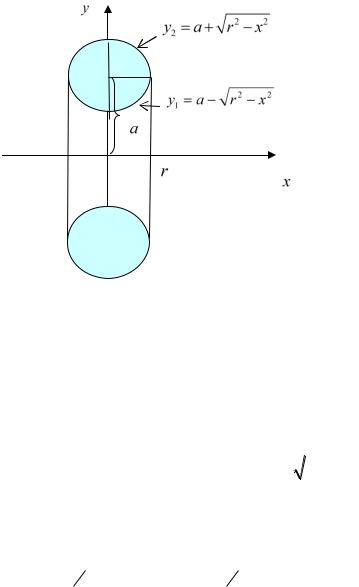
Пример. Найти объём тора («баранки»). Тор можно получить, вращая относительно оси Ox окружность x2 ( y a)2 r2
Рис. 35.4
Интересующий нас объём равен разности объёмов, полученных при враще-
нии кривых y1 |
|
и y2 . Поскольку фигура симметричная, то можно вычис- |
||||||||||||||
лять половину объёма |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
r |
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
V ( y22 |
y12 )d x ( y1 y2 )( y1 y2 )d x 4a |
|
r2 x2 d x |
|
|||||||||||
2 |
|
|||||||||||||||
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Применим подстановку |
x r sin t . |
Тогда будем иметь |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
V 4a r2 2 cos2 (t)d t 2a r2 |
2 |
(1 cos 2t)dt |
|
||||||||
|
|
|
2 |
|
||||||||||||
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a r2 (t |
1 |
sin 2t) |
2 |
a 2r2 . |
|
V |
2 2ar2. |
|
||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
тора |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35.3. Несобственные интегралы. Вводя определённый интеграл как |
||||||||||||||||
предел интегральных сумм |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
b |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
f (x)dx lim |
f (xk ) xk , |
|
max xk , |
(35.1) |
|||||||
|
|
|
|
|
a |
|
|
n k 1 |
|
k |
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
249 |
|
|
|
|
|
|
