
10290
.pdf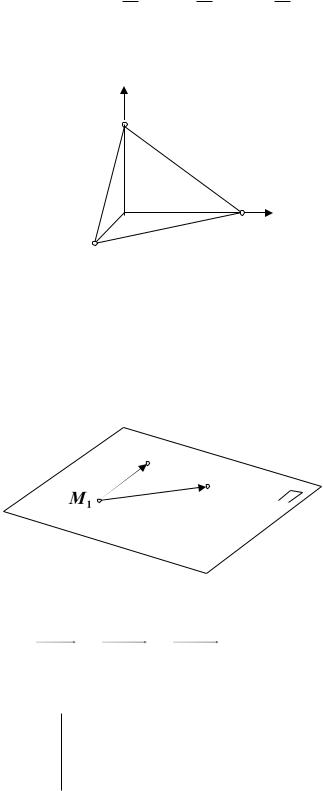
где (a,0,0) , (0,b,0) и (0,0,c) – точки пересечения плоскости с координатными осями. Действительно, из (11.2) следует Ax By Cz D и
далее, предполагая, что D 0 (т.е. плоскость не проходит через начало координат) и разделив обе части этого уравнения на D , получим
уравнение (11.3), в котором a DA , b DB и c CD величины отрезков,
которые плоскость «отрезает» от осей координат (см. рис. 11.6).
z
c
b
y
x  a
a
Рис. 11.6
Получим уравнение плоскости, проходящей через три заданные
точки M1 (x1, y1, z1 ) , M 2 (x2 , y2 , z2 ) , M 3 (x3 , y3 , z3 ) . Пусть |
M (x, y, z) – |
произвольная точка плоскости П . |
|
M2
M
 M3
M3
Рис. 11.7
Тогда три вектора M1M , M1M 2 , M1M 3 будут компланарными и, следовательно, их смешанное произведение равно нулю
x x1 |
y y1 |
z z1 |
|
|
|||
x2 x1 |
y2 y1 |
z2 z1 |
0 . |
x3 x1 |
y3 y1 |
z3 z1 |
|
|
80 |
|
|
Раскладывая этот определитель по элементам первой строки, приведем его к линейному уравнению относительно x, y, z вида (11.2).
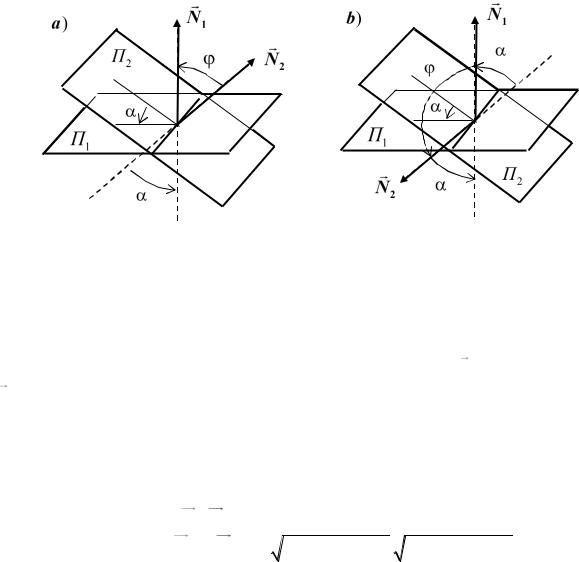
11.2. Взаимное расположение двух плоскостей. Пусть заданы две плоскости П1 и П2 уравнениями(см. рис. 11.8).
A1x B1 y C1z D1 0 , A2 x B2 y C2 z D2 0 .
Рис. 11.8
Найдем угол между ними в предположении, что они пересекаются. Пересекаясь, плоскости образуют две пары равных двугранных углов.
Углом между плоскостями |
|
П1 |
и П2 будем считать меньший из этих |
|||||||||
двугранных углов (см. рис. 11.8).Выразим угол |
|
между плоскостями |
||||||||||
через угол между нормальными к ним векторами |
N1 A1, B1,C1 и |
|||||||||||
N2 A2 , B2 ,C2 . Если угол |
острый, то |
(как углы с взаимно |
||||||||||
перпендикулярными сторонами). Если же угол |
|
– тупой, то |
||||||||||
(см. рис. 11.8 b) ), поэтому cos cos . В итоге |
для вычисления угла |
|||||||||||
между плоскостями имеем формулу |
|
|
|
|
|
|
|
|
||||
|
| N1, N 2 | |
| A1 A2 B1B2 C1C2 | |
||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||
| N1 | | N 2 |
| |
A12 B12 |
C12 |
A12 B12 C12 |
||||||||
В частности, условие перпендикулярности и условие параллельностидвух плоскостейимеют вид
П1 П2 A1 A2 B1B2 С1С2 0 ;
81

П1 П2 A1 B1 С1 . A2 B2 С2
В последнем случае, если дополнительно выполняется равенство
A1 |
|
B1 |
|
C1 |
|
D1 |
, |
(11.4) |
|
A2 |
B2 |
C2 |
D2 |
||||||
|
|
|
|
|
то эти плоскости совпадают.
Аналогично понятию пучка прямых на плоскости существует понятие
пучка плоскостей, проходящих через линию пересечения двух заданных плоскостей.В частности, им удобно пользоваться, когда нужно найти плоскость, проходящую через линию пересечения данных плоскостей и удовлетворяющую некоторому дополнительному условию. Уравнение пучка плоскостей имеет вид
( A1x B1 y C1z D1 ) ( A2 x B2 y C2 z D2 ) 0 . (11.5)
Действительно, уравнение (11.5) – уравнение плоскости. Так как координаты любой точки, принадлежащей линии пересечения П1 и П2 ,
обращают в ноль обе скобки в (11.5), то при любом эта плоскость проходит через линию пересечения этих плоскостей.
11.3. Расстояние от точки до плоскости. Пусть требуется вычислить расстояние отточки M 0 (x0 , y0 , z0 ) до плоскости Ax By Cz D 0 .
Рис. 11.9
82

Пусть M1 (x1, y1, z1 ) – проекция точки M 0 наданную плоскость(см. рис. 11.9). Искомое расстояние равно абсолютной величине проекции вектора M1M 0 на направление нормального вектора N A, B,C :
d |
|
ПрN M1M 0 |
|
|
| N ,M1M 0 |
|
| |
|
|
|
A( x0 x1 ) B( y0 y1 ) C( z0 z1 ) |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| N | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Ax0 By0 |
|
Cz0 |
Ax1 By1 Cz1 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как точка |
M1 (x1, y1, z1 ) |
|
принадлежит плоскости, то Ax1 By1 Cz1 |
D |
||||||||||||||||||||||||||||||||||||||
,поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
d |
|
|
Ax0 |
|
By0 |
Cz0 D |
|
. |
|
|
|
|
|
|
|
(11.6) |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Найдём координаты точки M1 (x1, y1, z1 ) . Для этого выразим вектор |
||||||||||||||||||||||||||||||||||||||||||
M1M 0 через |
найденное |
|
|
расстояние d и |
единичный |
вектор |
|
1 |
|
|
N , |
|||||||||||||||||||||||||||||||
|
|
| N | |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нормальный кплоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
M1M 0 |
d |
|
N . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.7) |
|
|
|
|
|
||||||||||||||
|
|
|
| N | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из формулы (11.6) видно, что знак проекции вектора |
M1M 0 |
|||||||||||||||||||||||||||||||||||||||||
определяетсязнаком |
|
|
выражения Ax0 By0 |
Cz0 D , |
т.е., |
если |
||||||||||||||||||||||||||||||||||||
Ax0 By0 Cz0 |
D 0 , то |
|
|
M1M 0 N , |
и в формуле (11.7) нужно взять |
|||||||||||||||||||||||||||||||||||||
знак «плюс». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример.Найти проекцию начала координат на плоскость |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 2 y z 7 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Пусть M1 (x1, y1, z1 ) – |
|
проекция |
|
|
|
|
точки (0,0,0) наданную |
плоскость(см. |
||||||||||||||||||||||||||||||||||
рис.11.10). Вычисляем расстояние точки (0,0,0) до плоскости |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
d |
|
|
|
3 0 2 0 1 0 7 |
|
|
|
|
7 |
|
|
1.9 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 4 9 |
|
|
|
14 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Отсюда следует, что |
M1O { x1, y1, z1} N {3, 2, 1} |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
83 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
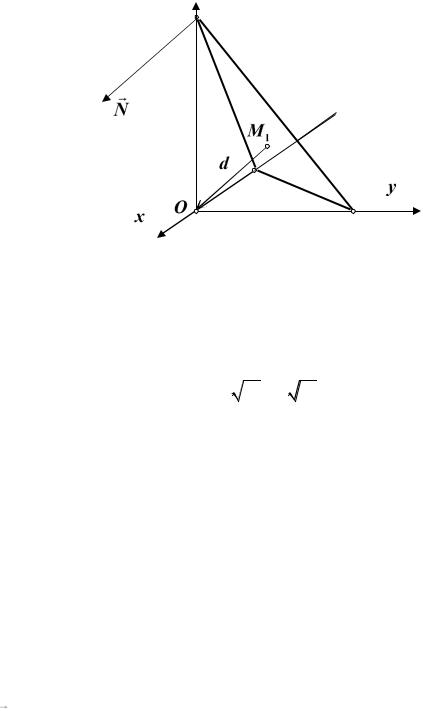
z
Рис. 11.10
Из равенства (11.7), взятого со знаком плюс, имеем
{ x , y , z } |
|
7 |
|
|
{3, |
2, 1} |
. |
|||
|
|
|
|
|
|
|||||
1 |
1 |
1 |
14 |
14 |
|
|
||||
|
|
|
|
|
||||||
Отсюда находим M1 ( 1.5,1,0.5) .
Лекция 12. Прямая линия в пространстве
12.1. Различные виды уравнений прямой. Пусть в трехмерном пространстве с декартовой прямоугольной системой координат имеем прямую L , и мы хотим получить уравнение, связывающее координаты любой её точки. Пусть M 0 (x0 , y0 , z0 ) – некоторая фиксированная точка этой
прямой и S {m, n, p} – вектор, параллельный прямой L , называемый
направляющим вектором этой прямой
84
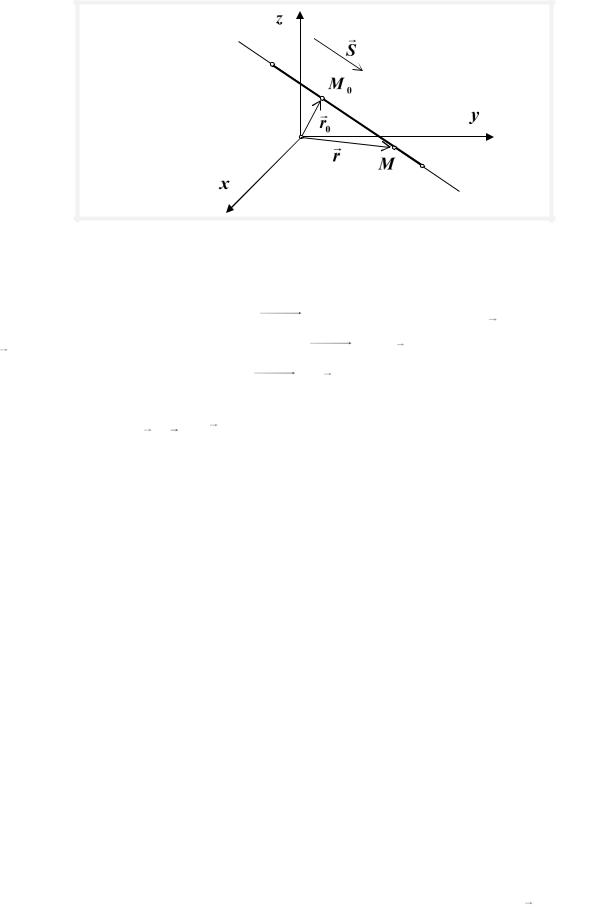
|
|
Рис. 12.1 |
|
Возьмем на прямой |
L произвольную точку |
M (x, y, z) . Рассмотрим |
|
следующие |
векторы |
M0M {x x0 , y y0 , z z0}, r {x0 , y0 , z0}и |
|
r {x, y, z}. |
Очевидно, |
что векторы M 0M и S |
коллинеарны, поэтому |
существует число t такое, что M0M t S , т.е. |
|
||
|
r r0 t S . |
(12.1) |
|
Записывая равенство (12.1) в координатах, получим так называемые
параметрические уравнения прямой в пространстве
x x0 |
mt |
|
|
|
|
y y0 nt |
(12.2) |
|
|
p t |
|
z z0 |
|
|
Ясно, |
что при изменении значения параметра t |
в пределах от |
до |
точка |
M (x, y, z) «пробегает» всю прямую L . |
В частности, при |
t 0 |
уравнения (12.2) дают координаты точки M 0 (x0 , y0 , z0 ) .
Выразим параметр t из каждого уравнения (12.2), приравняем друг другу полученные выражения и придем к так называемым каноническим
уравнениям прямой в пространстве |
|
|
|||||||
|
x x0 |
|
y y0 |
|
z z0 |
. |
|
(12.3) |
|
|
|
|
|
|
|
||||
|
m |
|
n |
|
p |
|
|
|
|
Заметим, |
чтона |
плоскости |
xOy |
каноническое |
уравнение прямой, |
||||
проходящей через точку M 0 (x0 , y0 ) с направляющим вектором S {m, n} , имеет вид
85
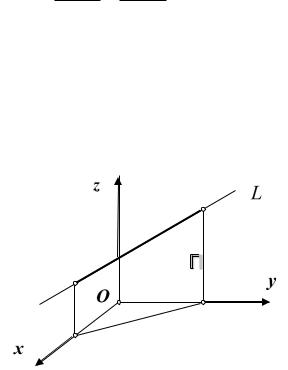
x x0 y y0 .(12.4) m n
Обратим внимание, что уравнения (12.3) представляют собой краткую запись трёх равенств. Рассмотрим, например, одно из них(12.4). Это уравнение плоскости, параллельной оси O z . Так как координаты любой
точки прямой (12.3) удовлетворяют уравнению (12.4), то прямая L лежит в этой плоскости
Рис.12.2
Линия пересечения плоскости (12.4) с плоскостью xOy является проекцией
прямой L на эту координатную плоскость.
Рассматривая совместно пару равенств из (12.3) , например,
x x |
|
|
|
y y |
|
||||
|
0 |
|
|
|
|
0 |
|
|
|
|
m |
|
n |
|
|
|
|||
|
|
|
|
|
|
|
, |
||
x x |
|
|
|
z z |
|
|
|||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
m |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим уравнение прямой L в виде линии пересечения двух плоскостей.
В общем случае уравнения прямой как линии пересечения двух непараллельных плоскостей П1 и П2 имеют вид
A1x B1 y C1z D1 |
0 |
(12.5) |
|
|
|
A2 x B2 y C2 z D2 |
0 |
|
Приведём конкретный пример задания прямой в таком виде (см. рис. 2.3).
86
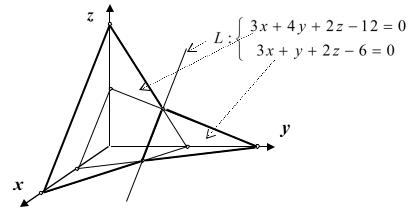
Рис. 12.3
Выше был показан переход от канонических уравнений прямой к уравнениям вида (12.5). Покажем, как из уравнений (12.5) получить канонические уравнения этой прямой. Для этого надо найти какую-нибудь одну точку прямой L и её направляющий вектор. Для нахождения координат точки решим систему двух уравнений (12.5) относительно двух переменных, коэффициенты перед которыми образуют базисный минор, фиксируя при этом третью переменную. Совместность этой системы уравнений, а значит, и наличие такого минора, гарантируется предположением о том, что плоскости П1 и П2 не параллельны. Пусть, например,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
B1 |
0 , |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
B2 |
|
|
|
|
|
|
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
C1z D1 |
B1 |
|
|
|
|
|
|
A1 |
C1z D1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x |
|
|
C2 z D2 |
B2 |
|
|
, |
y |
|
|
A2 |
C2 z D2 |
|
|
. |
(12.6) |
|||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Раскрывая определители в этих выражениях, представим решения |
|||||||||||||||||||||
системы (12.5) в виде |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x z , |
y z . |
|
||||||||
|
Будем рассматривать переменную |
z в качестве параметра, выразим её |
||||||||||||||||||||
из полученных равенств и запишем их в виде |
|
|||||||||||||||||||||
|
x |
|
|
y |
|
z |
. |
|
|
|
|
|
(12.7) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, координаты точек прямой L , заданной уравнениями (12.5), удовлетворяют уравнениям (12.7), которые можно рассматривать как
87
канонические уравнения этой прямой. В частности, точка ( , ,0) лежит на
этой прямой, а S { , ,1} – её направляющий вектор.
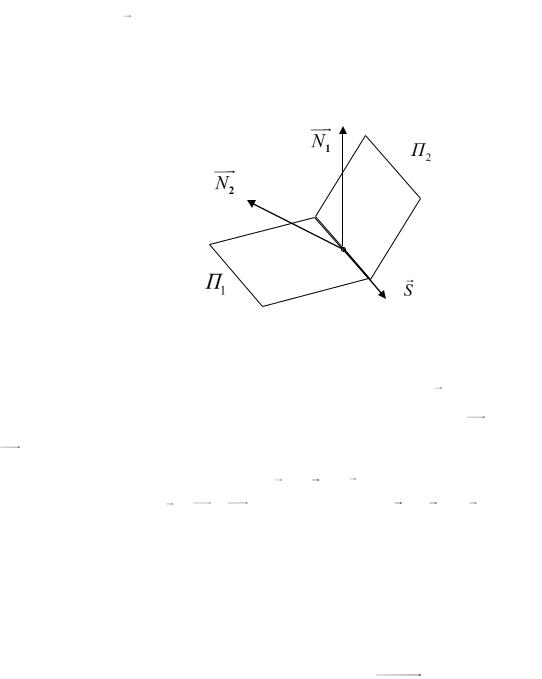
Возможен и другой путь получения канонических уравнений прямой из уравнений прямой как линии пересечения двух плоскостей П1 и П2 ,
заданных уравнениями (12.5)
|
|
Рис. 12.4 |
|
|
|
|
Очевидно, что в качестве направляющего вектора S {m, n, p} прямой |
L |
|||||
можно взять векторное произведение |
векторов |
N1 {A1, B1,C1} |
и |
|||
N2 {A2 , B2 ,C2}, т.е. |
|
|
|
|
|
|
|
i |
j |
k |
|
|
|
|
|
|
|
|||
S N1 N2 |
A1 |
B1 |
C1 |
mi n j pk , |
|
|
|
A2 |
B2 |
C2 |
|
|
|
|
|
|
|
|
|
|
а координаты какой-нибудь точки этой прямой получим, решая систему (12.5) при фиксированном значении переменной z (например, z 0 ).
Получим уравнения прямой в пространстве, проходящей через две заданные точки M1 (x1, y1, z1 ) и M 2 (x2 , y2 , z2 ) . Очевидно, что направляющим
вектором этой прямой может служить вектор |
M1M2 {x2 x1, y2 y1, z2 z1} |
||||||
, и тогда канонические уравнения примут вид |
|
||||||
|
x x1 |
|
y y1 |
|
z z1 |
. |
(12.8) |
|
|
|
|
||||
|
x2 x1 |
y2 y1 |
z2 z1 |
|
|||
12.2. Проекция точки на прямую и расстояние от точки до прямой в пространстве. Пусть прямая задана каноническими уравнениями
x x1 |
|
y y1 |
|
z z1 |
. |
|
|
|
|||
m |
|
n |
|
p |
|
88
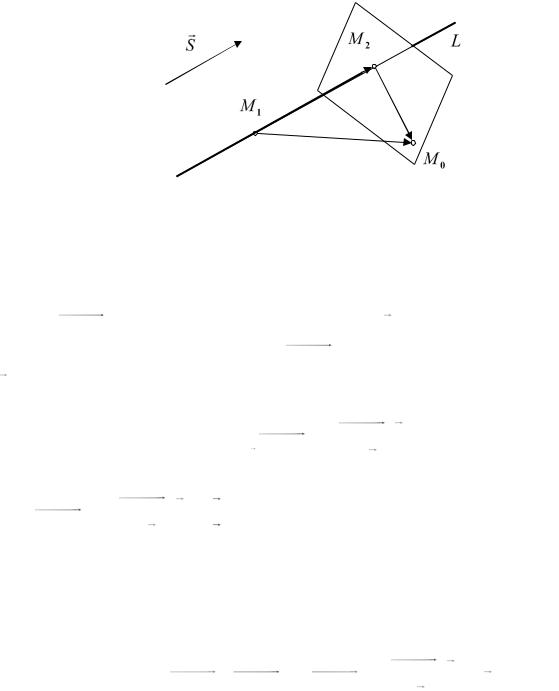
Обозначим через |
M 2 (x2 , y2 , z2 ) проекцию точки |
M 0 |
на данную |
прямую (см. рис. 12.5). Напомним, что проекцией точки M на ось L в |
|||
пространстве называется |
точка M1 пересечения оси |
L и |
плоскости, |
проходящей через точку |
M 0 перпендикулярно этой оси. |
|
|
Рис.12.5
Требуется найти координаты точки M 2 и расстояние от точки M 0 (x0 , y0 , z0 ) до этой прямой. Искомая точка будет найдена, если мы найдем
вектор M1M 2 , который коллинеарен |
вектору S {m, n, p} |
и имеет длину, |
|||||||||
равную модулю проекции вектора M1M0 {x0 x1, y0 y1, z0 |
z1} на вектор |
||||||||||
S . Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПрS M1M0 |
|
M1M0 |
, S |
, |
|
|
|
|
|
|
|
| S | |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
M1M2 |
|
M1M0 |
, S S |
.(12.9) |
|
|
|
|
|
||
| S | |
|
|
|
|
|
|
|
|
|||
|
|
|
| S | |
|
|
|
|
|
|||
Поэтому искомое расстояние вычисляется по формуле
d | M1M0 M1M2 | | M1M0 M1M0 , S S | . | S |2
Пример. Вычислить расстояние точки M 0 (2, 1,3) до прямой
89
