
6762
.pdf
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
7.1. cos2 2x =1+ sin 22x ; |
7.2. 4cos2 x = 3; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
7.3. 2cos2 x =1+ 2sin 2x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
7.4. 2 |
|
2 |
cos2 x =1+ |
2 . |
|
|
|
|
||||||||||||||||||
|
8. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
8.1. (1+ cosx)(3 − 2cosx)= 0; |
|
|
8.2. (1− cosx)(4 + 3cos2x)= 0; |
|
|||||||||||||||||||||||
|
8.3. (1+ 2cosx)(1− 3cosx)= 0; |
8.4. (1− 2cosx)(2 + 3cosx)= 0. |
|
|||||||||||||||||||||||||
|
9. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
9.1. arccos (2x − 3)= π ; |
|
9.2. arccos |
x +1 |
= |
|
2π |
. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
Ответы. 1.1.π ; 1.2. 0; 1.3. π ; 1.4. π ; 1.5. |
5π |
. 1.6. |
3π |
|
|
2.1. π ; 2.2. |
2π ; |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
2 |
|
4 |
|
|
3 |
|
6 |
4 |
|
|
|
|
|
|
|
|
||||||||||||
2.3.π ; 2.4. 8π . 3.1. |
x = ±π + 2πk , |
k Z; |
3.2. |
|
x = ± π + 2πn , |
n Z; |
3.3. |
|||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
x = ± |
5π |
+ 2πk, k Z; 3.4. x = ± |
3π |
+ 2πn , n Z. 4.1. x = ±arccos |
1 |
+ 2πk , k Z; |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
6 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||
4.2. x = ±arccos |
3 |
+ 2πk , |
k Z; |
4.3. |
x = ±(π − arccos0,3)+ 2πk , |
k Z; |
4.4. |
|||||||||||||||||||||
|
||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x = ±(π − arccos0,2)+ 2πk , |
k Z. 5.1. x = πk , |
k Z; 5.2. x = π +πn , n Z; 5.3. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
x = ±3π + 8πk , k Z; |
5.4. |
x = ±π + 6πn , n Z; 5.5. x = π + πk , |
k Z; |
5.6. |
||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
||||||
x = |
3π |
+ πn , |
n Z. 6.1. x = π + πk , k Z; 6.2. x = π +πn , n Z. |
7.1. x = πk , |
||||||||
|
||||||||||||
8 |
|
2 |
|
8 |
4 |
|
|
2 |
|
|
2 |
|
k Z; |
7.2. x = ± π + 2πn , |
x = ± |
5π |
+ 2πn , |
n Z; |
7.3. |
x = ± π + πk , |
k Z; |
7.4. |
|||
|
||||||||||||
|
|
|
|
6 |
|
6 |
|
|
|
6 |
|
|
x = ± π + πn , |
n Z. 8.1. |
x =π + 2πk, |
k Z; |
8.2. |
x = 2πn , |
n Z; |
8.3. |
|||||
8 |
|
|
|
|
|
|
|
|
|
|
||
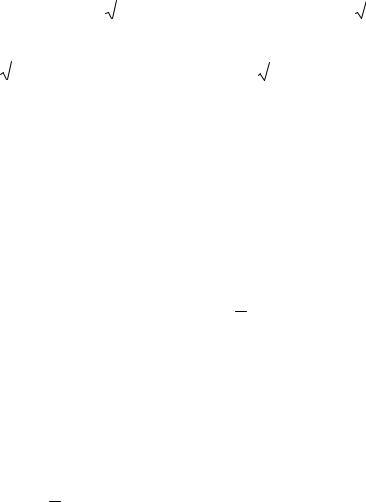
21
x |
|
= ± |
2π |
+ 2πk , |
k Z; |
x |
|
|
= ±arccos |
1 |
+ 2πn , |
n Z; 8.4. |
|
x = ± π + 2πn , |
n Z; |
|||||||||||||||||||||||||||||||||||||
1 |
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
+ 2πk , k Z. 9.1. x = |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x = ±arccos − |
|
|
|
|
|
|
; 9.2. x = −2,5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.2. Уравнение sinx = a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Уравнение |
sinx = a, если |
|
a |
|
≤1, имеет решения |
x = (−1)k arcsina + kπ , |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
k Z, |
где |
|
arcsina |
– |
|
арксинус числа |
а. Арксинусом |
числа |
(arcsina), |
где |
||||||||||||||||||||||||||||||||||||||||
|
|
|
a |
|
≤1, называется |
угол α такой, что 1) |
|
|
π |
; |
π |
|
|
и 2) синус которого |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
α − |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
равен а: sinα = a (arcsina =α , если sinα = a). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= π , |
|
|
|
|
|
|
sin π = |
|
|
|
|
|
|
|
− π ≤ π ≤ π ; |
||||||||||||||||||||||
|
|
|
|
|
Например, |
arcsin |
|
|
|
|
2 |
так |
|
|
как |
|
|
2 |
|
|
и |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
2 |
4 |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
π |
|
|
|
|
π |
|
π |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
arcsin |
− |
|
|
|
|
|
= − |
|
, так как sin |
− |
|
|
|
= − |
|
|
и − |
|
≤ |
− |
|
|
|
≤ |
|
. |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
2 |
|
|
|
3 2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
Тождества |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
sin(arcsina)= a , если |
|
а |
|
≤1; arcsin(sin x)= x , если |
|
|
|
|
π |
; |
π |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x − |
|
|
; |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
||||
arcsin(− a)= −arcsina .
Задача 1. Решить уравнение sin x = 1 .
2
Решение. sin x – ордината точки единичной окружности, полученной поворотом точки P(1;0) вокруг начала координат на угол x (рисунок 4.2).
Ординату равную |
1 |
|
имеют две точки окружности M1 и M2 (рисунок 4.2, |
|
|||
2 |
|
||
слева). Так как 1 = sin π , то точка M1 получается из точки P(1;0) поворотом
26
на угол |
x |
1 |
= π |
, а также на углы |
x = π + 2πk , где k Z. Точка |
M |
2 |
|
|
6 |
|
6 |
|
||
|
|
|
|
|
|
22
получается из точки P(1;0) |
поворотом на угол |
x |
|
= |
5π |
, а также на углы |
||||
2 |
|
|||||||||
|
|
|
|
|
|
|
6 |
|
||
|
|
|
|
|
|
|
|
|
||
x = |
5π |
+ 2πk , т.е. на углы x = π − π + 2πk , где |
k Z. Таким образом, все |
|||||||
|
||||||||||
6 |
|
|
|
6 |
|
|
|
|
|
|
корни уравнения sinx = |
1 |
|
можно найти по |
|
формулам x = π + 2πk , |
|||||
|
|
|||||||||
2 |
|
|
|
|
|
6 |
||||
x = π − π + 2πk , k Z. Эти формулы объединяются в одну x = (−1)k π + nπ , 6 6
n Z.
Рисунок 4.2. Тригонометрическая окружность с ординатами
точек M1 и M2
В самом деле, если n − чётное число, т.е. n = 2k , то x = π + 2πk , если 6
нечётное число, т.е. n = 2k +1, то x = π − π + 2πk , то есть x = 5π + 2πk. 6 6
Ответ.x = (−1)k π + nπ , n Z. 6
Задача 2. Решить уравнение sinx = − 1 .
2
Решение. Ординату равную − |
1 |
|
имеют две точки окружности M |
|
и |
|
1 |
||||
2 |
|
|
|||
|
|
|
|||
n −
M2
(рисунок 4.2, справа), |
где x |
|
= −π |
, x |
|
= − |
5π |
. Следовательно, все корни |
||
1 |
2 |
|
||||||||
|
|
|
|
6 |
|
6 |
|
|||
|
|
|
|
|
|
|
|
|||
уравнения sinx = − |
1 |
|
можно найти |
|
по формулам x = −π + 2πk и |
|||||
|
|
|||||||||
2 |
|
|
|
|
|
|
|
6 |
||

|
|
|
|
|
23 |
x = − |
5π |
+ 2πk , |
k Z. Эти формулы объединяются в одну |
||
|
|||||
6 |
|
|
|
|
|
|
n |
− |
π |
+ πn, n Z. |
|
x = (−1) |
|
||||
|
|
|
|
6 |
|
В самом деле, если n − чётное число, т.е. n = 2k , то x = −π + 2πk , k Z, 6
если n − нечётное число, т.е. n = 2k +1, то x = − 5π + 2πk , k Z. 6
Ответ. x = (−1)n+1 π + πn, n Z. 6
Итак, каждое из уравнений |
sinx = |
1 |
|
и sinx = − |
1 |
имеет бесконечное |
||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
множество корней. На интервале |
− π ≤ x ≤ π каждое из этих уравнений |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет только один корень: x |
|
= π |
− корень уравнения sinx = |
1 |
и x |
|
= −π − |
|||||||||||||||||||||||||||||
1 |
|
1 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
2 |
6 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
корень уравнения |
|
sinx = − |
1 |
. Число |
π |
называют арксинусом числа |
1 |
|
|
и |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
записывают arcsin |
1 |
= π ; число |
− π |
|
называют |
арксинусом числа |
− |
1 |
|
и |
||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
6 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
− |
1 |
|
|
= − |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пишут arcsin |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3. Решить уравнение sin x = |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Так |
|
как |
|
2 |
[−1;1], |
то |
уравнение |
sin x = |
2 |
имеет решения |
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
x = (−1)n arcsin 2 + πn , n Z. 3
Ответ. x = (−1)n arcsin 2 + πn , n Z. 3

|
24 |
Частные случаи |
|
|
|
sinx = 0, |
x =πn, n Z. |
|
|
sin x =1, |
x = π + 2πn, n Z. |
|
2 |
|
|
sinx = −1, |
x = −π + 2πn , n Z. |
|
2 |
|
|
Задача 3. Решить уравнение sin2 x =1.
Решение. 2x = π + 2πn , x = π + πn , n Z.
24
Ответ. x = π
4
Упражнения
1. Вычислить 1.1. arcsin 0;
1.4. arcsin 1 ; 2
+ πn , n Z.
1.2. arcsin 1; |
|
|
|
|
|
|
1.3. arcsin |
|
3 |
; |
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|||||||
1.5. arcsin |
|
− |
|
|
|
|
; |
1.6. arcsin |
|
− |
|
|
|
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. Вычислить
2.1. arcsin 1− arcsin (−1); |
|
|
|
1 |
|
|
|
|
1 |
|
|
|||||||||
2.3. |
arcsin |
|
|
|
|
+ arcsin |
− |
|
|
|
|
|
; |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
||||||
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|||||||||
2.2. arcsin |
|
+ arcsin |
|
|
; |
2.4. |
arcsin |
|
|
|
|
|
+ arcsin |
− |
|
|
. |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|||||
3. Решить уравнения |
|
|
|
|
|||
|
|
|
|
|
|
|
|
3.1. sin x = |
3 |
; |
3.2. sin x = |
2 |
; |
||
|
|
||||||
2 |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
3.3. sin x = − |
1 |
|
|
; |
3.4. sinx = − |
1 |
. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
4. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4.1. |
sinx = |
3 |
; |
|
|
|
4.2. sinx = |
2 |
; |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4.3. sinx = − |
; |
|
|
|
4.4. sin x = |
|
5 |
. |
|
|
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
3 |
|
|
|
|
|
|||||||||
5. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5.1. sin3x =1; |
|
|
5.2. sin2x = −1; |
|
||||||||||||||||||||||||
|
|
|
|
x |
|
= −1; |
5.4. 2sin |
x |
= |
|
|
|
|
|||||||||||||||
5.3. |
|
2 |
sin |
|
3; |
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
3π |
|
|
π |
|
|||||||||||||||
5.5. |
sin x |
+ |
|
|
|
|
|
|
|
|
= 0 |
5.6. sin 2x + |
|
|
|
|
= 0. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|
||||||||||||||
6. Решить уравнения
6.1.sin4 x cos 2x = cos4x sin2x ;
6.2.cos 2x sin3x = sin2x cos3x .
7. Решить уравнения |
|
|
|
|
|
|
|
|||||
7.1. |
1− 4sin xcosx = 0; |
|
|
|
|
|||||||
7.2. |
3 |
+ 4sin xcos x = 0 ; |
||||||||||
7.3. |
1+ 6sin |
x |
cos |
x |
= 0; |
7.4. 1− 8sin |
x |
cos |
x |
= 0 . |
||
|
|
|
|
|||||||||
|
4 |
4 |
|
3 |
3 |
|
||||||
8. Решить уравнения
8.1.1+ cos 5x sin4 x = cos4x sin5x ;
8.2.1− sin x cos2x = cos x sin2x .

|
26 |
9. Решить уравнения |
|
9.1. (sin x −1)(3sin x +1)= 0; |
9.2. (4sin x − 3)(2sin x +1)= 0; |
9.3. (2sin2x −1)(sin4x +1)= 0 ; |
9.4. (4sin3x −1)(2sin x + 3)= 0. |
10. Решить уравнения
|
x |
|
|
π |
|
10.2. arcsin (3 − 2x)= − |
π |
|
10.1. |
arcsin |
|
− 3 |
= |
|
; |
. |
|
|
|
|||||||
|
|
2 |
|
|
6 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
1.2. π ; 1.3. π ; 1.4. |
π ; 1.5. − |
|
|
|
|
; 1.6. − π . 2.1. π ; 2.2. 0; |
||||||||||||||||||||||||||||||||||
Ответы. 1.1. 0; |
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
6 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||
2.3. π ; |
2.4. |
|
− π . 3.1. x = (−1)k π + πk, k Z; |
3.2. |
|
x = (−1)n π + πn , |
n Z; 3.3. |
||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||
x = (−1)k+1 π + πk, k Z; |
3.4. |
x = (−1)n π + πn , |
n Z. 4.1. |
|
x = (−1)n arcsin |
3 |
|
+ πn , |
|||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||
n Z; 4.2. x = (−1)n arcsin |
2 |
+ πn , |
n Z; 4.3. x = (−1)n+1 arcsin |
1 |
+ πn, |
n Z; 4.4. |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
n Z. 5.1. x = π + |
2πk |
|
, k Z; 5.2. x = −π + πn , |
|
|
||||||||||||||||||||||||||||||||||
x = (−1)n arcsin |
|
|
5 |
+ πn , |
n Z; |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||||||
5.3. x = (−1)n+1 |
3π |
|
|
+ 3πn , |
n Z; 5.4. x = (−1)n |
2π |
+ 2πn , n Z; 5.5. x = − |
3π |
+ πn , |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||||
n Z; 5.6. |
|
x = −π + πn , |
n Z. |
6.1. x = πn , |
|
|
n Z; |
6.2. |
|
x =πn, |
n Z. |
7.1. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n π |
|
|
πn |
|
|
|
|
|
|
|
|
|
|
|
|
|
n+1 π |
|
πn |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x = (−1) |
|
|
|
+ |
|
|
, |
|
|
|
n |
Z; |
7.2. |
|
x = (−1) |
|
|
|
|
+ |
|
, |
|
|
|
|
n Z; |
|
|
|
7.3. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
12 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x = (−1)n+1 2arcsin |
1 |
+ 2πn , |
|
n Z; |
7.4. |
|
x = (−1)n |
3 |
arcsin |
1 |
+ |
3πn |
, |
n Z. |
8.1. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|||||||||||||||
x = π + πn , |
|
n Z; |
8.2. |
|
|
|
x = π + |
2πn |
, |
n Z. 9.1. |
x = (−1)n π + πn , |
n Z; |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|||||
x = (−1)k+1 arcsin |
1 |
+ πk , |
|
|
|
k Z; |
9.2. |
|
|
|
|
x = (−1)n+1 π + πn, |
|
|
n Z; |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
x = (−1)k arcsin |
3 |
+ πk , |
k Z; 9.3. |
x = (−1)n |
π |
+ πn , n Z; |
x = |
3π |
+ πn , n Z. |
|||||||
|
|
|
||||||||||||||
4 |
|
|
|
|
12 |
2 |
|
8 |
2 |
|||||||
|
|
|
|
|
+ πn , n Z. 10.1. x = 7; 10.2. x = |
6 + |
|
|
|
|
|
|||||
9.4. x = (−1)n |
1 |
arcsin |
1 |
|
2 |
. |
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
3 |
|
4 |
|
3 |
|
|
4 |
|
|
|
|
|
||||
4.3. Уравнение tgx = a
Уравнение tgx = a , a R , имеет решения x = arctga + kπ , k Z, где arctga – арктангенс числа а.
Арктангенсом числа (arctga), где a R , называется угол α такой, что
1)α − π ;π ,
2 2
2)tgα = a (arctga = α , если tgα = a ).
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
|
|
π |
|
π |
|
π |
|
|
|
|
3 |
|
|
|
π |
|
|
Например, arctg1= |
|
, так как |
tg |
=1 и |
− |
|
|
< |
|
< |
|
; arctg |
− |
|
|
|
|
|
= − |
|
, так |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
2 |
|
4 |
|
2 |
|
|
|
3 |
|
|
|
6 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
π |
|
|
|
|
|
π |
|
π |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
− |
< − |
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
как tg − |
= − |
|
|
|
и |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
6 |
3 |
|
|
|
2 |
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тождества |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
π |
; |
π |
; arctg(− x)= arctgx. |
|
|
|
|
|
|
|
||||||||
tg(arctga)= a ; arctg(tgx)= x , если x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, arctg(− 
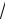 3)= −arctg
3)= −arctg
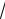 3 = −π ; arctg(−1)= −arctg1= −π .
3 = −π ; arctg(−1)= −arctg1= −π .
3 |
4 |
|||
|
|
|
||
Задача 1. Решить уравнение tgx = |
3 |
. |
|
|
|
|
|
||
Решение. Построим углы, тангенсы которых равны |
3 . Для этого |
|||
проведём через точку Р (рисунок 4.3.) прямую, перпендикулярную РО (ось тангенсов), и отложим отрезок PM = 
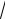 3 , через точки М и О проведём прямую. Эта прямая пересекает окружность в двух диаметрально противоположных точках M1 и M2 . Из прямоугольного треугольника РОМ находим
3 , через точки М и О проведём прямую. Эта прямая пересекает окружность в двух диаметрально противоположных точках M1 и M2 . Из прямоугольного треугольника РОМ находим
28
|
PM |
= |
|
|
3 |
= |
|
|
|
, откуда x |
|
= π |
. Таким образом, точка M |
|
|
|||||||
|
|
|
3 |
= tgx |
1 |
1 |
1 |
получается из |
||||||||||||||
|
|
|
||||||||||||||||||||
|
PO |
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
точки P(1;0) |
|
поворотом вокруг начала координат на угол π , а также на углы |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||
|
x = π + 2πk, где k Z. |
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Точка |
M |
2 |
получается поворотом точки P(1;0) на угол x |
2 |
= π + π , а также |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на углы x = π + π + 2πk , где k Z. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, корни уравнения tgx = |
|
|
можно найти по формулам x = π + 2πk, |
||||||||||||||||
|
|
|
|
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x = π + π (2k +1), k Z. Эти формулы объединяются в одну: x = π + πn , n Z. 3 3
Ответ. x = π + πn , n Z. 3
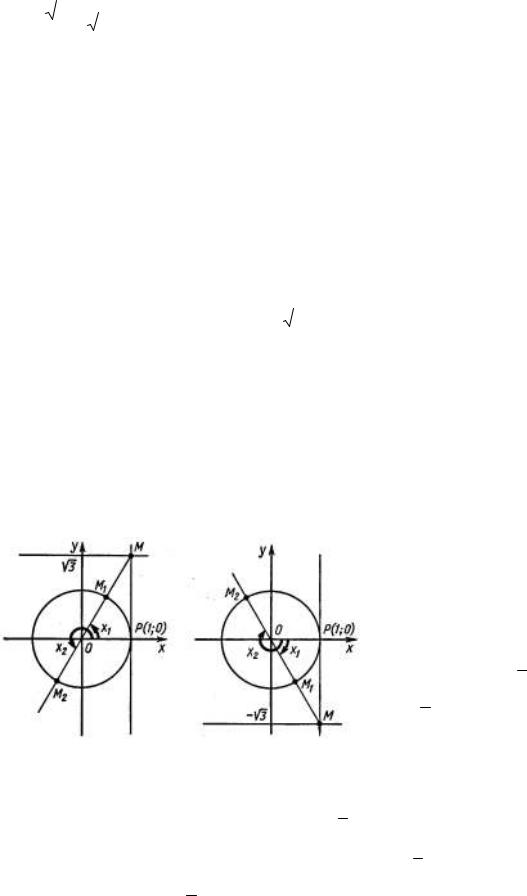
Рисунок 4.3. Тригонометрическая окружность с отмеченными на ней углами, тангенсы которых равны 
 3 (слева)
3 (слева)
и − 
 3 (справа)
3 (справа)
Задача 2. Решить уравнение tgx = −
 3 .
3 .
Решение. Углы, тангенсы которых равны (− 
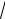 3 ), указаны на рисунке 4.3, где PM PO, PM =
3 ), указаны на рисунке 4.3, где PM PO, PM = 
 3 . Из прямоугольного треугольника РОМ находим
3 . Из прямоугольного треугольника РОМ находим

29
POM = |
π , т.е. x |
1 |
= −π . Таким образом, точка M |
1 |
получается из точки P(1;0) |
|||
|
3 |
3 |
|
|
|
|
||
|
|
|
|
|
|
|
||
поворотом вокруг |
начала |
координат |
на угол |
|
− π , а также на углы |
|||
|
|
|
|
|
|
|
|
3 |
x = −π + 2πk , где k Z. |
Точка M |
2 |
получается поворотом точки P(1;0) на |
|||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
углы x = −π + π (2k +1), где k Z. Поэтому корни уравнения tgx = −
 3 можно
3 можно
3
найти по формуле x = −π + πn, n Z.
3
Ответ. x = −π + πn, n Z.
3
Итак, каждое из уравнений tgx = 
 3 и tgx = −
3 и tgx = −
 3 имеет бесконечное
3 имеет бесконечное
множество корней. На интервале − π < x < π каждое из этих уравнений имеет
22
|
|
|
|
|
= π − корень уравнения |
|
|
= −π − корень |
|||||||||||
только один корень: x |
1 |
tgx = |
3 |
и x |
1 |
||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
tgx = − |
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|||
уравнения |
3 . |
|
Число |
называют |
арктангенсом |
числа |
3 |
|
и |
||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= π ; число |
− π |
|
арктангенсом числа − |
|
|
|
|
|||||||||
записывают |
arctg |
3 |
называют |
3 |
и |
||||||||||||||
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||
пишут arctg(− 
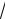 3)= −π .
3)= −π .
3
Задача 3. Решить уравнение tgx = 2.
Решение. x = arctg2 + πn, n Z.
Ответ. x = arctg2 + πn, n Z.
Задача 4. Решить уравнение (tgx + 4)(сtgx − 
 3)= 0 .
3)= 0 .
Решение. 1) tgx + 4 = 0, tgx = −4, x = arctg(− 4)+ πn, n Z.
