книги / Теория автоматического управления. Дискретные системы

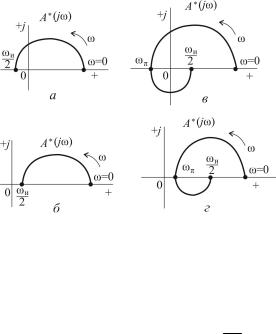
На рис. 5.3, а, в приведены примеры расположения годографа Михайлова для устойчивых систем первого и второго порядков, а на рис. 5.3, б, г – неустойчивых.

Рис. 5.3. Примеры оценки устойчивости по Михайлову

Формулировка критерия устойчивости Михайлова: «Для того чтобы замкнутая дискретная система была устойчива, необходимо

и достаточно, чтобы при изменении ω от 0 до ω2и характеристиче-

ский вектор A*(jω) имел приращение аргумента +nπ, где n – степень характеристического уравнения системы, или иначе, чтобы годограф A*(jω) обходил последовательно в положительном направлении 2n квадрантов».

5.2.2. Критерий устойчивости Найквиста

Критерий Найквиста рассматривается аналогично непрерывным системам в его обычной формулировке, причем доказательство основано, как и в 5.2.1, на использовании принципа аргумента. Так как для замкнутой системы с единичной отрицательной обрат-

81

ной связью передаточная функция имеет вид Wз (z)= W (z) , то

1+W (z)

ее полюсы определим из характеристического многочлена замкнутой системы

Приращение аргумента вектора F(z)

∆arg F(z)=∆arg Dз(z)−∆arg D(z)=nπ−(n−m)π=mπ

вдиапазоне ω от 0 до ωи / 2, где m – число полюсов разомкнутой

системы, расположенных вне единичного круга. В соответствии с этим формулировка критерия Найквиста следующая: «Для того чтобы замкнутая система была устойчива, необходимо и достаточ-

но, чтобы при изменении ω от 0 до ω2и вектор F(z), равный 1+W(z),

имел приращение аргумента mπ, где m – число корней характеристического уравнения разомкнутой дискретной системы, лежащих вне круга единичного радиуса».

Оценка устойчивости возможна при использовании как частотных характеристик разомкнутых систем, полученных в результате подстановки в передаточную функцию z=exp(jωT), т.е. W(ejωT), так и псевдочастотных характеристик W*(jλ). В последнем случае в передаточную функцию W(z) вводится заменаz=(1+jλT/2)/(1–jλT/2).

Как и для непрерывных систем, амплитудно-фазовая характеристика на комплексной плоскости, построенная в функции обычной W(ejωT) или псевдочастоты W*(jλ), не должна охватывать точку (–1, j0), или чтобы при изменении ω от 0 до ωИ/2 (λ от 0 до ∞) разность между числом положительных и отрицательных переходов АФХ разомкнутой системы через отрезок (–∞, –1) действительной оси была равна нулю, если в разомкнутом состоянии система устойчива или нейтрально-устойчива.

82

Устойчивость разомкнутой дискретной системы определяется устойчивостью ее непрерывной части, так как полюсы передаточной функции разомкнутой системы совпадают с полюсами передаточной функции непрерывной части.

Так как построение АФЧХ разомкнутой системы на комплексной плоскости оказывается громоздким для систем выше 2-го порядка, критерий Найквиста особенно удобно использовать по логарифмическим псевдочастотным характеристикам, с формулировкой, совпадающей с критерием для непрерывных систем. В этом случае удобно пользоваться понятиями запасов устойчивости ввиду простоты их определения.

5.3. Исследование качества дискретных систем

Качество дискретных систем характеризуется такими же показателями, как и качество непрерывных систем: точностью в установившемся режиме, показателями переходных режимов.

5.3.1. Точность в установившемся режиме

Оценка точности в установившемся режиме цифровых систем производится по величине установившейся ошибки при различных типовых воздействиях, наиболее характерных для исследуемой системы.

В замкнутой ЦАС со структурной схемой на рис. 3.7 рассогласование e[n], задающее r[n] и возмущающее f[n] воздействия связаны следующим уравнением относительно z-изображений:

Выражение (5.8) содержит две составляющие ошибки, первая из которых Er (z) обусловлена задающим воздействием, а вторая E f (z) – возмущающим.

83

Установившаяся ошибка цифровой системы может быть вычислена по выражению, определяющему конечное значение оригинала, т.е.

В статическом режиме работы системы на вход подается по-

иназывается ошибкой системы по скорости;

•если входной сигнал изменяется с постоянным ускорением,

т.е. r[n] = R2 (nT )2 , то z-изображение имеет вид

2

84

называется ошибкой системы по ускорению.

Рассмотренный способ определения установившейся ошибки системы удобен только при типовых входных воздействиях. Если функция r(t) имеет произвольную форму, достаточно плавную вдали от начальной точки, т.е. имеет там конечное число производных, не равных нулю, то для вычисления ошибки можно воспользоваться понятием коэффициентов ошибок. Разложив передаточную

функцию замкнутой системы по сигналу ошибки Wзε(z)для задающего воздействия в степенной ряд по (1 – z–1), получим

где С0, C1, C2, …, Cm,… называют коэффициентами ошибок.

Из соотношения (5.14) следует, что для статической системы

(ν=0)

где k – передаточный коэффициент разомкнутой системы.

Длясистемысастатизмомпервогопорядка(ν =1, С0 = 0) имеем

где kν – добротность системы по скорости.

85

Для системы с астатизмом второго порядка С0 =C1=0, поэтому из (5.13) следует

где kε – добротность системы по ускорению.

Аналогичным образом могут быть найдены и другие коэффициенты ошибок Cm.

По коэффициентам ошибок можно построить ряд, представляющий решетчатую функцию ε [nT], начиная с некоторого момента t=kT после начала переходного процесса. Такой ряд имеет вид

Применимость рассмотренного способа расчета установившейся ошибки зависит от скорости сходимости ряда (5.15).

5.3.2.Методы оценки качества переходных режимов

Вдискретных системах управления выходной сигнал обычно является функцией непрерывной переменной t объекта управления. Поэтому основные показатели качества переходных процессов, используемые для непрерывных систем, для дискретных систем определяются обычным способом.

Оценку таких качественных показателей, как быстродействие

изапас устойчивости, можно делать, используя обычные методы по переходным характеристикам. Если для анализа дискретных систем используется Z-преобразование, переходные режимы описываются решетчатыми функциями. Дискретное представление переменных в таких случаях может дать ошибочный результат при наличии в системе запаздывания или неправильном выборе частоты квантования непрерывного сигнала.

86

Аналогично непрерывным системам анализ показателей качества переходных режимов может проводиться прямыми и косвенными методами.

Показатели качества переходных режимов прямыми методами определяются по z-изображениям решетчатой функции, описанными в подразд. 2.4, в результате:

•обратного преобразования Лапласа;

•применения формул разложения;

•разложения в степенной ряд;

•разложения на простые дроби.

Эффективным прямым методом является анализ качества по результатам имитационного моделирования дискретных систем.

Из косвенных можно отметить оценку качества по расположению корней характеристического уравнения, использование частотных характеристик разомкнутых или замкнутых систем.

5.3.3. Корневые методы оценки качества переходных процессов

На рис. 5.1 показана связь расположения корней характеристичеcкого уравнения системы 2-го порядка на р- и z-плоскостях и соответствующие им переходные процессы. Как известно, для непрерывных систем комплексно-сопряженные корни, расположенные в левой полуплоскости корней, обусловливают экспоненциально затухающие синусоидальные процессы. Такие же корни дискретных систем, расположенные в левой полуполосе р-плоскости, и соответствующие им корни на z-плоскости внутри единичного круга определяют дискретно затухающий периодический процесс. Чем ближе эти комплексные корни к единичной окружности, тем более колебательным является переходный процесс.

Корни, расположенные на единичной окружности z-плоскос- ти, эквивалентны полюсам, расположенным на мнимой оси основной полосы p-плоскости. Это означает, что система находится на границе устойчивости и в ней возникают незатухающие колебания с частотой, равной значению полюса.

87

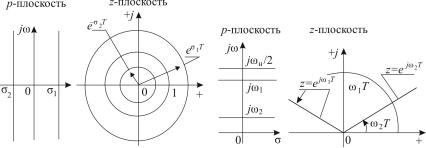
Расходящиеся переходные процессы соответствуют комплексным корням, расположенным вне единичного круга z-плоскости. Указанные соображения для систем второго порядка сохранят силу и для систем более высокого порядка, доминирующие полюсы которых позволяют свести их к системам второго порядка.

Рассмотрим отображение основных показателей переходных режимов на z-плоскости. Все точки левой р-полуплоскости отображаются в одном и том же единичном круге z-плоскости, поскольку для целых значений n имеем

ского процесса. Линии постоянного затухания (σ=const) отображаются на z-плоскости в окружности, как показано на рис. 5.4, с радиусом z=eσT и с центром в начале координат.

Линии постоянной частоты (ω=const) отображаются на той же плоскости в лучи, исходящие из начала координат под углом θ=ωT

(рис. 5.5).

Линии, соответствующие постоянному коэффициенту затухания β на р-плоскости, описываются соотношением σ/ω=tgβ и показаны на рис. 5.6.

88

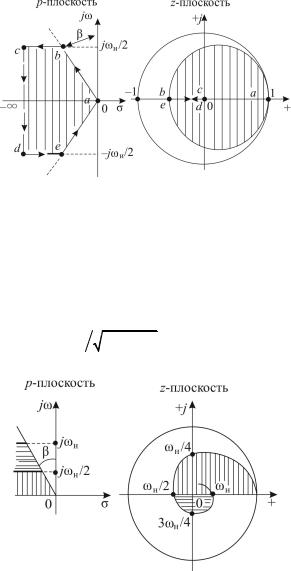
Рис. 5.6. Линии постоянного коэффициента затухания

На z-плоскости уравнение линий постоянного коэффициента затухания примет вид

Рис. 5.7. Линия постоянного значения коэффициента затухания

89

Для заданного угла β линия постоянного значения ξ, описываемая (5.17), представляет собой на z-плоскости логарифмическую спираль (кроме значений β=0 и β=90°). Заштрихованные области, показанные на p- и z-плоскостях, соответствуют друг другу (рис. 5.7). Каждые пол-оборота логарифмической спирали соответствуют отрезку линии постоянного значения ξ на p-плоскости при изменении частоты по мнимой оси на ωи/2.

Представленные на рис. 5.4–5.7 кривые равных значений показателей позволяют предсказать качество дискретных систем управления.

5.3.4. Частотные оценки качества переходных процессов

При использовании частотных методов приемы оценки качественных показателей непрерывных систем, в основном, сохраняются. Для этой цели используются как частотные передаточные функции разомкнутой системы, так и замкнутых систем. При этом могут быть определены такие критерии качества, как запасы устойчивости, показатель колебательности, полоса пропускания (частота среза) и др.

Наиболее простым и эффективным оказывается использование показателя колебательности, который определяется по АЧХ замкнутой системы M = Aз*.макс (ω)/ Aз* (0). Значение М можно находить с помощью номограмм равного значения M=const, полученных для непрерывных систем. При этом должно выполняться требование, чтобы АФЧХ разомкнутой системы Wp* ( jω) не заходила в запрет-

ную область (круг), окружающую точку (–1, j0), как показано на рис. 5.8. Радиус этой окружности R=M/(M 2–1), а ее центр сдвинут влево от начала координат на величину C=M 2/(M 2–1).

Для того чтобы дискретная система была «качественной», например, чтобы перерегулирование составляло 0,15–0,3, достаточно, чтобы значение колебательности было в пределах 1,2–1,5, значения запасов устойчивости соответственно – 8–12 дБ и 30–50°.

90