
книги / Теория автоматического управления. Дискретные системы
.pdfпричем степень числителя не выше степени знаменателя, полюса F(z) простые, тогда
l |
A0 (zv ) |
|
z |
|
F (z)=∑ |
|
|
|
, |
B' (zv ) |
|
z −zv |
||
v=1 |
|
|
где B'(z) – производная знаменателя по z; zν – корни знаменателя.
Слагаемому z/(z–zν) соответствует оригинал exp(–ανnT)=zνn, где
αν= T–1ln zν–1.
Оригинал изображения (решетчатая функция) будет
l |
A |
(z |
v |
) |
|
f [n]=∑ |
0 |
|
|
zvn . |
|
B' (z |
|
) |
|||
= |
v |
|
|||
v 1 |
|
|
|
|
|
Если числитель изображения не имеет нулевого корня и степень числителя меньше степени знаменателя, начальное значение решетчатой функции f[0]=0. После умножения числителя и знаменателя на z изображение примет вид
|
A(z) |
|
1 |
l |
A(zv ) z |
|
|||
F (z)= |
|
= |
|
∑ |
|
|
|
. |
|
B(z) |
z |
B' (zv ) z −zv |
|||||||
|
|
v=1 |
|
||||||
Множитель 1/z перед суммой означает запаздывание в решетчатой функции на один такт. Поэтому в решетчатой функции следует сделать замену n на (n–1):
l |
A |
(z |
v |
) |
|
|
f [n]=∑ |
0 |
|
|
zvn−1 |
, |
|
B' (z |
|
) |
||||
= |
v |
|
|
|||
v 1 |
|
|
|
|
|
|
причем последнее выражение справедливо только для n ≥ 1.
3. Разложение в степенной ряд. Метод заключается в делении числителя на знаменатель дробно-рациональной функции Z-изо- бражения для разложения его в бесконечный ряд по степеням z–i (ряд Лорана). В результате получаем последовательность
F(z) = c0+c1z–1+…+ckz–k+…
31

Аналитическое выражение решетчатой функции имеет вид
∞
f [n]=∑f (nT )δ(t −nT )= f (0)δ(t)+ f (1)δ(t −T )+ f (2)δ(t −2T )+...
n=0
...+ f (k)δ(t −kT )+...
Сравнивая два ряда между собой, можно установить, что c0 = f [0], c1 = f [1], c2 = f [2], …, ck = f [k].
Пример 2.4. Для решетчатой функции, Z-преобразование кото-
рой имеет вид предыдущего примера F (z)= zbz−c , выполним раз-
ложение делением многочлена числителя на знаменатель методом «длинного» деления полиномов.
В результате имеем F(z)= b[z0+c z–1+c2z–2+ c3z–3+…], откуда решетчатая функция будет иметь вид f[n]=bcn.
4. Разложение на простые дроби. Функцию F(z) можно раз-
ложить на простые дроби так же, как и в непрерывном преобразовании Лапласа. Тогда для нахождения оригинала решетчатой функции можно воспользоваться таблицей Z-преобразований. Следует отметить одну особенность применения метода. Z-изображение решетчатых функций в числителе содержит множитель z. Поэтому на простые дроби раскладывается функция F(z)/z, а затем каждая дробь умножается на z, чтобы придать разложению надлежащую форму.
32
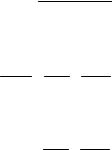
Пример 2.5. Пусть имеется изображение
F (z)= (z −(11−)(dz)−zd ),
где d=e-α, как в примере 2.2. Разложение на простые дроби дает
F (zz) = z1−1− z −1d .
Следовательно,
F (z)= z z−1− z −z d .
Из таблицы Z-преобразований (см. табл. 2.1) найдем обратное преобразование в виде решетчатой функции, значения которой в моменты квантования определяются по формуле
f[n]= 1 – dn =1 – e–αn.
В случае, когда F(z) не содержит в числителе множителя z и не
имеет полюсов z=0, то изображение удобно представить в виде z–1zF(z)= z–1F1(z). Тогда F1(z) уже будет иметь в числителе множи-
тель z, и решение получаем разложением на простые дроби функ-
ции F1(z). Если же F(z) имеет при z=0 полюс кратности m, то изображение можно представить в виде (z–1z)m+1F(z)= z–(m+1)F1(z).
В этом случае F1(z), как и ранее, будет иметь в числителе необходимый множитель z.
Как показано выше, метод Z-преобразования является удобным средством анализа линейных дискретных систем. Однако метод имеет ограничения, которые следует учитывать при его применении.
1. Дискретное преобразование Лапласа базируется на предположении, что квантованный сигнал представляет собой последовательности импульсов, площадь которых равна амплитуде входного сигнала квантователя в дискретные моменты времени. Это предположение справедливо только в том случае, если период квантова-
33
ния намного меньше минимальной постоянной времени непрерывной части системы. Влияние данного ограничения существенно снижается правильным выбором частоты квантования.
2. В результате прямого преобразования Лапласа учитываются только значения непрерывной функции в моменты квантования. Поэтому обратное преобразование будет иметь ошибку из-за описания определяемой функции по изображениям, вычисленным в фиксированные моменты времени t=nT. Для определения значений непрерывной функции между моментами квантования используют модифицированное (смещенное) преобразование Лапласа, которое позволяет получить семейство решетчатых функций при любых значениях t. На рис. 2.3 показан принцип формирования решетчатых функций, при этом значение сдвига может изменяться в пределах 0≤ aT≤ T. Указанный способ позволяет также учесть влияние запаздывания в замкнутой дискретной системе.
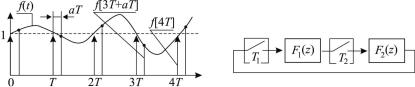
Наиболее эффективным способом снижения ошибок преобразования непрерывного сигнала является многочастотное квантование. Блок-схема простого двухчастотного преобразования приведена на рис. 2.4.
Рис. 2.3. Обычное имодифицированное |
Рис. 2.4. Блок-схема простой |
преобразование Лапласа |
многочастотной системы |
В одноконтурной системе две линейные подсистемы с периодами квантования T1 и T2, отношение которых представляет действительные числа. Работа квантователей синхронизирована, что обеспечивает возможность учета значений непрерывных функций в различные моменты времени. Данный метод достаточно просто реализуется в многопроцессорных цифровых САУ.
34
3. При анализе линейной дискретной системы методами Z-преобразования непрерывная часть должна иметь полюсов по крайней мере на один больше, чем нулей (это эквивалентно отсутствию разрыва импульсной функции для F(p) при t=0).
2.5. Соответствие между p- и z-плоскостями
Важной особенностью дискретного сигнала является его периодичность, которая определяется периодом квантования непрерывного сигнала (частотой следования импульсов) ωи=2π/T:
e− j(ω+rωи)nT =e− jωnT e− jrn2π =e− jωnT .
Спектры дискретных сигналов, таким образом, можно рассматривать в диапазоне частот –ωи/2<ω≤ +ωи/2; для других частот картина будет периодически повторяться.
Изображение F*(p) также периодично на комплексной плоскости p вдоль мнимой оси с периодом ωи, поэтому его полюсы рассматриваются в ограниченной полосе, называемой основной. На комплексной z-плоскости полосы частот (основная и дополнительные) отображаются внутри единичного круга с центром в начале координат, причем точки левой половины основной полосы располагаются внутри круга. Точки правой половины p-плоскости отображаются на z-плоскости вне единичного круга. Полюсы F(z), соответствующие полюсам F*(p), располагающимся на участках мнимой оси основной и дополнительных полос p-плоскости, лежат на окружности.
На рис. 2.5 приведено расположение полюсов изображений непрерывных и дискретных функций в основной и дополнительной полосах комплексной плоскости p, на рис. 2.6 – на плоскости z.
35
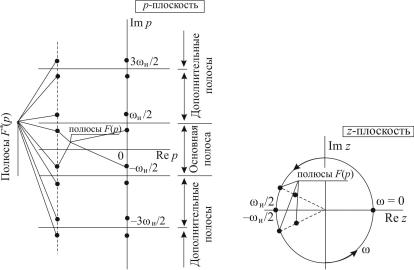
Рис. 2.5. Полюсы F(p)и F*(p) |
Рис. 2.6. Расположение полюсов |
на комплексной p-плоскости |
F(p) на z-плоскости |
Инженерные методы проектирования непрерывных систем управления основаны на анализе распределения полюсов передаточной функции на p-плоскости. Аналогично полюсы и нули Z-пре- образования передаточной функции определяют реакцию дискретной системы в моменты замыкания.
36
3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДИСКРЕТНЫХ СИСТЕМ УПРАВЛЕНИЯ
3.1. Передаточная функция импульсной системы
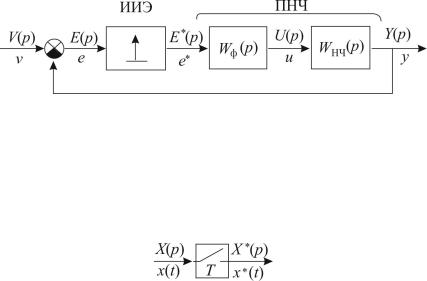
Структурная схема импульсной замкнутой системы, соответствующая типовой функциональной схеме с учетом описанных в подразд. 1.2 ее элементов, имеет вид, приведенный на рис. 3.1.
Рис. 3.1. Структурная схема замкнутой импульсной системы
На структурных схемах дискретных систем принято обозначение идеального импульсного элемента (ИИЭ) в виде ключа с периодом замыкания Т, как показано ниже, у которого на входе – непрерывный сигнал x(t), на выходе – импульсная функция x*(t), равная сумме модулированных и смещенных единичных импульсов:
Полученная в подразд. 1.2 передаточная функция формирователя прямоугольных импульсов (экстраполятора нулевого порядка) при длительности импульсов, равных периоду квантования, и действии на входе идеального единичного импульса будет совместно с непрерывной частью иметь вид
W |
(p)= |
1−e−Tp |
W |
(p), |
(3.1) |
|
|||||
ПНЧ |
|
p |
НЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |
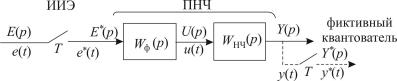
обозначается она как передаточная функция приведенной непрерывной части.
Структурная схема импульсной системы в разомкнутом состоянии с учетом этого будет иметь вид, приведенный на рис. 3.2.
Рис. 3.2. Структурная схема разомкнутой импульсной системы
Связь вход–выход приведенной части системы описывается
как
Y(p) = WПНЧ(p)E*(p). |
(3.2) |
Уравнение (3.2) невозможно описать обыкновенной передаточной функцией, поэтому для упрощения описания системы выходной непрерывный сигнал рассматривается в дискретные моменты времени, совпадающие с моментами замыкания идеального импульсного элемента на входе. Это равносильно тому, что в системе имеется фиктивный квантователь, синхронизированный с входным квантователем, и непрерывная выходная функция представляется импульсной решетчатой y*(t).
В этом случае можно получить отношение дискретных изображений выходного и входного сигналов в виде дискретной передаточной функции преобразованной разомкнутой импульсной системы:
Y*(p) = W*ПНЧ(p)E*(p), |
(3.3) |
и передаточную функцию в форме Z-преобразования:
Y(z) = WПНЧ(z)E(z). |
(3.4) |
38

Передаточная функция разомкнутой импульсной |
системы |
с типовой структурой определяется в результате D- или Z-преобра- |
|
зования Лапласа приведенной непрерывной части: |
|
Wр*(р)=D{WПНЧ(р)} или Wр(z)=Z{ WПНЧ(р)}. |
(3.5) |
Рассмотрим порядок определения импульсной передаточной функции для различных структур разомкнутых систем, показанных на рис. 3.3.
Рис. 3.3. Некоторые структуры дискретных систем
Пусть в структуре разомкнутой системы имеются две последовательно соединенные непрерывные части с экстраполяторами (см. рис. 3.3, а). Если квантователи синхронизированы, то для второй части системы можно записать
Y(p)=W2(p)U*(p) и Y(z)= W2(z)U(z). |
(3.6) |
Для первой части аналогично имеем |
|
U(p)= W1(p)X*(p) и U(z)= W1(z)X(z). |
(3.7) |
39
Решая совместно (3.6) и (3.7) получим общую передаточную функцию разомкнутой системы в виде произведения передаточных функций:
Y(z)= W1(z)W2(z)X(z). |
(3.8) |
Если в системе имеются два непрерывных звена, не разделенные квантователем (см. рис. 3.3, б), передаточная функция разомкнутой системы примет вид
Y(p)=W1(p)W2(p)X*(p), Y(z)=Z{W1(p)W2(p)}X(z),
W(z)=Z{W1(p)W2(p)} =W1W2(z)= W2W1(z). |
(3.9) |
Из полученного выражения следует, что перед применением z-преобразования следует перемножить непрерывные передаточные функции звеньев.
Если квантователь расположен между двумя непрерывными звеньями (см. рис. 3.3, в), тогда уравнение разомкнутой системы имеет вид
Y(p)=W2(p)U*(p)= W2(p) W1X*(p) и Y(z)= W2(z) W1X(z). (3.10)
В данном случае передаточной функции не существует, так как X(z) нельзя выделить из W1X(z). Это значит, что если входной сигнал не квантован, выходной сигнал y(t) должен зависеть от входного x(t) во все моменты времени, а не только в моменты квантования. Однако X(z) не содержит информации о входном сигнале в промежутках между моментами квантования.
3.2. Передаточные функции цифровых систем
Цифровые системы управления различаются способом включения цифрового регулятора в структурную схему. Принято называть системы управления цифроаналоговыми, имеющими структурную схему, соответствующую приведенным функциональным схемам на рис. 1.5 с непрерывным или цифровым задающим сигналом. В них непрерывные звенья присутствуют только на выходе
40
