SCT_1_1

Наиболее общей формой уравнения, решаемого в задачах электродинамического моделирования методом моментов, является так называемой интегральное уравнение электрического поля (electric field integral equation, EFIE). Оно может быть записано в следующем обобщенном виде

электрического и магнитного токов соответственно. Как правило, программы, реализующие EFIE, используются для моделирования задач с открытыми границами (неограниченными), в которых электрическое поле доминирует в ближней зоне источника.

Другое уравнение, решаемое методом моментов, – интегральное уравнение магнитного поля (magnetic field integral equation, MFIE),

записываемое в общем виде как

где Hinc – напряженность стороннего магнитного поля. Метод MFIE подходит главным образом для решения задач с циркулирующими токами, где доминирующим является магнитное поле.

Формулировки метода моментов, основанные только на EFIE или только на MFIE, могут обладать нестабильным поведением, когда моделируемые поверхности образуют резонатор на определенной частоте. Решение, позволяющее избежать возникновения ошибок, заключается в создании интегрального уравнения комбинированного поля (combined field integral equation, CFIE), устойчивость которого была численно доказана для любого вида резонансных эффектов.

Формулировка CFIE требует большего объема вычислений для заполнения матрицы системы, но позволяет получить более стабильное решение, когда моделируемая поверхность достаточно велика для поддержания внутренних резонансов. Для трехмерных проводящих объектов CFIE представляет собой линейную комбинацию EFIE и MFIE в

где W – собственный импеданс окружающей среды. Параметр α изменяется в пределах от 0 до 1 и может иметь любое значение из этого промежутка. Считается, что α = 0.2 является оптимальной величиной.

MLFMM используется для решения дискретизации метода моментов CFIE на поверхностной сетке разбиения (см. рис. 2.16). Поэтому, в отличие от стандартных методик MoM, решающее устройство, основанное на методе интегральных уравнений с MLFMM, снижает полный набор связей до одной в пределах многочисленных кубических областей модели. Последние затем

71

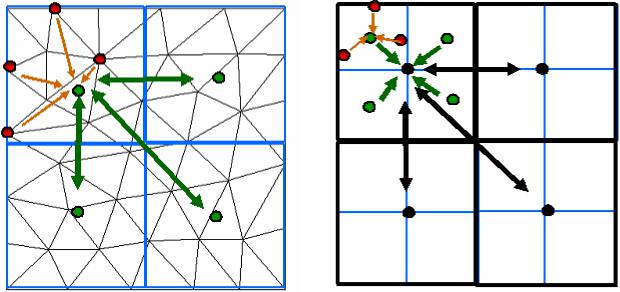
схожим образом рекурсивно объединяются в большие области, пока не получится одна область. При этом масштабирование по числу элементов разбиения значительно улучшается до Nlog(N).

Для применения метода моментов к CFIE неизвестное распределение тока J(R) раскладывается при помощи соответствующего набора из N базисных функций в ряд в соответствии со стандартной дискретизацией по Галеркину. В результате получается система линейных алгебраических уравнений, которая может быть записана в виде

i=1

Элементы матрицы А определяются как скалярное произведение выбранных базовых функций и интегрального оператора из CFIE. Следовательно, применение MoM аппроксимирует интегральные уравнения матричными. Эти линейные уравнения могут быть эффективно определены с помощью быстрого мультипольного метода (fast multipole method, FMM) [8], использующего разделение членов, отражающее связи от ближайших областей, так что соответствующая левая часть (2.51) может быть записана в матричном виде

где Anear характеризует ближнее взаимодействие элемента с элементом, а Afar

– дальнее взаимодействие группы элементов с группой (см. рис. 2.17).

Рис. 2.17. Иллюстрация взаимодействий между блоками в иерархиях FMM (а)

и MLFMM (б)

72

MLFMM является рекурсивным расширением FMM, где векторное матричное умножение реализуется в иерархической или многоуровневой многоступенчатой форме, которая может быть представлена в виде

i=1

где Vi, Ti и Ui представляют собой матрицы агрегации, переноса и дезагрегации соответственно, на i-м уровне, NL - общее число уровней. Эти

матрицы, также как и Anear , являются разреженными. В MLFMM Vi и Ui (i < NL) вычисляются путем методов интерполяции и сопряженных с ними методов антерполяции (anterpolation). Для N неизвестных порядки вычислительной сложности в памяти и времени анализа составляют Nlog(N).

В заключение отметим, что решающее устройство I-solver, основанное на методе интегральных уравнений, является специализированным решающим устройством, реализующим MLFMM, и предназначено для расчета структур больших электрических размеров. Поэтому оно хорошо подходит для решения большемерных задач.

73