
- •Методические указания
- •Для подготовки к Госэкзамену
- •Тема Кодирование информации
- •Помехозащищенные коды.
- •Экономичные коды.
- •Вероятность ошибочного приема кода
- •Примеры решения задач
- •Тема Преобразование информации Первичные преобразователи
- •Квантование сигналов
- •Примеры решения задач
- •Тема Передача информации по каналам связи. Физический уровень.
- •Логический уровень.
- •Конкретные типы дискретных каналов.
- •Примеры решения задач
- •Тема Конечные автоматы
- •Примеры решения задач
- •Тема Дискретные цепи Маркова
- •Примеры решения задач
- •Тема Системы массового обслуживания Одноканальная смо с очередью
- •Многоканальная смо без очереди
- •Многоканальная смо с очередью.
- •Примеры решения задач
- •Тема Моделирование случайных факторов Моделирование непрерывных случайных величин
- •Моделирование потоков событий
- •Примеры решения задач
Примеры решения задач
Задача 12.
По заданным таблицам переходов и выходов для конечного автомата с тремя состояниями, двумя входными и двумя выходными сигналами построить граф автомата и матрицы переходов и выходов. Определить к какому классу относится данный автомат.
Таблица переходов Таблица выходов.
x z z0 z1 z2 x1 y1 y1 y2 x2 y1 y2 y1
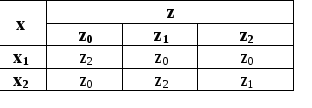
Решение
Граф автомата, заданного исходными таблицами:

Матрицы переходов и выходов:
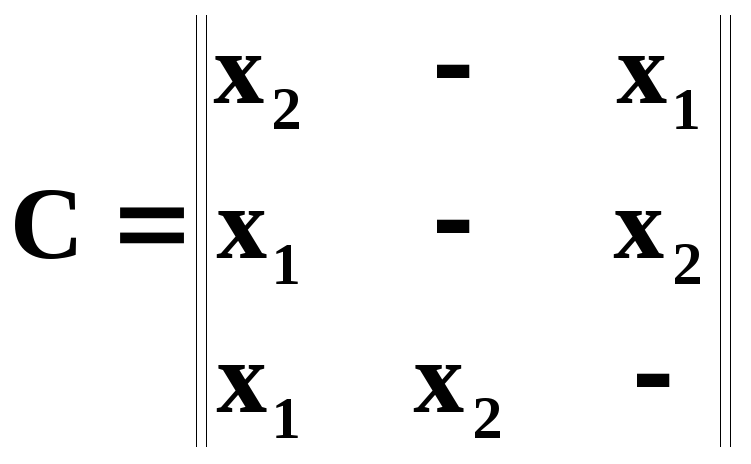
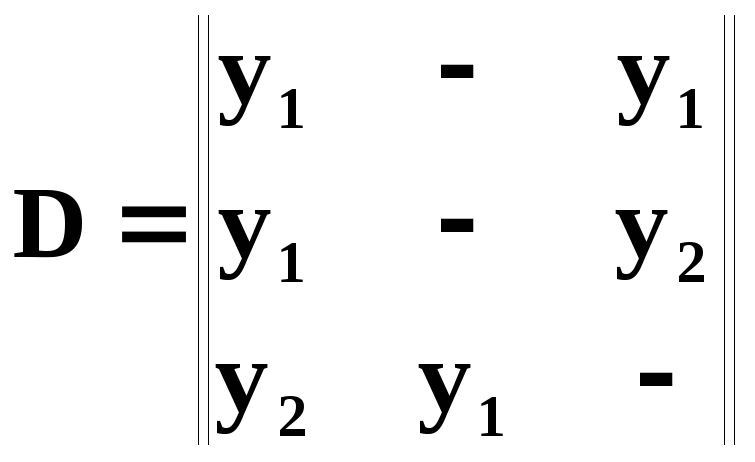
Поскольку, как состояние автомата, так и его выходной сигнал зависят от входного сигнала и предыдущего состояния, рассматриваемый автомат относится к классу автоматов Мили.
Тема Дискретные цепи Маркова
Случайный процесс, протекающий в системе A, называется марковским или случайным процессом без последствия, если для любого момента времениt0вероятность любого состояния системы приt > t0зависит только от ее состояния приt = t0и не зависит от того, как и когда система пришла в это состояние. Если число состояний Ai, которые система может принимать, конечно, то такие системы описывает марковский случайный процесс с дискретными состояниями, или марковская цепь.
Если переходы системы из одного состояния в другое возможны в строго определенные, заранее фиксированные моменты времени tj, то такую систему описывает марковский случайный процесс с дискретным временем. Марковский случайный процесс с дискретными состояниями и дискретным временем называют дискретной марковской цепью.
Обычно марковскую цепь изображают в виде графа, вершины которого соответствуют возможным состояниям системы Ai, а дуги - возможным переходам системы из состояния Ai Aj. Каждой дуге соответствует переходная вероятностьpij(k)=p[Aj(k)/Ai(k-1)]- это условная вероятность перехода системы наk-ом шаге в состояние Ajпри условии, что на предыдущем(k-1)-ом шаге система находилась в состоянии Ai.
Полным описанием марковской цепи служат матрицы переходных вероятностей:
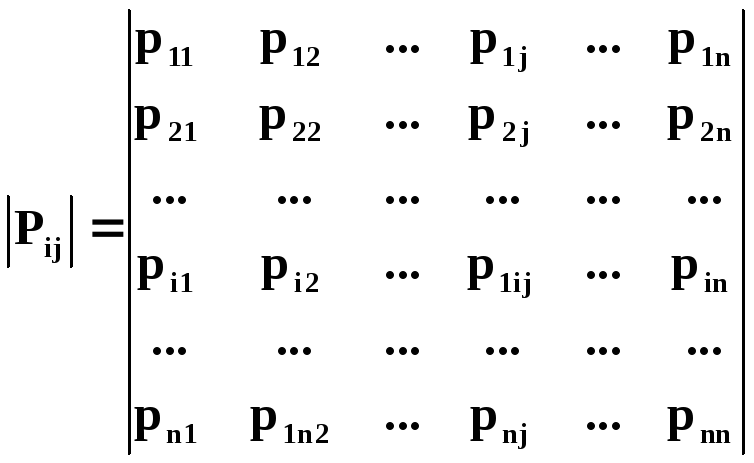
![]()
![]()
Кроме того, на каждом шаге Марковская цепь характеризуется вектором вероятностей состояний:
S(t) = [S1(t),S2(t),. . . Sn(t)]
Вероятностью i-го состояния называется вероятностьSi(t)того, что в моментtсистема будет находиться в состоянииAi.Очевидно, что для любого моментаtсумма вероятностей всех состояний равна единице:
![]()
Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага. Если переходные вероятности меняются от шага к шагу, марковская цепь называется неоднородной.
Все многообразие Марковских цепей подразделяется на эргодическиеиразложимые.
Эргодические Марковские цепи описываются сильно связанным графом. Это означает, что в такой системе возможен переход из любого состояния Aiв любое состояниеAj(i = 1..n) за конечное число шагов.
Эргодическая цепь Маркова обладает очень важным свойством. При неограниченном увеличении числа шагов (tстремится к бесконечности) вероятности состояний системы[S(t)]стремятся к предельным значениям и перестают изменяться, т.е. зависеть от времени. Система приходит к стационарному режиму, при котором[S]= const.
Очень важным является то обстоятельство, что значения предельных вероятностей состояний не зависят от распределения вероятностей в начальный момент времени. То есть система может прийти к одному и тому же стационарному распределению вероятностей из любого исходного состояния.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состояния равна 0,5, то это означает, что в среднем половину времени система находится в этом состоянии.
Для определения предельных вероятностей состояний следует решить систему линейных уравнений:
![]() j
= 1, …n
j
= 1, …n
Можно показать, что система (5.8) является линейно зависимой, поэтому для ее решения необходимо заменить любое из уравнений условием нормировки вероятностей
![]()
Составить приведенную выше систему линейных уравнений довольно просто, используя граф цепи Маркова. В левой части каждого уравнения стоит вероятность рассматриваемого состояния, а в правой части - столько слагаемых, сколько дуг графа входит в рассматриваемое состояние. Каждое слагаемое равно произведению вероятности перехода, соответствующей данной дуге графа, на вероятность того состояния, из которого исходит дуга графа
