
книги / Прикладной статистический анализ в горном деле (Одномерная математическая статистика и регрессионный анализ)
..pdfся потому, что каждый из факторов действует случайно. Их нельзя устранить, но можно уменьшить влияние, увеличивая число измерений.
Грубые погрешности измерений (выбросы) могут сильно исказить среднее, дисперсию и другие статистические оценки, поэтому их исключают из серии измерений. Обычно в ряду полученных результатов они сразу видны, тем не менее в каждом конкретном случае необходимо доказать наличие выбросов. Существует ряд критериев для фиксирования выбросов. Например, критерий 3 служит для выявления и исключения грубых погрешностей. Применяется этот критерий, если выборка результатов измерений подчинятся нормальному закону распределения и количество данных более 30–50. В геодезии теодолитные и нивелирные ходы имеют ограничения по длине или по количеству штативов, поэтому и количество данных невелико. И тогда критерий может быть уменьшен до 2 [47].
Любая выборка дает лишь приближенное представление о генеральной совокупности, и все выборочные статистические характеристики (средняя, дисперсия и др.) являются некоторым приближением, или оценкой генеральных параметров. Эти оценки ещё именуют точечными, потому что для замены неизвестного параметра предлагается конкретное число. Положительная сторона точечной оценки в том, что это однозначное число (или несколько чисел – оценок параметров) можно поставить в формулу распределения и тем самым полностью восстановить закон распределения вероятностей анализируемых данных. К сожалению, точечные оценки параметров не дают представление о степени их точности (насколько эти оценки будут отличаться от параметров генеральной совокупности) и о надежности полученной оценки. Особенно часто вопрос о точности и надежности оценки возникает тогда, когда объем выборки недостаточно велик. Параметры генеральной совокупности (математическое ожидание, среднее квадратическое отклонение и др.) вычислить в большинстве случаев не представляется возможным, по меньшей мере по двум
131
причинам. Первая из них – недоступность всех объектов генеральной совокупности, а вторая – наличие погрешностей измерений. В этом случае принято указывать интервал, в котором с определенной долей вероятности лежит истинное (генеральное) значение статистической характеристики. Этот интервал называется доверительным интервалом (ДИ) и уже упоминался ранее.
4.3. Точечные оценки и требования к ним
Ранее рассматривались некоторые оценки выборки: среднее значение, дисперсия, стандартное отклонение и др. Выбор той или иной меры для оценки параметров генеральной совокупности связан со свойствами оценок. Любые характеристики распределения вероятностей могут быть выражены через его параметры. Поэтому одна из основных задач статистики заключается в том, чтобы по выборочной совокупности случайной величины сделать выводы о параметрах распределения, вычислить их приближенные значения. В геодезии, маркшейдерии, горном деле и во многих других отраслях промышленности чаще всего используется нормальный закон распределения вероятностей. Его параметрами являются математическое ожидание и дисперсия. Другие законы распределения могут иметь иные параметры.
Введем обозначения: θ – оцениваемый параметр генеральной совокупности, θn – оценка параметра θ (точечная оценка) на основе выборки объема n. Сделав допущение о типе закона распределения, мы по выборке получаем приближенные значения (точечные оценки) его параметров. Оценка – это функция от нашей выборки. Но таких функций от выборки можно придумать великое множество. Очевидно, что эта оценка должна удовлетворять нескольким условиям, по меньшей мере она не должна значимо отличаться от оцениваемого параметра генеральной совокупности. Под «хорошей» понимают такую оценку θn, которая с большой вероятностью близка
132

к истинному параметру θ. Рассмотрим желательные свойства точечной оценки.
1. Состоятельность. Оценка θn называется состоятельной, если при неограниченном росте объема выборки (n → ∞) эта оценка стремится к неизвестному истинному значению параметра (θn → θ). В математической статистике доказано, что состоятельной оценкой генерального среднего значения μ явля-
ется выборочное среднее арифметическое xв , а состоятельной оценкой генеральной дисперсии σ2 – выборочная дисперсия σ2в. Методы вычисления этих выборочных характеристик были рассмотрены ранее.
2. Несмещенность. Оценка θn называется несмещенной, если ее математическое ожидание совпадает с неизвестным истинным значением параметра, т.е. M (θn) = θ, или, иными словами, если она не содержит систематической составляющей. Таким образом, несмещенная оценка оказывается истинной в среднем. Более слабым условием является асимптотическая несмещенность, которая означает, что математическое ожидание оценки сходится к истинному значению параметра с ростом объема выборки. Выборочное среднее арифметическое хв является несмещенной оценкой генерального среднего μ.
Одним из свойств выборочного среднего арифметического является положение о том, что сумма квадратов отклонений значений признака от среднего арифметического меньше, чем сумма квадратов отклонений от любой другой величины (в том числе и от генерального среднего μ). В случаях, когда анализируемые данные содержат систематическую составляющую, то и вычисленные оценки дисперсии по формуле (4.1) будут содержать систематическую ошибку и такая оценка будет смещенной.
n xi x 2
2 |
i 1 |
|
. |
(4.1) |
|
n |
133

Несмещенной оценкой генеральной дисперсии σ2 является исправленная выборочная дисперсия, вычисляемая по формуле (4.2), поскольку при неограниченном повторении выборки из генеральной совокупности и усреднении выборочной дисперсии, полученной на основании этой формулы, по всем выборкам получается истинное значение генеральной дисперсии.
n xi x 2
S 2 |
i 1 |
|
. |
(4.2) |
|
n 1 |
|||
|
|
|
|
Однако нам недостаточно иметь «истинное» в среднем значение, хотелось бы еще, чтобы разброс значений вблизи этого среднего был как можно меньше. Степень разброса выборочной оценки вблизи истинного значения как раз и характеризует следующее свойство оценок, называемое эффективностью.
3. Эффективность. Несмещенная оценка θn называется эффективной, если она имеет минимально возможную дисперсию в классе всех несмещенных оценок. Это надо понимать так: полученные по выборке оценки хв и S 2 – случайные величины, так как случайны сами выборочные значения. Поэтому принято говорить о математическом ожидании и дисперсии оценок хв и S 2. Эффективность этих оценок означает, что их дисперсии D (хв) и D (S 2) меньше дисперсий любых других несмещенных оценок среднего значения и дисперсии генеральной совокупности.
Итак, наилучшими в указанном смысле оценками генерального среднего значения и генеральной дисперсии являются выборочные характеристики хв и S 2. Численное значение эффективности оценки можно определить отношением минимально возможнойдисперсиикдисперсииданнойнесмещеннойоценки.Таким образом, эффективность есть число в интервале от нуля до единицы,причемэффективностьнаилучшейоценкиравнаединице.
4. Робастность. Оценка θn называется робастной, если она устойчива к резко выделяющимся наблюдениям.
134
Из рассмотренных требований только состоятельность является практически обязательным требованием к статистическим оценкам, остальные представленные выше свойства являются скорее пожеланиями, чем обязательными требованиями, чаще всего все требования не могут быть удовлетворены одновременно. В ряде случаев при отборе проб, при выполнении химических анализов, при измерениях и их обработке имеются соответствующие методики проведения работ, направленные на уменьшение или даже на исключение грубых и систематических погрешностей в конечных данных. Например, коллимационная ошибка (систематическая составляющая) теодолита будет исключена при измерении углов методом приёмов (двумя полуприёмами: один при круге лево, второй – при круге право). Измерения длин сторон теодолитного хода рулеткой выполняется несколько раз, грубые измерения не принимаются в расчёт. На величину погрешности имеются ограничения, прописанные в методиках работы. Методическими руководствами часто рекомендуются двойные измерения. Разность между ними есть величина случайная с нулевым средним и с равномерным их рассеиванием относительно среднего. Если среднее не равно 0, имеется систематическая погрешность, и её можно устранить.
Например, рассмотрим свойства оценок параметров нормального распределения μ, σ2.
1.Оценки μ: выборочное среднее дает состоятельную, несмещенную, эффективную, но неробастную оценку. С другой стороны, выборочная медиана Me дает состоятельную, несмещенную, неэффективную, но робастную оценку. Таким образом, выборочная медиана проигрывает выборочному среднему в эффективности, но выигрывает в робастности.
2.Оценки σ2: наиболее употребительная оценка, определяемая формулой (4.3), дает состоятельную, несмещенную, эффективную, но неробастную оценку дисперсии:
135

n xi x 2
s2 |
i 1 |
|
. |
(4.3) |
|
n 1 |
|||
|
|
|
|
Заметим, что деление на (n – 1) вместо интуитивно ожидаемого n как раз и призвано обеспечить несмещенность оценки. При увеличении количества наблюдений свыше 30 можно в знаменателе выражения (4.3) использовать n. С другой стороны, оценка «сигмы» нормального распределения на основе межквартильного выборочного размаха по формуле σ = q / 1,35 дает пример неэффективной, но робастной оценки.
4.4. Стандартная ошибка среднего арифметического
Оценки xв и S 2, полученные по ограниченной выборке, не
будут совпадать с истинными значениями параметров μ и σ2 генеральной совокупности. Правда, проверить это утверждение невозможно, поскольку неизвестны истинные значения этих параметров. Но если несколько раз отбирать повторные и несовпадающие выборки из одной и той же генеральной совокупности с параметрами μ и σ2 и по каждой выборке вычислять их
оценки xв и S 2, то окажется, что эти оценки для разных выбо-
рок не будут совпадать.
Разности оценок параметров выборки от истинных значений этих параметров всей генеральной совокупности именуются статистическими ошибками, или ошибками репрезентативности. Следует понимать, что их происхождение не имеет ничего общего с ошибками измерения. Ошибки репрезентативности возникают только потому, что не все объекты генеральной совокупности представлены в выборке.
Величины статистических ошибок оценивают по среднему квадратическому (стандартному) отклонению выборочных характеристик. Здесь рассматривается только стандартное откло-
136

нение выборочного среднего арифметического. Если взять очень много независимых выборок объема k из одной и той же генеральной совокупности и определить для каждой из них среднее арифметическое, то окажется, что полученные средние арифметические варьируют вокруг своего среднего значения (равного μ) в k раз меньше, чем отдельные варианты выборки. Тогда стандартное отклонение выборочного среднего арифметического будет равно [45]
|
|
, |
(4.4) |
x n
где σ – стандартное отклонение генеральной совокупности. Когда нет параметров генеральной совокупности, в качестве оценки стандартного отклонения выборочного среднего используется величина
S |
S |
. |
(4.5) |
x n
Она именуется стандартной ошибкой среднего арифметического, или ошибкой репрезентативности. В приведенной фор-
муле S – выборочное стандартное отклонение, S S2 . Величина Sx показывает, какая ошибка в среднем допускается, если
использовать вместо генерального среднего μ его выборочную оценку хв. Поэтому вычисленное среднее арифметическое часто
указывают в виде xв x S x , чтобы оценить точность оценки х. Из формулы видно, как зависит стандартная ошибка S x от объ-
ема выборки n. С увеличением объема выборки n стандартная ошибка S x уменьшается пропорционально квадратному корню
из n. Ошибку выборочной средней иногда обозначают как mx . Границы вычисленного среднего арифметического, указываемого в виде xв x S x , могут использоваться для опреде-
137
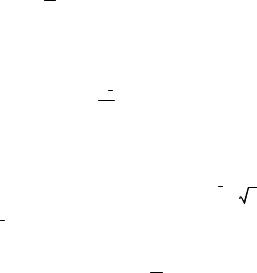
ления точности выборочной средней. Она вычисляется по формулам выборочного коэффициента вариации (формула (4.6)) в процентах как отношение ошибки репрезентативности выборочной средней к самой выборочной средней:
|
S |
|
|
|
|
|
|
Cs |
x |
100. |
(4.6) |
||||
|
|
в |
|
||||
|
|
|
|
||||
|
|
|
|||||
|
|
xв |
|
||||
Точность выборочной средней считается удовлетворительной, если коэффициент Cs 3 5%.
Теперь можно уточнить вопрос, который важен для геодезистов и горных инженеров-маркшейдеров и не был раскрыт при вычислении выборочных характеристик: с такой точностью нужно вычислять выборочные характеристики?
Как мы только что убедились, при ограниченном объеме выборки n истинное значение генерального среднего μ не может быть определено сколь угодно точно. В связи с этим и при вы-
числении xв оставлять большое число значащих цифр не имеет
смысла. Существует эмпирическое правило, согласно которому в окончательном результате положение последней значащей цифры должно соответствовать положению первой значащей
S
цифры в величине 3x [1].
Например, в таблице доверительных интервалов на
рис. 4.1 |
xв |
|
24,09931, выборочное |
|
стандартное отклонение |
||||
S = 2,350344, n = 60 (табл.4.1). Тогда S |
|
|
S |
2,350344 0,303, |
|||||
x |
|
||||||||
|
|
|
|
|
|
|
n |
7,746 |
|
|
|
|
|
|
|
|
|
||
а |
Sx |
0,101 |
. Первая значащая цифра стоит на первом месте по- |
||||||
|
|||||||||
3 |
|
|
|
|
|
|
|
|
|
сле запятой, поэтому среднее можно округлить до одного (пер-
вого) знака после запятой xв = 24,1. Вместе с тем, чтобы избежать накопления ошибок, связанных с округлением, промежу-
138

точные результаты нужно вычислять с точностью на один порядок больше, чем точность окончательных результатов. Погрешность оценки измеряемой величины следует выражать не более чем двумя значащими цифрами. По ГОСТ Р 8.736-2011 [19] две значащие цифры в погрешности оценки измеряемой величины сохраняют:
–при точных измерениях;
–еслиперваязначащаяцифраимеетзначениенеболеетрех.
4.5.Интервальные оценки
4.5.1. Общие сведения
Как указывалось ранее, выборка дает лишь приближенное представление о генеральной совокупности и все выборочные статистические характеристики являются некоторым приближением генеральных параметров.
По хлориду калия из генеральной совокупности отобрано 60 проб, их некоторые статистики приведены в табл. 4.1. Нас интересуют выборочное среднее, выборочный стандарт и экстремумы.
Таблица 4.1
Статистики по хлориду калия
Во многих исследованиях, особенно для малых выборок, требуется получить не только точечную оценку θn неизвестного параметра θ, а ещё и интервал, в котором с определенной долей вероятности лежит истинное (генеральное) значение статистической характеристики (например, p0 = 0,95 или 0,99).
139
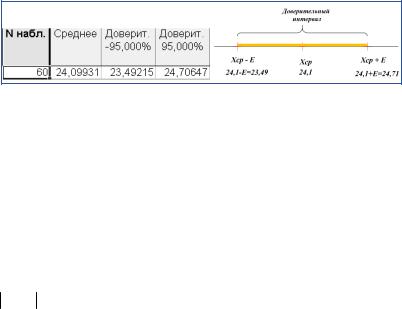
P (a < θ < b) = p0. |
(4.7) |
Используем эту формулу для записи доверительного интервала. Применительно к данным рассматриваемого примера (см. рис. 4.1) это выражение запишется следующим образом: P (23,49 < µ < 24,71) = 0,95. А интерпретируется это выражение так: с доверительной вероятностью 95 % среднее значение не будет выходить за границы доверительного интервала (в 95 случаях из 100). Доверительный интервал зависит от выборки. Поскольку выборка случайна, для каждой выборки мы будем получать свой доверительный интервал.
Например, среднее значение содержания хлористого калия по 60 пробам составляет 24,1 %. Вместе со средним значением и другими статистиками программа вычислит и доверительные интервалы. Выведем их отдельно в таблице на рис. 4.1.
а |
б |
Рис. 4.1. Доверительные интервалы: а – в таблице и б – пояснения на графике
Параметры положения и доверительные интервалы определенывпрограммеStatisticaвмодулеописательныхстатистик(рис.4.2).
Нам осталось определить величину интервала Е, представленную на правой части рис. 4.1.
Пусть найденная по результатам выборки объема n статистическая характеристика θn (x1, x2, x3, …, xn) является точечной оценкой неизвестного параметра . Чем меньше разностьn , тем лучше качество оценки, тем она точнее. Таким обра-
зом, положительное число характеризует точность оценки:
|
n |
|
. |
(4.8) |
|
|
140
