
книги / Несущая способность конструкций в условиях теплосмен
..pdf
– два кинематических условия и одно силовое условие,
ux = Ux, uy = Uy, σxz = pz;
– одно кинематическое условие и два силовых условия,
ux = Ux, σxy = py, σxz = pz;
– три силовых условия (8.1),
σxx = px, σyx = py, σzx = pz.
Записанные граничные условия дополняются начальными условиями (9.2):
u |
|
|
|
|
|
|
= U 0 |
, dux |
|
= v |
|
|
|
|
= V 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
t =0 |
x |
|
dt |
|
t=0 |
x |
|
|
t=0 |
x |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
uy |
|
|
|
|
|
= U y0 , |
duy |
|
= vy |
|
|
|
= Vy0 ; |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
t =0 |
dt |
|
|
t =0 |
||||||||||||
|
|
|
|
|
t =0 |
|
|
|
|
|||||||
u |
|
|
|
|
|
|
= U 0 |
, duz |
|
= v |
|
|
|
|
= V 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
z |
|
t =0 |
z |
|
dt |
|
t =0 |
z |
|
|
t=0 |
z |
|||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9.6. Краевые условия для двумерной задачи
При решении задач в приближении плоско-деформирован- ного, плоско-напряженного или осесимметричного состояния математическая модель содержит восемь дифференциальных уравнений в частных производных для восьми искомых функций50 σxx, σyy, σxy,
εxx, εyy, εxy, ux, uy:
ρ |
d 2u |
x |
= ρfx + |
|
∂σ |
xx |
+ |
∂σxy |
, ρ |
d |
2u |
y |
= ρf |
|
+ |
∂σ |
xy |
+ |
∂σ |
yy |
; |
|
dt2 |
|
|
∂x |
∂y |
|
|
|
y |
|
|
|
|||||||||||
|
|
dt2 |
|
∂x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂y |
|||||||||||
|
|
|
σxx = |
|
|
|
E |
|
((1 |
− ν)εxx + νε yy ); |
|
|
|
|
||||||||
|
|
|
(1+ ν)(1− 2ν) |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
50 На примере модели плоско-деформированного состояния.
101

σyy
εxx
= (1+ ν)E(1− 2ν) (νεxx + (1− ν)ε yy );
|
|
|
σxy = |
|
E |
εxy ; |
|
|
|
|
||
|
|
|
1+ ν |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
= |
∂u |
, |
ε yy = |
∂v |
, ε xy = |
1 |
|
∂u |
+ |
∂v |
||
∂x |
∂y |
2 |
|
∂y |
. |
|||||||
|
|
|
|
|
|
|
∂x |
|||||
Приведенная система уравнений может быть также преобразована к системе двух уравнений Ламе с двумя искомыми функциями
ux и uy:
ρ d 2ux dt2
ρ d 2uy dt2
=ρfx
=ρfy
+ |
|
|
E |
|
1 |
|
∂2u |
x |
+ |
∂2uy |
|
|
+ |
∂2u |
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|||||||||||
|
|
(1+ ν ) 1 |
− 2ν |
∂x2 |
|
∂x∂y |
|
∂x2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ |
|
|
E |
|
1 |
|
∂2u |
x |
+ |
∂2uy |
|
|
+ |
∂2uy |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
∂y∂x |
|
|
∂x2 |
|||||||||
|
|
(1+ ν ) 1 |
− 2ν |
|
∂y2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+∂2ux ,
∂y2
+∂2uy .
∂y2
В общем случае для каждой точки границы необходимо задавать соответственно два условия, при этом возможны следующие комбинации кинематических и силовых граничных условий:
– два кинематических условия,
ux = Ux, uy = Uy;
– одно кинематическое условие и одно силовое условие,
ux = Ux, σxy = py;
– два силовых условия,
σxx = px, σxy = py.
Записанные граничные условия дополняются начальными условиями
u |
|
|
|
= U 0 |
, dux |
|
= v |
|
|
|
= V 0 |
; |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
|
x |
|
t =0 |
x |
dt |
|
t=0 |
x |
|
t=0 |
x |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
102

uy |
|
|
= U y0 , |
duy |
|
|
= Vy0 . |
|
|
|
|
= vy |
|
||||
|
|
|
|
|||||
|
t =0 |
dt |
||||||
|
|
|
|
t =0 |
|
t =0 |
||
|
|
|
|
|
|
|
||
На рис. 9.2, а показан вариант задания граничных условий для случая осадки длинной полосы (рассматривается стационарное плос- ко-деформированное состояние) заданным усилием на шероховатых51 плитах.
На верхней границе задано граничное условие σ yy = − p , соот-
ветствующее вертикальному усилию p, направленному против оси y, и нулевое перемещение ux = 0 в направлении оси x. На нижней границе заданы условия отсутствия перемещения в направлении обеих координатных осей – ux = 0 и uy = 0 .
Вертикальные границы деформируемой полосы свободны от усилий, поэтому, согласно соотношениям Коши (8.1), на этих границах задаются условия σxx = 0 и σxy = 0.
На рис. 9.2, б представлен вариант формулировки граничных
условий для случая осадки той же полосы на заданную высоту |
на |
гладких плитах. |
|
На верхней границе задано граничное условие uy = − , |
соот- |
ветствующее заданному вертикальному перемещению верхней границы, направленному против оси y, и, согласно формуле Коши (8.1), нулевое значение компоненты тензора напряжения σ yx = 0 , соответ-
ствующее отсутствию в направлении оси x силы трения (сдвиговой нагрузки) между плитой и поверхностью деформируемого тела. На нижней границе, как и в предыдущем случае, заданы условия отсут-
ствия |
перемещения в направлении обеих координатных |
осей – |
ux = 0 |
и uy = 0 . Вертикальные границы деформируемой |
полосы |
также свободны от усилий, поэтому на этих границах задаются условия σxx = 0 и σxy = 0.
51 Плита шероховатая, если она не позволяет смещаться точкам контактной поверхности деформируемого тела. Плита гладкая, если она не препятствует смещению точек контактной поверхности деформируемого тела.
103
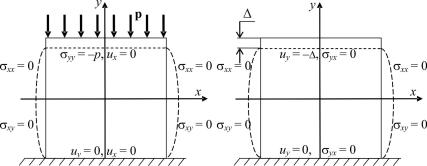
а |
б |
Рис. 9.2. Осадка длинной полосы (плоско-деформированное состояние) заданным усилием на шероховатых плитах (а) и на заданную высоту на гладких плитах (б); пунктиром обозначено деформированное состояние
9.7. Краевые условия для одномерной задачи
Для одномерных задач (растяжение, изгиб, сдвиг, кручение и проч.) система содержит три уравнения для трех искомых функций (например, σxx, εxx, ux – для одноосного растяжения):
ρ d 2ux |
= ρf |
x |
+ ∂σxx , |
|
|
σ xx = Eε xx , |
|
|
εxx = |
∂ux . |
||||
dt2 |
|
∂x |
|
|
|
|
|
|
|
|
|
|
∂x |
|
Последовательная подстановка формулы σxx = Eεxx |
закона Гу- |
|||||||||||||
ка и кинематического соотношения εxx = ∂ux / ∂x |
в уравнение дви- |
|||||||||||||
жения приводит к выражению |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
ρ |
d 2u |
x |
= ρf |
|
+ E |
∂ε |
xx |
, |
|
|
|
|
|
|
dt2 |
x |
|
|
|
|||||||
|
|
|
|
|
|
|
∂x |
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
d 2u |
x |
= ρf |
|
+ E |
∂2u |
x . |
|
(9.3) |
||
|
|
|
dt2 |
x |
|
|
|
|||||||
|
|
|
|
|
|
|
∂x2 |
|
|
|
||||
Выражение (9.3) представляет собой уравнение Ламе для случая одномерной (одноосной) деформации.
104
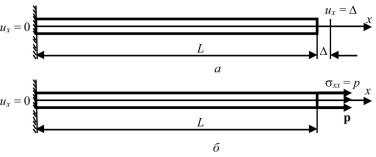
На границах задаются граничные условия:
– два кинематических условия (рис. 9.3, а),
|
|
|
|
ux |
|
|
|
|
x=0 = U0 , ux |
|
x=L = UL ; |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
– одно кинематическое |
условие |
и |
|
|
одно силовое условие |
|||||||||||||||||||||||
(рис. 9.3, б), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ux |
|
x=0 = U0 , σxx |
|
x=L = p ; |
|
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
– одно силовое условие и одно кинематическое условие, |
||||||||||||||||||||||||||||
|
|
|
σxx |
|
x=0 = − p, ux |
|
x= L = U L ; |
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
– два силовых условия, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
σxx |
|
x=0 = − p, σxx |
|
x=L = p. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
Эти условия дополняются начальными условиями |
||||||||||||||||||||||||||||
u |
x |
|
|
= U 0 , |
dux |
|
|
= v |
x |
|
|
=V 0 . |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
t =0 |
|
|
|
|
|
|
|
|
|
dt |
|
t=0 |
|
|
t=0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рис. 9.3. Деформирование призматического стержня заданным удлинением (а) и растягивающим усилием p (б)
На рис. 9.3, б показано статическое нагружение растягивающим усилием p призматического стержня, закрепленного на левом конце.
105

Для закрепленного неподвижно левого конца граничное условие имеет вид ux x=0 = 0, на правом конце задается силовое гранич-
ное условие σxx x=L = p.
Предполагая, что массовые силы f отсутствуют, деформирование стационарное, уравнение (9.3) можно упростить:
d 2u |
= 0 . |
(9.4) |
|
x |
|||
dx2 |
|||
|
|
Решение этого уравнения имеет вид ux = C1 + C2 x ,
где C1 и C2 – постоянные интегрирования. Для определения этих постоянных используются записанные граничные условия:
ux x=0 = C1 + C2 0 = 0 ;
σxx |
|
|
= E εxx |
|
|
= E |
∂ux |
|
= EC2 = p ; |
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
x=L |
|
x=L |
∂x |
|
||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
x=L |
|
|
|
|
|
|
|
|
|
C1 = 0 , C2 = Ep .
Следовательно, перемещение материальных частиц призматического стержня при растяжении усилием является линейной функцией координаты:
ux = Ep x .
Деформация и напряжение в стержне постоянны:
εxx = ∂∂uxx = Ep ;
σ xx = Eε xx = p .
106

Для схемы нагружения, приведенной на рис. 9.3, б граничное условие для закрепленного неподвижно левого конца имеет вид ux x=0 = 0, на правом конце – ux x= L = . Также с учетом предполо-
жения, что массовые силы f отсутствуют, деформирование стационарное, решение дифференциального уравнения (9.4) имеет уже известный вид
ux = C1 + C2 x .
Для определения постоянных интегрирования C1 и C2 используются граничные условия:
ux x=0 = C1 + C2 0 = 0 ; ux x=L = C1 + C2 L = ;
C1 = 0 , C2 = L .
Следовательно, перемещение материальных частиц призматического стержня при растяжении усилием является линейной функцией координаты:
ux = L x .
Деформация и напряжение в стержне постоянны:
εxx = ∂∂uxx = L ;
σxx = Eεxx = EL .
107

10. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ МЕХАНИКИ ЖИДКОСТИ И ГАЗА
Моделирование состояния элементов и узлов строительных
идорожных машин, подверженных воздействию жидкостей и газов (ветровая нагрузка, внешнее или внутреннее давление на стенки резервуаров и гидравлических цилиндров, в системах трубопроводов, вентиляционных шахтах, охлаждение и нагрев рабочих жидкостей
иэлементов радиаторных систем, управляющих механизмов, систем гидро-, пневмоавтоматики и проч.) требует корректной математической постановки (формулировки) дифференциальных уравнений механики жидкости и газа, а также соответствующих этим уравнениям краевых (граничных и начальных) условий.
Для описания механических процессов в жидкостях и газах используют:
–уравнение неразрывности (8.2)
dρ |
|
∂v |
|
∂vy |
|
∂v |
|
= 0 ; |
|
+ ρ |
|
x + |
|
+ |
|
z |
|
dt |
|
∂y |
|
|||||
|
∂x |
|
∂z |
|
||||
–уравнения движения (8.4):
ρdvx = ρf + ∂σxx + ∂σxy + ∂σxz , dt x ∂x ∂y ∂z
ρ |
dvy |
= ρfy + |
∂σyx |
+ |
|
∂σyy |
+ |
|
∂σyz |
, |
|||
dt |
|
∂y |
|
||||||||||
|
|
∂x |
|
|
∂z |
||||||||
ρ |
dv |
z |
= ρfz + |
∂σ |
zx + |
|
∂σzy |
+ |
∂σ |
zz ; |
|||
|
|
|
∂y |
|
|
||||||||
|
dt |
|
∂x |
|
|
∂z |
|||||||
–физические уравнения связи компонент тензора напряжения
скомпонентами тензора скорости деформации (7.5):
σxx = − p + λ (ξxx + ξyy + ξzz )+ 2μξxx ,
108
σyy = − p + λ (ξxx + ξ yy + ξzz )+ 2μξ yy ,
σzz = − p + λ (ξxx + ξ yy + ξzz )+ 2μξzz ,
σxy = 2μξxy , σyz = 2μξyz , σ xz = 2μξxz ;
– кинематические соотношения между компонентами вектора скорости и тензора скорости деформации (7.4):
|
|
|
|
|
ξxx = |
∂v |
x |
, |
ξyy |
= |
∂vy |
|
, ξzz = |
∂v |
z |
; |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|||||
ξ xy = |
1 |
|
∂vx |
+ |
∂vy |
, ξ yz = |
1 |
|
|
∂vy |
+ |
∂vz |
|
, |
ξxz |
= |
1 |
∂vx |
+ |
∂vz |
; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
∂y |
∂x |
2 |
|
∂z |
∂y |
2 |
∂z |
∂x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
– уравнение состояния, например закон Менделеева – Клайперона (8.6)
p = β1 ρRT ;
– уравнение теплопроводности (8.5) (для теплопроводных жидкостей и газов)
cρ |
dT |
= |
∂ |
η |
∂T |
+ |
∂ |
|
η |
∂T |
+ |
∂ |
η |
∂T |
+ q + Φ . |
||
dt |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|||||||||||||||
|
|
∂x |
|
∂x |
|
∂y |
|
∂y |
|
∂z |
|
∂z |
|
||||
Записанная система содержит семнадцать дифференциальных уравнений и одно нелинейное алгебраическое уравнение для восемнадцати искомых функций: шесть независимых компонент σxx, σyy, σzz, σxy, σyz, и σxz тензора напряжения, шесть независимых компонент ξxx, ξyy, ξzz, ξxy, ξyz, и ξxz тензора скорости деформации, три независимые компоненты vx, vy и vz вектора скорости, неизвестное давление p, неизвестную плотность ρ и неизвестную температуру T. Следовательно, количество уравнений системы соответствует количеству искомых неизвестных.
109

10.1. Уравнения движения жидкости и газа
Записанную систему дифференциальных уравнений целесообразно преобразовать к стандартному виду. Последовательная подстановка компонент тензора напряжения, выраженных через компоненты тензора скорости деформации (7.5), в уравнения движения (8.4) и затем кинематических соотношений между компонентами тензора скорости деформации и вектора скорости (7.4) после ряда математических преобразований приводит к уравнениям Навье52 – Стокса53:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂vx |
+ v |
|
|
|
|
|
∂vx |
|
|
+ v |
|
|
|
∂vx |
|
|
+ v |
|
∂vx |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
x ∂x |
y ∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z ∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= f |
|
|
|
|
1 ∂p |
|
|
|
λ |
|
|
|
|
|
∂2v |
|
|
|
|
|
|
∂2vy |
|
|
|
|
|
∂2v |
z |
|
|
|
|
∂2v |
|
|
|
∂2v |
|
|
|
∂2v |
|
|
|
|||||||||||||||||||||||||||||||
x |
|
− |
|
|
|
+ |
|
|
+ ν |
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ ν |
|
|
|
|
|
|
|
x |
+ |
|
|
|
|
x |
+ |
|
|
|
|
|
x |
|
, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
ρ ∂x |
|
|
ρ |
|
|
|
|
|
∂x |
2 |
|
|
|
|
|
∂x∂y ∂x∂z |
|
|
|
∂x |
2 |
|
|
∂z |
2 |
|
|
|
∂z |
2 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂vy |
+ v |
|
|
|
|
|
∂vy |
|
|
+ v |
|
|
|
∂vy |
+ v |
|
∂vy |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
x ∂x |
|
y ∂y |
|
|
z ∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= f |
|
− |
1 ∂p |
+ |
λ |
+ ν |
|
∂2v |
x |
|
+ |
|
∂2vy |
|
|
+ |
|
∂ |
2v |
z |
|
+ ν |
|
∂2vy |
|
+ |
|
∂2vy |
+ |
∂2vy |
|
|
, (10.1) |
|||||||||||||||||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
ρ ∂y |
|
ρ |
|
|
|
∂y∂x ∂y |
|
|
|
|
∂y∂z |
|
|
|
|
|
∂x |
|
|
|
|
|
|
∂z |
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂vz |
+ v |
|
|
|
|
|
∂vz |
|
|
+ v |
|
|
|
∂vz |
|
|
+ v |
|
∂vz |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
x ∂x |
|
|
|
|
|
y ∂y |
|
|
|
|
|
z ∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= f |
|
− |
1 ∂p |
+ |
λ + μ |
|
∂2v |
x |
|
|
|
+ |
∂2vy |
|
+ |
∂2v |
z |
|
+ |
μ ∂2v |
z |
+ |
∂2v |
z |
+ |
∂ |
2v |
z |
|
. |
|
|||||||||||||||||||||||||||||||||||||||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ρ ∂z |
|
|
|
ρ |
|
∂z∂x ∂z∂y |
|
|
|
|
|
|
∂z |
2 |
|
|
|
∂x |
2 |
|
|
|
|
∂z |
2 |
|
|
|
|
∂z |
2 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
В итоге получены три дифференциальных уравнения жидкой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(газовой) среды относительно трех компонент vx, vy и vz вектора скорости, давления p и плотности ρ рассматриваемой жидкости или газа.
52Навье Клод Луи Мари Анри (10.02.1785–21.08.1836) – французский механик и инженер, автор работ по строительной механике, сопротивлению материалов, теории упругости, гидравлике и гидромеханике.
53Стокс Джордж Габриель (13.08.1819–01.02.1903) – английский математик, механик, внес значительный вклад в гидро- и газодинамику, оптику и математическую физику. Президент Лондонского королевского общества.
110
