
книги / Математические и инструментальные методы комплексного оценивания сложных объектов в условиях неопределённости
..pdf3.1.Агрегирование двух критериев с точечными значениями
сиспользованием непрерывных ММКО
Произведём агрегирование двух критериев со значениями Xr = 1,3 и Xc 2,6. В этом случае мы можем использовать непрерывные ММКО. Тогда
|
X |
0,3; |
|
2 |
X |
0,6. |
1 |
|
r |
|
|
c |
Пусть матрица свёртки имеет элементы, которые показаны на рис. 3.2.
|
|
|
|
|
Хr |
|
4 |
3 |
3 |
2 |
4 |
|
3 |
3 |
2 |
1 |
3 |
|
3 |
2 |
2 |
1 |
2 |
|
3 |
2 |
1 |
1 |
1 |
Хc |
4 |
3 |
2 |
1 |
|
Рис. 3.2. Матрица свёртки, используемая для примеров (подразд. 3.1–3.8)
Тогда X |
1; |
X |
2; |
j m |
1; j |
m |
2; j |
m |
2; j |
m |
2. |
|
r |
|
c |
3 12 |
4 |
22 |
5 |
13 |
6 |
23 |
|
Согласно выражению (1.18), эквивалентному нечёткому ММКО с максиминным подходом, мы получим следующую комплексную оценку:
v X r , X c 1 0,3 2 2 0,6 2 1 1,6.
Согласно выражению (1.19), эквивалентному нечёткому ММКО с адди- тивно-мультипликативным подходом, мы получим следующую комплексную оценку:
v X r , X c 1 0,3 2 1 0,6 2 1 0,3 0,6 2 1 2 2 1,72.
3.2. Агрегирование двух критериев с интервалами значений
Произведём агрегирование двух критериев с интервалами значений X r 1,3;1,6 и X c 2,6;3,1 . В этом случае комплексная оценка будет также
представлена интервалом значений.
Пусть матрица свёртки имеет те же элементы, что показаны на рис. 3.2. Мы также можем использовать непрерывные ММКО, и нам необходимо определить только две комплексные оценки v Xr min Xr , Xc min Xc
и v Xr max Xr , Xc max Xc , потому что обе функции интерполяции (1.18) и (1.19) являются непрерывными и монотонными.
31

Нам известно, что v X r 1,3; X c 2,6 1,6 в случае использования максиминного подхода и v X r 1,3; X c 2,6 1,72 в случае использования ад- дитивно-мультипликативного подхода. Поэтому нам необходимо узнать
комплексную оценку только для случая v X r 1,6; Xc 3,1 . |
В этом случае |
||||||||||||||
|
X |
0,6; |
|
2 |
X |
|
0,1; |
X |
|
1; |
X |
3; |
j m |
2; j |
m 2; |
1 |
|
r |
|
|
c |
|
|
r |
|
|
c |
3 13 |
4 |
23 |
|
j5 m14 3; j6 m24 3. |
|
|
|
|
|
|
|
|
|
|
|||||
|
Согласно функции (1.18), в случае, когда 1 2 , необходимо использо- |
||||||||||||||
вать выражение j3 1 j4 |
j3 2 j6 |
j4 . Результат будет следующим: |
|||||||||||||
v X r , X c 2 0,6 2 2 0,1 3 2 2,1.
Согласно выражению (1.19) (в случае использования аддитивно-муль- типликативного подхода) мы получим ту же самую комплексную оценку:
v X r , X c 2 0,3 2 2 0,1 3 2 0,3 0,6 3 2 3 2 2,1.
Тогда комплексная оценка представляет собой интервал: в случае использования максиминного подхода v X r , X c 1,6;2,1 ; в случае использо-
вания аддитивно-мультипликативного подхода v X r , X c 1,72;2,1 .
3.3. Агрегирование двух критериев с точечными значениями с использованием нечётких ММКО
Рассмотрим тот же пример, как и в первом случае: Xr 1,3 и Xc 2,6 . Для
применения нечётких ММКО в данном случае каждое значение Xr и Xc необходимо представить в виде нечёткого числа, используя правило (2.1).
Согласно (2.1) критерии Xr 1,3 и Xc |
2,6 будут иметь вид |
|||||||||
Xr 1 / 0,7; |
2 / 0,3; 3 / 0;4 / 0 и Xc |
1 / 0; 2 / 0,4; 3 / 0,6; 4 / 0 . |
||||||||
В случае нечётких чисел каждому элементу матрицы соответствует пара |
||||||||||
значений функций принадлежности (рис. 3.3). |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
X r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4/0;0 |
3/0;0,6 |
3/0;0,4 |
|
2/0;0 |
|
4/0 |
|
|
|
|
3/0;0 |
3/0;0,6 |
2/0;0,4 |
|
1/0;0 |
|
3/0 |
|
|
|
|
3/0,3;0 |
2/0,3;0,6 |
2/0,3;0,4 |
|
1/0,3;0 |
|
2/0,3 |
|
|
|
|
3/0,7;0 |
2/0,7;0,6 |
1/0,7;0,4 |
|
1/0,7;0 |
|
1/0,7 |
|
|
X c |
4/0 |
3/0,6 |
2/0,4 |
1/0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.3. Матрица свёртки в нечётком виде |
|
||||||
|
|
при агрегировании критериев Xr |
1,3 и Xc 2,6 |
|
||||||
32

Для определения единственного значения функции принадлежности при максиминном подходе необходимо использовать теоретико-множе- ственную операцию пересечения (1.3) (рис. 3.4).
|
|
|
|
|
X r |
|
4/0 |
3/0 |
3/0 |
2/0 |
4/0 |
|
3/0 |
3/0 |
2/0 |
1/0 |
3/0 |
|
3/0 |
2/0,3 |
2/0,3 |
1/0 |
2/0,3 |
|
3/0 |
2/0,6 |
1/0,4 |
1/0 |
1/0,7 |
4/0 |
3/0,6 |
2/0,4 |
1/0 |
|
|
X c |
|
|
|
|
|
Рис. 3.4. Результат пересечения при использовании максиминного подхода
В этом случае (см. рис. 3.4) имеем три элемента матрицы с ненулевым значением функции принадлежности и одинаковым значением элемента матрицы: m13 = m22 = m23 = 2. Для элементов m22 и m23 значение функции принадлежности составляет 0,3, а для элемента m13 – 0,6. Тогда
v Xr , Xc 1/ 0,4; 2 / 0,3;0,6 ;3 / 0; 4 / 0 .
Для элемента с двумя значениями функции принадлежности 2 / {0,3 ;0,6} необходимо использовать теоретико-множественную операцию объединения (1.5) – максимум. Результат будет следующим:
v X r , Xc 1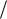 0,4; 2
0,4; 2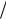 0,6; 3
0,6; 3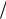 0; 4
0; 4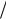 0 .
0 .
Согласно уравнению центра масс (1.8) комплексная оценка будет следующей:
v X r , X c |
1 0, 4 2 0, 6 3 0 4 0 |
1, 6. |
|
0, 4 0, 6 0 0 |
|||
|
|
В случае аддитивно-мультипликативного подхода матрица после выполнения операции пересечения (1.4) будет иметь вид (рис. 3.5):
v X r , Xc 1 0,28; 2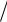 0,42;0,12;0,18 ; 3
0,42;0,12;0,18 ; 3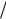 0; 4
0; 4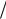 0 .
0 .
Согласно аддитивно-мультипликативному |
подходу для элемента |
2 / {0,42; 0,12; 0,18} необходимо использовать |
теоретико-множественную |
операцию суммирования (1.6). В этом случае результат комплексного оценивания будет следующим: v X r , Xc 1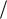 0,28; 2
0,28; 2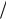 0,72; 3
0,72; 3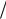 0; 4
0; 4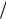 0 .
0 .
33

|
|
|
|
|
X r |
|
4/0 |
3/0 |
3/0 |
2/0 |
4/0 |
|
3/0 |
3/0 |
2/0 |
1/0 |
3/0 |
|
3/0 |
2/0,18 |
2/0,12 |
1/0 |
2/0,3 |
|
3/0 |
2/0,42 |
1/0,28 |
1/0 |
1/0,7 |
4/0 |
3/0,6 |
2/0,4 |
1/0 |
|
|
X c |
|
|
|
|
|
Рис. 3.5. Результат пересечения при использовании аддитивно-мультипликативного подхода
Действительно-значная комплексная оценка будет следующей:
v X r , X c 1 0, 28 2 0,72 3 0 4 0 1,72. 0, 28 0,72 0 0
3.4. Погрешность комплексной оценки
вслучае максиминного подхода к операциям (1.3) и (1.5) над нечёткими множествами
Пусть матрица свёртки имеет такие же элементы, как в примерах выше, а критерии имеют другой вид:
Xr 1 / 0,4;2 / 0,6;3 / 0;4 / 0 и Xc 1 / 0;2 / 0,3;3 / 0,7;4 / 0 . Каждому элементу матрицы в этом случае также соответствует два значения функций принадлежности (рис. 3.6).
|
|
|
|
|
X r |
|
4/0;0 |
3/0;0,6 |
3/0;0,4 |
2/0;0 |
4/0 |
|
3/0;0 |
3/0;0,6 |
2/0;0,4 |
1/0;0 |
3/0 |
|
3/0,3;0 |
2/0,6;0,7 |
2/0,6;0,3 |
1/0,3;0 |
2/0,6 |
|
3/0,7;0 |
2/0,4;0,7 |
1/0,4;0,3 |
1/0,7;0 |
1/0,4 |
4/0 |
3/0,7 |
2/0,3 |
1/0 |
|
|
X c |
|
|
|
|
|
Рис. 3.6. Матрица свёртки в нечётком виде при агрегировании критериев Xr 1,6; Xc 2,7
Используем функцию пересечения (1.3) (рис. 3.7).
В данном случае (см. рис. 3.7) имеем три элемента матрицы с ненулевым значением функции принадлежности и одинаковым значением элемента матрицы: m13 = m22 = m23 = 2. Для элемента m22 значение функции принадлежности равно 0,3, для элемента m23 – 0,6, а для элемента m13 – 0,4. Для элемента с тремя значениями функции принадлежности 2 / {0,3; 0,4; 0,6} используем теоретико-множественную операцию объединения (1.5). В этом случае ре-
зультат будет следующим: v X r , Xc 1 / 0,3;2 / 0,6;3 / 0;4 / 0 .
34

|
|
|
|
|
X r |
|
4/0 |
3/0 |
3/0 |
2/0 |
4/0 |
|
3/0 |
3/0 |
2/0 |
1/0 |
3/0 |
|
3/0 |
2/0,6 |
2/0,3 |
1/0 |
2/0,6 |
|
3/0 |
2/0,4 |
1/0,3 |
1/0 |
1/0,4 |
4/0 |
3/0,7 |
2/0,3 |
1/0 |
|
|
X c |
|
|
|
|
|
Рис. 3.7. Результат пересечения (1.3)
Согласно уравнению центра масс (1.8) комплексная оценка будет следующей:
v X r , X c |
1 0,3 2 0,6 3 0 4 0 |
|
1,5 |
1,67. |
|
0,3 0,6 0 0 |
0,9 |
||||
|
|
|
Элементы матрицы с ненулевыми значениями функции принадлежности имеют следующие значения: m12 = 1, m22 = 2, m13 = 2, m23 = 2, что соответствует стандартной функции F4 (см. §1, табл. 1.1). Если использовать (1.13), получим:
v Xr , Xc 1/ 1 0,7 ;2 / 0,7 .
Согласно выражению (2.1) такое нечёткое число после дефазификации будет числом, принадлежащим действительному множеству:
v X r , X c 1,7.
Согласно уравнению |
центра масс (1.8) |
нечёткие |
числа |
Xr 1/0,4;2/0,6;3/0;4/0 и |
Xc 1/0;2/0,3;3/0,7;4/0 |
примут |
значения |
Xr 1,6 и Xc 2,7. |
|
|
|
Используя непрерывную функцию (1.18), мы получим: v X r , X c 1 0,6 2 2 0,7 2 1 1,7.
3.5. Агрегирование двух критериев с Ф-нечёткими числами при аддитивно-мультипликативном подходе
Пусть матрица свёртки имеет такие же элементы, как в примерах выше, а критерии определяются как Ф-нечёткие числа (рис. 3.8):
Xr 1/ 0,3 0,4 ;2/ 0,4 0,5 ;3/ 0,1 0,2 ;4/ 0,1 0,2 ,
Xc 1/ 0,1 0,2 ;2/ 0,2 0,4 ;3/ 0,4 0,5 ;4/ 0,1 0,3 .
35

v X r , X c |
|
|
|
|
Xr |
Х r |
Х r |
|
|
|
|
|
|||||
|
|
4 |
3 |
3 |
2 |
4 |
0,1 |
0,2 |
|
|
3 |
3 |
2 |
1 |
3 |
0,1 |
0,2 |
|
|
3 |
2 |
2 |
1 |
2 |
0,4 |
0,5 |
|
|
3 |
2 |
1 |
1 |
1 |
0,3 |
0,4 |
Xc |
|
4 |
3 |
2 |
1 |
|
|
|
Х c |
0,1 |
0,4 |
0,2 |
0,1 |
|
|
|
|
Х |
c |
0,3 |
0,5 |
0,4 |
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.8. Матрица свёртки в Ф-нечётком виде
Такой случай может соответствовать ситуации, когда в качестве лиц, привлечённых к процедуре оценки частных критериев, выступают не эксперты, а, например, рядовые носители предметно-профессиональной области, или в отношении частных критериев имеется существенная неопределённость, которая не позволяет эксперту высказаться категорически, и даже его модальные суждения носят весьма размытый характер.
В случае Ф-нечёткого комплексного оценивания используется алгоритм 38, приведённый в §1.
Рассмотрим, например, элемент (2;2) – m22.
Векторы значений функции принадлежности будут следующими:
–первый: 22 0,5; 0,4; 0,9; 0,7; 0,6; 0,9 ;
–второй: 22 0,4; 0,2; 0,8; 0,6; 0,5; 0,8 .
Если использовать умножение в качестве операции пересечения (1.4),
то 22 0,5 0,4 0,9 0,7 0,6 0,9 0,068, |
|
22 |
|
0, 4 0, 2 0,8 0,6 0,5 0,8 |
|
|
|
|
0,015. Тогда m22 2/ 0,015;0,068 .
Аналогично применим предложенный подход ко всем элементам матрицы (рис. 3.9).
Выполнив операцию объединения путём суммирования минимальных и максимальных значений при одинаковых элементах матрицы свёртки, получим следующую Ф-нечёткую комплексную оценку:
v 1 / |
|
0,035; 0,052 |
|
; 2 / |
|
0,080; 0,319 |
|
; |
|
|
|
|
|
|
|
|
|
3 / 0,046; 0,262 ; 4 / 0,004; 0,032 |
. (3.1) |
||||||
38 См. выражения (1.15) – (1.17).
36

v X r , X c |
|
|
|
Xr |
Х r |
Х r |
|
|
|
|
|||||
|
4/[0,004; 0,032] |
3/ [0,013; 0,065] |
3 / [0,006; 0,039] |
2 / [0,005; 0,029] |
4 |
0,1 |
0,2 |
|
3/[0,002; 0,019] |
3/ [0,007; 0,039] |
2 / [0,003; 0,023] |
1 / [0,002; 0,017] |
3 |
0,1 |
0,2 |
|
3/[0,010; 0,057] |
2/ [0,032; 0,113] |
2 / [0,015; 0,068] |
1 / [0,012; 0,050] |
2 |
0,4 |
0,5 |
|
3/[0,008; 0,043] |
2/ [0,025; 0,086] |
1 / [0,012; 0,052] |
1 / [0,009; 0,038] |
1 |
0,3 |
0,4 |
Xc |
4 |
3 |
2 |
1 |
|
|
|
Х c |
0,1 |
0,4 |
0,2 |
0,1 |
|
|
|
Х |
0,3 |
0,5 |
0,4 |
0,2 |
|
|
|
|
|
|
|
||||
c
Рис. 3.9. Матрица свёртки в Ф-нечётком виде, где элементы матрицы получены с помощью аддитивно-мультипликативного подхода
Такую Ф-нечёткую комплексную оценку условно можно представить в виде двух нечётких множеств, построенных по предложенному ранее алгоритму 39, и после их пересечения получим:
v 1 / 0,045;2 / 0,292;3 / 0,232;4 / 0,027 . |
(3.2) |
Это нечёткое множество путём дефазификации (1.8) можно представить в виде числа на множестве действительных значений:
v |
1 0,045 2 0, 292 3 0, 232 |
4 0,027 |
|
1, 433 |
2, 40. |
|
0,045 0, 292 0, 232 0, |
027 |
0,596 |
||||
|
|
|
Отметим, что при Ф-нечётком комплексном оценивании сумма значений функций принадлежности может не принимать значение единицы. Поэтому требовать выполнения этого условия от выражения (3.2), полученного из Ф-нечёткого числа (3.1), непрактично.
3.6. Агрегирование двух критериев с Ф-нечёткими числами при максиминном подходе
Пусть матрица свёртки имеет такие же элементы, как в примерах выше, а критерии определяются как Ф-нечёткие числа (см. рис. 3.8). Используя операцию пересечения (1.3) и применяя выражения (1.15)–(1.17), получим, что элемент (2;2) будет следующим: m22 2 / 0,2;0,4 . Аналогично определя-
ются все элементы с использованием операции пересечения (1.3) – минимум
(рис. 3.10).
39 См. §1, выражения (1.15), (1.16).
37

v X r , X c |
|
|
|
Xr |
Х r |
Х r |
||
|
|
|
||||||
|
|
4 / [0,1; 0,2] |
3 / [0,1; 0,2] |
3 / [0,1; 0,2] |
2 / [0,1; 0,2] |
4 |
0,1 |
0,2 |
|
|
|
|
|
|
3 |
0,1 |
0,2 |
|
|
3 / [0,1; 0,2] |
3 / [0,1; 0,2] |
2 / [0,1; 0,2] |
1 / [0,1; 0,2] |
|||
|
|
|
|
|
|
2 |
0,4 |
0,5 |
|
|
3 / [0,1; 0,3] |
2 / [0,4; 0,5] |
2 / [0,2; 0,4] |
1 / [0,1; 0,2] |
|||
|
|
|
|
|
|
1 |
0,3 |
0,4 |
|
|
3 / [0,1; 0,3] |
2 / [0,3; 0,4] |
1 / [0,2; 0,4] |
1 / [0,1; 0,2] |
|||
|
|
|
|
|
|
|
|
|
Xc |
|
4 |
3 |
2 |
1 |
|
|
|
|
Х c |
0,1 |
0,4 |
0,2 |
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х c |
0,3 |
0,5 |
0,4 |
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.10. Матрица свёртки в Ф-нечётком виде, где элементы матрицы получены с помощью максиминного подхода
В случае максиминного подхода Ф-нечёткая комплексная оценка будет следующей:
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 / |
|
0,2; 0,4 |
|
; 2 / |
|
0,3; 0,5 ; |
3 / |
|
0,1; 0,3 ; 4 / |
|
0,1; 0,2 |
. |
Нечёткое число получим аналогично:
v 1 / 0,4; 2 / 0,5; 3 / 0,2; 4 / 0,2 .
Наконец, аналогично комплексную оценку представим как действительное число:
v |
1 0, 4 2 0,5 3 0, 2 |
4 0, 2 |
|
2,8 |
2,15. |
|
0, 4 0,5 0, 2 0, |
2 |
1,3 |
||||
|
|
|
3.7. Комплексное оценивание с распределением вероятностей значений частных критериев
Пусть матрица свёртки имеет такие же элементы, как в примерах выше, а для частных критериев Xr = {1, 2, 3, 4} и Xс = {1, 2, 3, 4} имеются следующие распределения вероятностей состояний:
P(Xr) = {0,1; 0,2; 0,4; 0,3}, P(Xc) = {0,2; 0,3; 0,3; 0,2}.
Тогда матрицу свёртки можно представить так, как показано на рис. 3.11. Вероятность того, что комплексной оценкой будет элемент, находящийся на пересечении строки r и столбца c, будет определяться произведе-
нием вероятностей P(Xr = r) и P(Xc = c):
P(Х= mrc(Xr, Xc))=P(Xr)·P(Xc).
38
|
|
|
|
|
Xr |
P(Xr) |
|
4 |
3 |
3 |
2 |
4 |
0,3 |
|
3 |
3 |
2 |
1 |
3 |
0,4 |
|
3 |
2 |
2 |
1 |
2 |
0,2 |
|
3 |
2 |
1 |
1 |
1 |
0,1 |
Xс |
4 |
3 |
2 |
1 |
|
|
P(Xс) |
0,2 |
0,3 |
0,3 |
0,2 |
|
|
Рис. 3.11. Матрица свёртки при наличии распределения вероятностей значений частных критериев
Далее для упрощения записи обозначим P(Х = mrc(Xr, Xc)) как Prc. Поскольку элементы матрицы образуют полную группу событий того,
какая оценка будет комплексной, и они не являются связными, то вероятность того, что комплексной оценкой будет значение 1, 2, 3 или 4, будет определяться суммой вероятностей соответствующих элементов:
P(Х = 1) = P11 + P12 + P21 + P31 = 0,02 + 0,03 + 0,04 + 0,08 = 0,17;
P(Х = 2) = P13 + P22 + P23 + P32 + P41 = 0,03 + 0,06 + 0,06 + 0,12 + 0,06 = 0,33;
P(Х = 3) = P14 + P24 + P33 + P34 + P42 +P43 =
= 0,02 + 0,04 + 0,12 + 0,08 + 0,09 + 0,09 = 0,44; P(Х = 4) = P44 = 0,06.
Таким образом, P(X(P(Xr), P(Xc))) = {0,17; 0,33; 0,44;0,06}.
3.8. Сравнение комплексного оценивания с распределением вероятностей значений частных критериев и непрерывного и нечёткого аддитивно-мультипликативного оценивания
Поскольку ранее утверждалось, что подход к комплексному оцениванию с распределением вероятностей значений частных критериев является эквивалентным аддитивно-мультипликативной процедуре нечёткого комплексного оценивания, то целесообразно сравнить эти подходы, а также целесообразно сравнение с непрерывным подходом, эквивалентным адди- тивно-мультипликативной процедуре нечёткого комплексного оценивания, с целью разъяснения разницы в их применении.
Пусть сворачиваемые критерии и результат комплексного оценивания имеют распределения вероятностей, как в примере 3.7.
39

Для получения комплексной оценки на множестве действительных значений в виде скаляра можно условно воспользоваться «взвешиванием» 40, где весовой коэффициент соответствует вероятности того, что комплексной оценкой будет значение {1, 2, 3, 4}, что соответствует математическому ожиданию E(P(X)).
Тогда E(P(X(P(Xr), P(Xc)))) = 2,39.
Если взять математическое ожидание по критериям Xr и Xc:
E(P(Xr)) = 2,9, E(P(Xc)) = 2,5;
и свернуть с помощью непрерывной функции интерполяции (1.19), то полу-
чится результат: X(E(P(Xr)), E(P(Xc))) = 2,45.
Если результаты математического ожидания представить в виде нечётких чисел согласно выражению (2.1):
X r (E(P(Xr))) = {1 / 0; 1 / 0,1; 3 / 0,9; 4 / 0}; X c (E(P(Xс))) = {1 / 0; 1 / 0,5; 3 / 0,5; 4 / 0};
и свернуть с помощью процедуры нечёткого комплексного оценивания, эквивалентной на треугольных нечётких множествах 41 непрерывной функции интерполяции, то получится также отличающийся результат:
X ( X r (E(P(Xr))); X c (E(P(Xс)))) = {1 / 0; 2 / 0,55; 3 / 0,45; 4 / 0}.
Приведя этот результат к множеству действительных значений с помощью центра масс 42, получим оценку:
X ( X r (E(P(Xr))); X c (E(P(Xс)))) → X R1= 2,45,
аналогичную полученной при непрерывном подходе.
Как видно из обоих примеров, приведённых выше, результат математического ожидания комплексной оценки с распределением вероятностей не совпадает с результатами комплексного оценивания, полученными по математическому ожиданию распределений вероятностей сворачиваемых критериев.
Дело в том, что сворачивать результаты математического ожидания распределений вероятностей в общем случае не правильно. Только в частном случае, если бы распределения вероятностей состояний частных критериев были аналогичны функциям принадлежностей:
P(Xr) = {0; 0,9; 0,1; 0}, P(Xc) = {0; 0,5; 0,5; 0},
результаты бы совпали.
40См. работу [34, с. 57].
41См. §2, рис. 2.1.
42См. §1, выражение (1.8).
40
