книги / Методы вычислительной математики

Согласно методу Ньютона строится итерационная процедура

x(s+1) = x(s) − f (x(s) )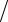 fx′(x(s) ).

Поскольку fx′(x)= 2 + cos(x), формула метода Ньютона принимает вид

цесс сходится. Результаты расчетов приведены в табл. 3.3.

Модификации метода Ньютона

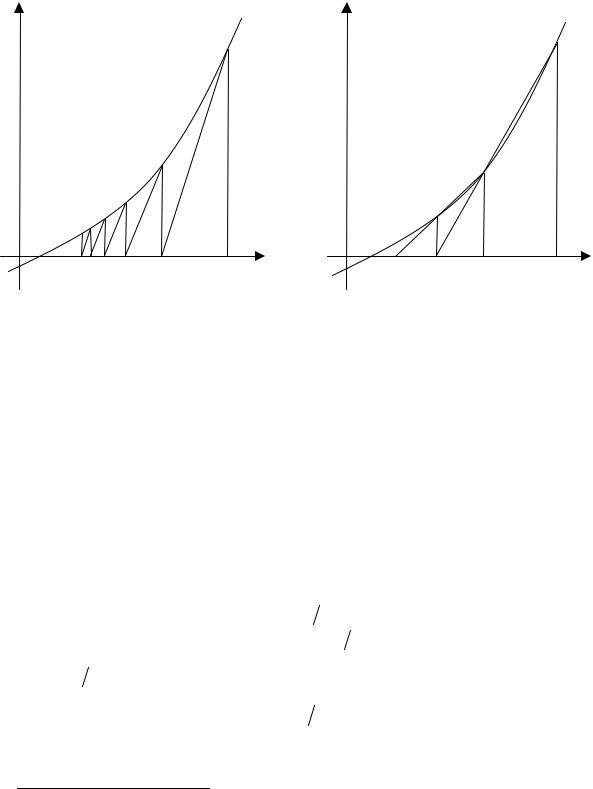
Одна из модификаций метода Ньютона заключается в том, что производная функции f(x) определяется только один раз для начальной точки x0 итерационного процесса (рис. 3.5, а):

x(s+1) = x(s) − f (x(s) )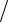 fx′(x(0) ).

При таком способе решения уравнения скорость сходимости уменьшается, иногда существенно. Эту модификацию метода целесообразно применять в том случае, когда вычисление производной связано с большими затратами вычислительных ресурсов (времени, оперативной памяти), либо когда аналитический вид функции f(x) неизвестен, что часто бывает при решении прикладных инже-

81

нерных задач. Кроме того, практически всегда можно подобрать начальное значение x(0) таким образом, что f ′(x(0) )≠ 0 , то есть не будет аварийной остановки вычислительного алгоритма.

Рис. 3.5. Схемы модифицирования метода Ньютона: a – с начальным значением касательной; б – метод секущих

Другая модификация (метод секущих) заключается в замене производной

функции f(x) ее разностным аналогом (рис. 3.5, б):

x(s+1) = x(s) − f (x(s) )(x(s) − x(s−1) )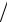[f (x(s) )− f (x(s−1) )] .

В этом случае получена двухточечная схема, то есть для начала расчетов необходимо задать две начальные точки: x(0) и x(1) .

Возможно, что на заданном отрезке может оказаться несколько корней. В этом случае итерационный процесс позволит вычислить какой-то один корень уравнения. Для отделения корней в некоторых случаях можно воспользо-

1 Лопиталь Гийом Франсуа Антуан де [1661 – 1704] – французский математик, автор первого печатного учебника по дифференциальному исчислению.

82

при условии ограниченности значения производной функции, то есть в случае

3.4. Система нелинейных уравнений

Рассматривается система m нелинейных алгебраических уравнений

В общем случае итерационные методы решения системы нелинейных алгебраических уравнений могут быть представлены в канонической форме

3.4.1. Метод простых итераций

Из выражения (3.10) можно получить систему линейных алгебраических уравнений относительно искомых неизвестных:

B(s+1) X (s+1) = B(s+1) X (s) − τ(s+1) F(X (s) ).

83

В частном случае стационарного итерационного метода, когда B(s+1) = B = const, τ(s+1) = τ = const, последнее соотношение преобразуется к итерационному выражению

X (s+1) = X (s) − τB−1F(X (s) ).

Иначе говоря, исходная итерационная процедура сводится к схеме метода простых итераций:

Φ(x2 ) − Φ(x1 ) ≤ Cx2 − x1 .

Теорема 3.3. Пусть на множестве A = {X Rm X −a ≤ r} определен сжи-

мающий оператор Φ с коэффициентом сжатия С, причем

Φ(a)− a ≤ (1 − C)r, 0 < C <1.

Φ ~

Тогда в А оператор имеет единственную неподвижную точку X , итера-

3.4.2. Метод релаксации

Если в выражении (3.11) матрица В = Е, то есть является оператором тождественного преобразования, тогда Φ(X (s) )= X (s) − τF(X (s) ) и метод сходится, если Φ′(X ) <1 X A. В рассматриваемом случае

84

(1− 1− 2H )S 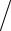H ≤ r.

Тогда:

–в заданном шаре радиуса r уравнение F(X )= 0 имеет решение;

–в вычислительном процессе Ньютона (3.12) приближение X (s) может

t(s) – приближение к нему, построенное при начальном приближении t(0) = 0. Доказательство теоремы 3.4 приведено в книге [24]. В качестве модифика-

итерационный процесс строится так, что из каждого уравнения системы определяется значение только одной неизвестной xi(s+1) , а значения остальных берутся с предыдущего шага,

производится с помощью какого-либо известного метода решения нелинейного уравнения с одной неизвестной.

3.4.5. Нелинейный вариант метода Зейделя

В отличие от метода Якоби, при определении на s +1 итерации i-й неизвестной xi(s+1) используются уже найденные на этой же итерации значения предыдущих неизвестных xk(s+1) , k =1,i −1:

86

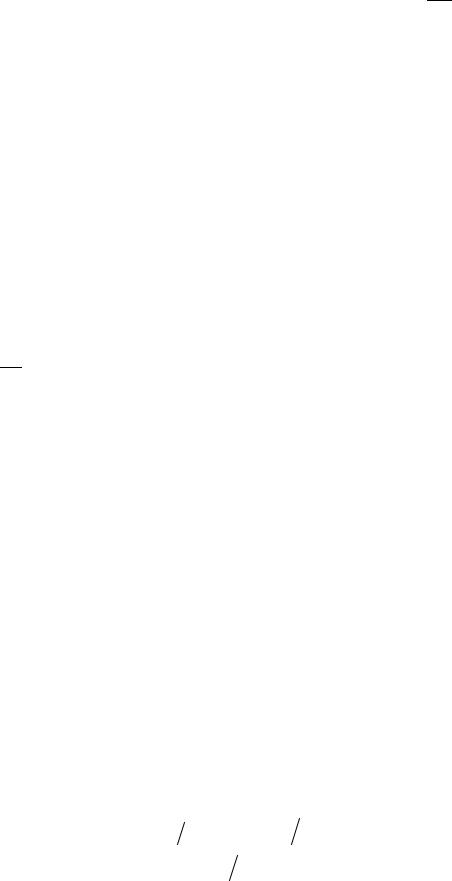
f (x(s+1) , x(s+1) ,…, x(−s+1) , x(s+1) , x(+s) ,…, x(s) )= 0, i =1,m . i 1 2 i 1 i i 1 m

Определение искомой величины xi(s+1) на очередной итерации производится, как и в методе Якоби, с помощью любого известного метода решения нелинейного уравнения с одной неизвестной.

Пример 3.4. Решить систему нелинейных алгебраических уравнений

Эта система нелинейных уравнений имеет четыре пары корней: x1 =1,338390, x2 =1,791288;

x1 = −1,338390, x2 =1,791288; x1 =1,670715i, x2 = 2,791288; x1 = −1,670715i, x2 = 2,791288;

где i = −1 – комплексная единица. Для отыскания корней уравнений этой системы используется метод Ньютона:

87

Результаты вычисления корней заданного уравнения методом Ньютона приведены в табл. 3.4.

Контрольные вопросы и задания

3.1.Сформулируйте задачу о нахождении корней нелинейного уравнения.

3.2.Опишите метод половинного деления для вычисления корней нелинейного уравнения. Поясните геометрический смысл метода половинного деления.

3.3.Опишите метод простых итераций для вычисления корней нелинейного уравнения. Поясните геометрический смысл этого метода.

3.4.Сформулируйте критерии остановки итерационного вычислительного процесса при определении корней нелинейного уравнения. Сходимость (расходимость) итерационного решения.

3.5.Сформулируйте условия сходимости метода простых итераций для одного нелинейного уравнения.

3.6.Опишите метод Ньютона для вычисления корней нелинейного уравне-

ния.

3.7.Поясните геометрический смысл метода Ньютона.

3.8.Сформулируйте условия сходимости метода Ньютона для нелинейного уравнения.

88

3.9.Приведите возможные модификации метода Ньютона для определения корней нелинейного уравнения.

3.10.Применение метода простых итераций для решения системы нелинейных уравнений.

3.11.Сформулируйте условия сходимости метода простых итераций для системы нелинейных уравнений.

3.12.Поясните порядок применения метода Ньютона для решения системы нелинейных уравнений.

3.13.Сформулируйте условия сходимости метода Ньютона для системы нелинейных уравнений.

3.14.Опишите решение системы нелинейных уравнений методом Якоби.

3.15.Опишите решение системы нелинейных уравнений методом Зейделя.

89

4. АППРОКСИМАЦИЯ ФУНКЦИЙ

Под аппроксимацией заданной функции f (x) понимается выбор функции ϕ(x) из некоторого определенного класса (например, среди алгебраических многочленов заданной степени), в том или ином смысле близкой к f (x) и даю-

щей ее приближенное представление.

Для решения ряда прикладных задач возникает необходимость приближенной замены функции f (x) некоторым набором известных функций, вычис-

ление которых проще организовать.

Вчастности, может рассматриваться задача о наилучшем приближении

внормированном пространстве Н, когда заданную функцию f H требуется

заменить линейной комбинацией известных элементов ϕk H , k = 0,m , так, чтобы отклонение

m

f − ∑ ak ϕk

k=0

было минимальным.

Частный случай аппроксимации функции – задача интерполирования – состоит в том, чтобы функцию f (x), известную лишь в узлах некоторой сетки на

заданном отрезке, то есть определенную в виде таблицы, f (xi )= fi , i = 0,n , приблизить непрерывной на этом отрезке функцией ϕ(x), которая в точках xi совпадает с заданными табличными значениями,

k=0

где ϕk (x) – набор линейно независимых функций, например, полиномов:

ϕ(x) = a0 + a1x + a2 x2 +…+ am xm .

Очевидно, что в задачах о наилучшем приближении и интерполировании функция ϕ(x) определяется набором параметров ak , k = 0,m , от которых зави-

сит линейно. В противном случае говорят о нелинейной аппроксимации.

Если число узлов n, в которых задана функция f (x), совпадает с числом m

функций, то есть n = m, формулы (4.1) и (4.2) позволяют получить систему линейных алгебраических уравнений

90