книги / Методы вычислительной математики

новы программирования на алгоритмических языках высоко уровня, знать современные технологии разработки и создания программных продуктов, владеть навыками отображения числовой информации. Знание возможностей ЭВМ, основ алгоритмизации, программирования и технологий создания математических моделей является одним из ключевых этапов в подготовке специалиста, способного в полной мере использовать возможности вычислительной техники в области своей профессиональной деятельности.

Использование в учебном процессе технического университета современных способов решения практически важных прикладных задач позволяет целенаправленно сформировать в сознании будущего специалиста представление о том, что вычислительная техника является точным и мощным инструментом бакалавра, инженера, магистра, ученого, многократно усиливающим интеллектуальный и творческий потенциал исследователя.

Последовательное и детальное изучение научных основ современных методов вычислительной математики и их приложений к решению актуальных прикладных инженерных задач является неотъемлемой частью процесса формирования инновационной составляющей системы теоретических знаний и практических навыков выпускника современного высшего технического университета.

Настоящее пособие содержит последовательное изложение методов решения систем линейных алгебраических уравнений прямыми (Гаусса, квадратного корня) и итерационными (Якоби, Зейделя и другими) методами, нелинейных уравнений (методы Ньютона, половинного деления, простых итераций), аппроксимации функций (полиномы Ньютона, Лагранжа, сплайн-аппроксимация, методы наименьших квадратов и наилучшего приближения).

Рассматриваются способы построения разностных аналогов производных первого и второго порядков, а также методы вычисления приближенных значений определенных интегралов методами прямоугольников, трапеций и парабол. Одним из главных вопросов этого раздела является теоретическая оценка погрешности аппроксимации выбранной вычислительной схемой исходного дифференциального или интегрального соотношения. Изучаются способы оценки погрешности численного результата с использованием последовательности сгущающихся разностных сеток.

Для построения решений обыкновенных дифференциальных уравнений в задачах Коши и граничных задачах рассматриваются методы Эйлера, Рунге –

11

Кутты различных порядков, Адамса, пристрелки, сеточный, Галеркина, наименьших квадратов. Основная идея решения дифференциальных уравнений численными методами заключается, как правило, в сведении исходной дифференциальной задачи к системам алгебраических (линейных или нелинейных) уравнений. При этом, естественно, возникает вопрос о решении получаемых систем алгебраических уравнений одним из изученных ранее методов. Значительное внимание уделяется оценкам погрешностей аппроксимации разностными схемами исходных дифференциальных уравнений, позволяющим судить о степени адекватности используемых сеточных моделей исходной дифференциальной задаче. Подробно рассматриваются вопросы устойчивости вычислительных разностных схем и исследуются условия сходимости получаемых приближенных и численных решений к точным решениям поставленных задач.

Существенная часть учебного пособия посвящена методу моментов (взвешенных невязок), частными случаями которого оказываются многие известные методы решения задач математической физики: Галеркина, наименьших квадратов, подобластей, потоков, конечных и граничных элементов и целый ряд других. Следует отметить, что рассмотрение этих методов, как правило, выходит за рамки традиционных курсов вычислительной математики, и излагается в специальной литературе.

Метод конечных элементов является, по-видимому, одним из наиболее распространенных современных способов решения прикладных задач. Наглядность, простота и универсальность сделали его популярным среди специалистов, занятых решением инженерных задач. На основе метода конечных элементов созданы многие прикладные программные комплексы для решения конструкторских задач, возникающих в машиностроительной, авиационной, судостроительной, автомобильной промышленности.

Метод граничных элементов явился развитием идей, лежащих в основе метода конечных элементов. В этом методе конечные элементы используются для аппроксимации границы области, а аппарат классических интегральных уравнений применяется для отыскания решения внутри рассматриваемой области. Этот метод широко применяется для решения задач механики жидкостей и газа, упругости, вязкоупругости и пластичности, в численных исследованиях ряда важных научных и технических проблем.

12

ются законы, описывающие лишь интересующее исследователя поведение объекта. Например, при моделировании движения космического аппарата вне атмосферы Земли достаточно использовать уравнения классической механики и не учитывать его прочностные характеристики; при исследовании химических превращений вещества нет смысла учитывать упругие или пластические характеристики материала.

Следующий этап – математическая модель – представляет собой формализованную запись выбранных законов, описывающих поведение объекта, посредством абстрактных математических объектов и операций. В общем случае математическая модель включает запись систем уравнений (алгебраических, обыкновенных дифференциальных или в частных производных, интегральных, интегро-дифференциальных), неравенств, начальных и граничных условий.

Вслучае, если для записанной системы уравнений невозможно получить точное1 решение, используются соответствующие методы приближенного2 или численного3 решения с использованием вычислительной техники.

Программирование для электронных вычислительных машин представляет собой процесс подготовки кода, реализующего вычислительные алгоритмы численного решения задач на языках высокого уровня. Существуют специальные способы и подходы, технологии создания программных продуктов, гарантирующие подготовку компьютерных программ в заданные сроки с высоким качеством. К их числу относятся технологии структурного и объектноориентированного программирования.

Проведение расчетов и анализ результатов – этап, требующий значительных интеллектуальных усилий и навыков по обработке, представлению и осмыслению получаемых решений. Необходима интерпретация громадных объемов числовой информации в виде схем, диаграмм, графиков, таблиц, изолиний, рисунков, мультипликации и тому подобного. Основная цель этого этапа – установление степени адекватности численных результатов компьютерного моделирования данным натурных наблюдений и измерений.

Вслучае, если имеется существенное отклонение расчетных и экспериментальных данных, необходимо вернуться к исходному либо промежуточным этапам построения математической модели с целью уточнения законов, описы-

1Точным называется решение, полученное в элементарных функциях.

2Под приближенным понимается решение, получаемое в виде сходящейся последовательности (например, с использованием итерационных методов, рядов Фурье, Тейлора).

3Численное решение предполагает получение множества значений искомой функции для конечного числа узловых значений аргументов (методы конечных и граничных элементов, сеточные и другие).

14

вающих поведение объекта, выбора более приемлемого метода решения математической задачи, проверки правильности машинного кода программы. При получении достаточной степени достоверности получаемых численных результатов переходят к «промышленной» эксплуатации компьютерной модели.

Следует четко понимать, что целью математического моделирования является не столько описание известных закономерностей в поведении объекта, сколько предсказание его поведения в нестандартных ситуациях. Одно из основных направлений использования компьютерного моделирования – поиск оптимальных вариантов внешнего воздействия на объект с целью получения наивысших показателей результативности его функционирования: минимальная себестоимость, максимальная производительность, наибольшая прибыль, наименьшие затраты и потери и прочее.

1.1. Погрешность математической модели

Точность математической модели определяется правильностью принятых гипотез и упрощений, описывающих исследуемый объект. Оценка погрешности в этом случае может производиться только проверкой степени выполнения принятых гипотез при натурном наблюдении. Так, например, для моделирования поведения металла в процессах пластического деформирования, как правило, используют модели течения вязкой жидкости. Однако такое предположение может быть использовано лишь в процессах, проводящихся при достаточно высоких температурах.

Понятно, что погрешности этого рода являются неустранимыми в рамках принятых допущений и предположений. Повышение точности модели возможно при уточнении гипотез и законов, описывающих поведение исследуемого объекта: увеличение степеней свободы механизмов, повышение размерности задачи, отказ от грубых допущений. Это, как правило, приводит к повышению сложности систем уравнений и алгоритмов решения поставленной задачи.

1.2. Погрешность исходных данных

Любая математическая модель использует для проведения расчетов некоторые данные, получаемые с помощью натурных измерений. В силу погрешности измерительных инструментов, ошибок при снятии размеров, нестабильности свойств и размеров тел практически все исходные данные содержат погрешности, влияющие в большей или меньшей степени на результаты расчетов.

Погрешность определения параметров в промышленных условиях может достигать от 1 до 10 % . Точные исследования при наличии достаточной инструментальной базы и специальных условий позволяют достичь 0,001–0,0001 %

15

погрешности. Прецизионные измерения обеспечивают погрешность в пределах 10–8 –10–10 %. Как и в предыдущем случае, погрешности измерения вносят неустранимые искажения в результаты решения задач.

В связи с этим имеет смысл соотносить между собой точность выполнения математических вычислений и точность натурных измерений: погрешность расчетов на ЭВМ должна быть меньше погрешности, вносимой измерительными инструментами, на 1–2 порядка. Более высокая точность вычислений представляется нецелесообразной из-за погрешностей представления исходных данных.

1.3. Погрешность численного метода

Погрешность метода решения задачи на вычислительной машине определяется неточностью замены алгебраического, дифференциального или интегрального оператора в исходном уравнении поставленной задачи приближенным (нелинейного – линейным, дифференциального – разностным). Например, при замене интеграла конечной суммой площадей:

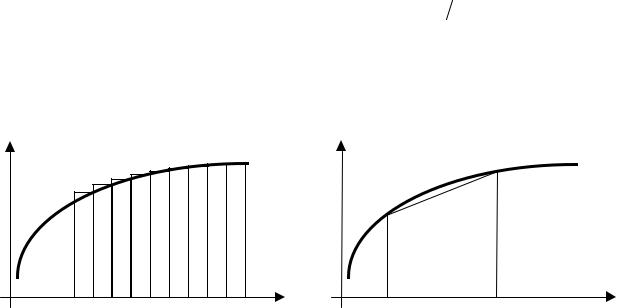
где n – число сегментов на отрезке [a, b], h – шаг интегрирования. Точное значение площади под графиком заданной функции заменяется суммой площадей аппроксимирующих прямоугольников (рис. 1.2, а).

f(x)

Очевидно, что при приближенном определении значения интеграла появляется погрешность, определяемая величиной «лишних» или «недостающих» частей взятых прямоугольников. Чем меньше шаг интегрирования h, тем меньше

16

PNRPU

погрешность вычисления значения интеграла. Аналогичная ситуация имеет место призаменепроизводнойфункции f (x) разностныманалогом(рис. 1.2, б):

df (x) ≈ f (x + h) − f (x) . dx h

Понятно, что в этом случае погрешность замены производной разностным аналогом также уменьшается с уменьшением величины шага h. Иначе говоря, при использовании численных методов погрешность решения является регулируемой: при корректном построении аппроксимации исходного уравнения всегда имеется некоторый параметр, варьированием которого можно регулировать величину погрешности получаемого результата.

Вместе с тем следует иметь в виду, что повышение точности решения модели приводит к ощутимому повышению затрат ресурсов ЭВМ (времени проведения вычислений и оперативной памяти). Поэтому необходимо придерживаться «золотой середины»: достижения приемлемых затрат вычислительных ресурсов при получении удовлетворительной точности решения задачи.

1.4. Погрешность проведения расчетов на ЭВМ

Оценка погрешности результата вычисления арифметического выражения при наличии ошибки в представлении данных может быть выполнена следующим образом. Пусть x – точное (как правило, неизвестное) значение, а ~x – приближенное значение некоторой величины. Абсолютная погрешность δ пред-

ставления x приближенным значением ~x определяется разностью

δ = ~x − x .

Поскольку точное значение x неизвестно, вводится «верхняя» оценка для погрешности: δ ≤ . Определяется величина относительной погрешности ε:

В приведенном выражении абсолютная погрешность делится на приближенное значение ~x , поскольку точное значение величины x неизвестно.

1.4.1. Погрешности округления чисел в ЭВМ

Округлением называется операция замены заданного числа x другим числом ~x , первые S значащих цифр которого совпадают с соответствующими цифрами исходного числа x, а начиная с S + 1 разряда содержат нули.

Округление чисел в ЭВМ в большинстве выполняется простым отбрасыванием (для сокращения числа выполняемых операций) «лишних» разрядов,

17

хотя возможны варианты, при которых в «младший» разряд округленного числа, в зависимости от ситуации, может добавляться единица.

Например, x = 0,123456789, тогда при S = 7 округленное число принимает значение ~x = 0,123456700. В этом случае модуль погрешности операции округ-

ления равен δ = x − x = 0,000000089 < 0,000000100 =10−7 , то есть не превышает единицы (с соответствующим порядком) в младшем разряде округленного числа. В рассмотренном примере =10−7 =10−S .

Вещественные числа в компьютере представляются в нормализованном виде: x = a pb , где a – мантисса (вещественное число), p – основание (целое число), b – показатель степени (целое число). Погрешности округления появляются при хранении именно мантиссы вещественного числа. Для определенности и однозначности представления чисел в ЭВМ принимается: p = 10 , 0,1 ≤ a <1,0 . При таком предположении в представлении чисел на персональных компьютерах IBM достоверными оказываются 6–7 значащих цифр1 (для хране-

ния вещественного числа используются 4 байта оперативной памяти).

При S = 7 округленное число представляется в виде ± 0, XXXXXXX 10b ,

где под символом X понимается любая цифра от 0 до 9. Модуль абсолютной погрешности определяется значением

Необходимо подчеркнуть, что для всех чисел, представимых в электронновычислительной машине, относительная погрешность одна и та же, что очень существенно для получения оценок погрешностей математических моделей.

1.4.2. Погрешности результатов арифметических операций

18

Погрешность результата сложения двух чисел, заданных с ошибкой, оценивается следующим образом:

Аналогично определяется погрешность результата вычитания:

Для определения абсолютных погрешностей операций умножения и деления двух чисел проводятся соответствующие выкладки:

Относительные погрешности операций умножения и деления:

ε = [(~x1~x2 )− (x1x2 )]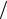~x1~x2 = (δ1~x2 + δ2 ~x1 − δ1δ2 )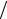~x1~x2 =

= δ1 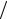~x1 +δ2 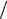~x2 −δ1δ2 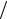~x1~x2 ≈ ε1 + ε2 ,

ε = (~x1 ~x2 − x1 x2 )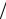(~x1 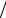~x2 ) = (~x2δ1 ~x1~x2 − ~x1δ2 ~x1~x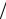2 )(1−δ2 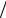~x2 ) =

=(ε1 −ε2 )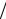(1−ε2 ) ≈ ε1 −ε2 .

Впоследних выражениях учитывается, что ε1, ε2 <<1.

Таким образом, при выполнении арифметических операций сложения (вычитания) складываются (вычитаются) абсолютные погрешности, а при умножении и делении – относительные погрешности.

1.4.3. «Потеря порядка» и «переполнение» при проведении вычислений на ЭВМ

Вводятся обозначения: ω – наименьшее положительное и Ω – наибольшее положительное числа, представимые в ЭВМ2.

Действительные числа из интервала − ω< x < ω нельзя представить в ЭВМ

внормализованном виде («потеря порядка»). В этом случае приближенное зна-

1При использовании вещественных переменных длиной 8 байт достоверными считаются 15 цифр; 19 цифр – при использовании вещественных переменных длиной 10 байт.

19

1.4.4. Машинная реализация вычислений

Рассматривается задача об оценке погрешности вычисления произведе-

1000

ния ∏ai . В соответствии с определением относительной погрешности при-

ближенный (округленный) результат произведения двух первых чисел в указанном выражении может быть оценен формулой (a1a2 )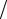(1 − ε). Для получения значения всего выражения следует многократно повторить эту операцию:

Для ε =10−6 значение выражения (1 − ε)−999 равно 1,0009995, что соответствует относительной погрешности вычисления всего результата 0,09985 %. Вычисления показывают, что при перемножении 1 000 000 сомножителей погрешность, рассчитанная аналогичным образом, может превысить 63 %. На практике такого катастрофического нарастания погрешности, как правило, не наблюдается в силу того, что погрешности округления имеют разные знаки и, следовательно, компенсируют друг друга.

Контрольные вопросы и задания

1.1.Дайте определение понятий математическая модель, вычислительный эксперимент, алгоритм, компьютерное моделирование.

1.2.Опишите этапы выполнения вычислительного эксперимента.

20